福建省福州市闽侯县2019-2020学年八年级下学期数学期中考试试卷

试卷更新日期：2021-04-27 类型：期中考试

进入出卷网下载

一、单选题

1. 在二次根式 $\sqrt{x - 2}$ 中，字母x的取值范围是（）

A、 $x > 2$ B、 $x < 2$ C、 $x \geq 2$ D、 $x \leq 2$

查看试题解析
2. 下列式子是最简二次根式的是（　　）

A、 $\sqrt{\frac{1}{3}}$ B、 $\sqrt{4}$ C、 $\sqrt{9}$ D、 $\sqrt{3}$

查看试题解析
3. 下列运算结果正确的是（）

A、 $\sqrt{{(- 3)}^{2}}$ ＝﹣3 B、(﹣ $\sqrt{2}$ )²＝2 C、 $\sqrt{6}$ ÷ $\sqrt{3}$ ＝2 D、 $\sqrt{16}$ ＝±4

查看试题解析
4. 以下列各组线段为边长，能构成直角三角形的是（　　）

A、1，1， $\sqrt{3}$ B、3，4，5 C、5，10，13 D、2，3，4

查看试题解析
5. 下面在函数y＝3x的图象上的点是（）

A、(1，3) B、(3，1) C、(3，3) D、(1，1)

查看试题解析
6. 在Rt△ABC中，若斜边AB＝3，则AC²+BC²等于(　　)

A、6 B、9 C、12 D、18

查看试题解析
7. 下列说法正确的是（　　）

A、对角线互相垂直的四边形是菱形 B、矩形的对角线互相垂直 C、一组对边平行的四边形是平行四边形 D、四边相等的四边形是菱形

查看试题解析
8. 一次函数 $y = - 2 x + 3$ 的图象经过（）

A、第一、二、三象限 B、第二、三、四象限 C、第一、三、四象限 D、第一、二、四象限

查看试题解析
9. 如图，在矩形COED中，点D的坐标是(1，3)，则CE的长是（）

A、3 B、 $2 \sqrt{2}$ C、 $\sqrt{10}$ D、4

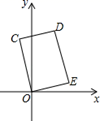查看试题解析
10. 如图所示，DE为△ABC的中位线，点F在DE上，且∠AFB=90°，若AB=6，BC=10，则EF的长为（）

A、1 B、2 C、3 D、5

查看试题解析

二、填空题

11. 在▱ABCD中， ∠A＝120°，则∠C＝.

查看试题解析
12. 命题“同位角相等，两直线平行”的逆命题是：．

查看试题解析
13. 在湖的两侧有A，B两个消防栓，为测定它们之间的距离，小明在岸上任选一点C，并量取了AC中点D和BC中点E之间的距离为16米，则A，B之间的距离应为米.

查看试题解析
14. 如图，在 $▱ A B C D$ 中，已知 $A D = 8 c m$ ， $A B = 6 c m$ ， $D E$ 平分 $∠ A D C$ ，交 $B C$ 边于点E，则 $B E =$ $c m$ ．

查看试题解析
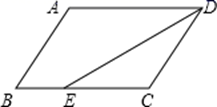15. 如图，直线l：y＝kx +b与y轴的交点是(0，－3)，当x＜0时，y的取值范围是.

查看试题解析
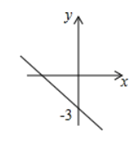16. 已知，在 $Δ A B C$ 中， $A B = 15 ， A C = 13$ ，且 $B C$ 边上的高为12，边BC的长为．

查看试题解析

三、解答题

17. 计算：

(1)、4 $\sqrt{5}$ + $\sqrt{45}$ ﹣ $\sqrt{20}$ ；

(2)、（2 $\sqrt{3} + \sqrt{6}$ ）（2 $\sqrt{3} - \sqrt{6}$ ）

查看试题解析
18. 如图，已知▱ABCD中，AE平分∠BAD ， CF平分∠BCD ，分别交BC、AD于E、F ．求证：DF=BE ．

查看试题解析
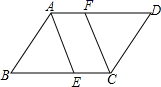19. 某天早晨，王老师从家出发步行前往学校，途中在路边一饭店吃早餐，如图所示是王老师从家到学校这一过程中的所走路程s（米）与时间t（分）之间的关系．

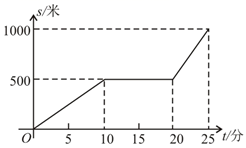(1)、学校离他家米，从出发到学校，王老师共用了分钟；王老师吃早餐用了分钟？

(2)、观察图形直接回答王老师吃早餐以前的速度快还是吃完早餐以后的速度快？

(3)、求出王老师吃完早餐后的平均速度是多少？

查看试题解析
20. 我国古代数学著作《九章算术》中的一个问题．原文是：今有池方一丈，葭生其中央，出水尺．引葭赴岸，适与岸齐问水深、葭长各几何译文大意是：如图，有一个水池，水面是一个边长为10尺的正方形，在水池正中央有一根芦苇，它高出水面1尺．如果把这根芦苇拉向水池边的中点，它的顶端恰好到达池边的水面．问水的深度与这根芦苇的长度分别是多少？

查看试题解析
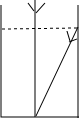21. 如图，直角坐标系中的网格由单位正方形构成，△ABC中，A点坐标为(2，3)，B点坐标为(－2，0)，C点坐标为(0，－1).

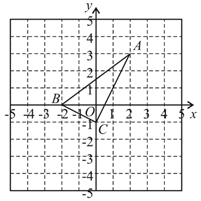(1)、求AC的长；

(2)、求证：AC⊥BC.

查看试题解析
22. 如图，一次函数y=kx+b的图象经过（2，4）、（0，2）两点，与x轴相交于点C．求：

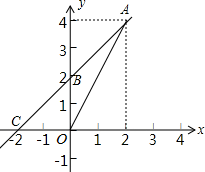(1)、此一次函数的解析式；

(2)、△AOC的面积．

查看试题解析
23. 根据要求作图.

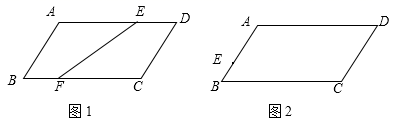(1)、如图1，平行四边形ABCD，点E，F分别在边AD，BC上，且AE＝CF，连接EF.请你只用无刻度直尺画出线段EF的中点O.（保留画图痕迹，不必说明理由）.

(2)、如图2，平行四边形ABCD，点E在边AB上，请你只用无刻度直尺在边CD上找一点F，使得四边形AECF为平行四边形，并说明理由.（注意：无刻度直尺只能过点画线段或直线或射线）.

查看试题解析
24. 在矩形ABCD中，AB＝3，AD＝4，将△ABD沿着BD折叠，使点A与点E重合.

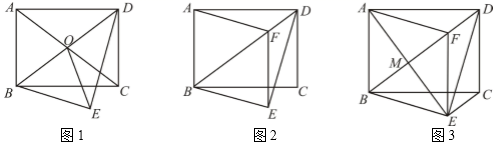(1)、如图，对角线AC、BD相交于点O，连接OE，则线段OE的长＝；

(2)、如图，过点E作EF∥CD交线段BD于点F，连接AF，求证：四边形ABEF是菱形；

(3)、如图，在（2）条件下，线段AE、BD相交于M，连接CE，求线段CE的长.

查看试题解析
25. 在平面直角坐标系xOy中，直线AB：y＝－x＋b分别与x、y轴交于A(3，0)、B两点.

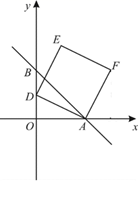(1)、如图，求点B的坐标；

(2)、点D为线段OB上的动点（点D不与点O重合），以AD为边，在第一象限内作正方形ADEF.
①如图，设点D为(0，m)，请用含m的代数式表示点F的坐标；

②如图，连结EB并延长交x轴于点G.当D点运动时，G点的位置是否发生变化？如果不变，请求出G点的坐标；如果变化，请说明理由.

查看试题解析