四川省简阳市镇金学区2019-2020学年七年级下学期数学期中考试试卷
试卷更新日期:2021-04-27 类型:期中考试
一、单选题
-
1. 如图,AD∥BC,点E在BD延长线上,若∠ADE=155°,则∠DBC的度数为( )
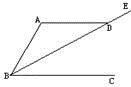 A、155° B、35° C、45° D、25°2. 可以写成( ).A、 B、 C、 D、3. 如图所示,已知直线AB,CD相较于O,OE平分∠COB,若∠EOB=55°,则∠BOD的度数是( )
A、155° B、35° C、45° D、25°2. 可以写成( ).A、 B、 C、 D、3. 如图所示,已知直线AB,CD相较于O,OE平分∠COB,若∠EOB=55°,则∠BOD的度数是( )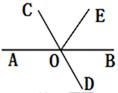 A、20 B、25° C、30° D、70°4. 在下列运算中,正确的是( )A、a2•a3=a5 B、(a2)3=a5 C、a6÷a2=a3 D、a5+a5=a105. 纳米是非常小的长度单位,1纳米=10-9米,目前发现一种新型病毒直径为25100纳米,用科学记数法表示该病毒直径是( )A、2.51×10-5米 B、25.1×10-6米 C、0.251×10-4米 D、2.51×10-4米6. 计算 的结果正确的是( )A、 B、 C、 D、7. 下列线段中能围成三角形的是( )A、1,2,3 B、4,5,6 C、5,6,11 D、7,10,188. 如图,BC⊥AE于点C,CD∥AB,∠B=55°,则∠1等于( )
A、20 B、25° C、30° D、70°4. 在下列运算中,正确的是( )A、a2•a3=a5 B、(a2)3=a5 C、a6÷a2=a3 D、a5+a5=a105. 纳米是非常小的长度单位,1纳米=10-9米,目前发现一种新型病毒直径为25100纳米,用科学记数法表示该病毒直径是( )A、2.51×10-5米 B、25.1×10-6米 C、0.251×10-4米 D、2.51×10-4米6. 计算 的结果正确的是( )A、 B、 C、 D、7. 下列线段中能围成三角形的是( )A、1,2,3 B、4,5,6 C、5,6,11 D、7,10,188. 如图,BC⊥AE于点C,CD∥AB,∠B=55°,则∠1等于( ) A、35° B、45° C、55° D、25°9. 如图,∠1的同旁内角共有( )
A、35° B、45° C、55° D、25°9. 如图,∠1的同旁内角共有( )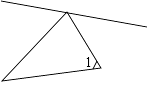 A、1个 B、2个 C、3个 D、4个10. 如图,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为( )
A、1个 B、2个 C、3个 D、4个10. 如图,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为( )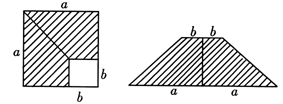 A、 B、 C、 D、无法确定
A、 B、 C、 D、无法确定二、填空题
-
11. 计算:-( )2=.12. 已知 ,则 的值是 .13. 已知实数a、b满足a-b=3,ab=2,则a²+b²的值为 。14. 已知a,b,c是△ABC的三边长,a,b满足|a﹣7|+(b﹣1)2=0,c为奇数,则c= .
15. 如图,在 中,点 是 上的点, ,将 沿着 翻折得到 ,则 °.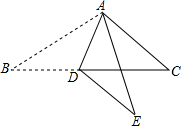 16. 若4x2+2(k-3)x+9是完全平方式,则k= .17. 若x﹣y=a , xy=a+3,且x2+y2=5,则a的值为 .18. 观察下面的解题过程,然后化简:
16. 若4x2+2(k-3)x+9是完全平方式,则k= .17. 若x﹣y=a , xy=a+3,且x2+y2=5,则a的值为 .18. 观察下面的解题过程,然后化简:(2+1)(22+1)(24+1)
=(2﹣1)(2+1)(22+1)(24+1)
=(22﹣1)(22+1)(24+1)
=(24﹣1)(24+1)
=28﹣1
化简:(3+1)(32+1)(34+1)(38+1)= .
19. 如图,直线AB∥CD∥EF,则∠α+∠β-∠γ=.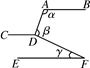 20. 如图,已知 ,添加下列条件中的一个:① ,② ,③ ,其中不能确定 ≌△ 的是(只填序号).
20. 如图,已知 ,添加下列条件中的一个:① ,② ,③ ,其中不能确定 ≌△ 的是(只填序号).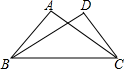
三、解答题
-
21. 计算:(1)、(2)、 ;(3)、 ;(4)、22. 已知-xm-2nym+n与-3x5y6的和是单项式,求 的值.23. 如图,已知AB∥CD, , 平分 , ,求 的度数.
 24. 如图:已知 ,猜想 与 的位置关系,并写出合适的理由.
24. 如图:已知 ,猜想 与 的位置关系,并写出合适的理由.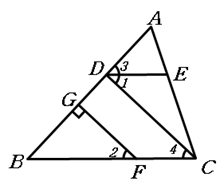 25. 如图,在△ABC中,AC=BC,∠C=90∘,AD是△ABC的角平分线,DE⊥AB,垂足为E.求证:AB=AC+CD.
25. 如图,在△ABC中,AC=BC,∠C=90∘,AD是△ABC的角平分线,DE⊥AB,垂足为E.求证:AB=AC+CD.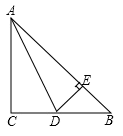 26. 利用我们学过的知识,可以得出下面这个优美的等式:
26. 利用我们学过的知识,可以得出下面这个优美的等式:;该等式从左到右的变形,不仅保持了结构的对称性,还体现了数学的和谐、简洁美.
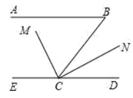
(1)、.请你证明这个等式;(2)、.如果 ,请你求出 的值.27. 如图,已知AM∥BN,∠A=60°,点P是射线M上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.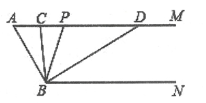 (1)、∠CBD=;(2)、当点P运动到某处时,∠ACB=∠ABD,则此时∠ABC=;(3)、在点P运动的过程中,∠APB与∠ADB的比值是否随之变化?若不变,请求出这个比值;若变化,请找出变化规律。28. 如图
(1)、∠CBD=;(2)、当点P运动到某处时,∠ACB=∠ABD,则此时∠ABC=;(3)、在点P运动的过程中,∠APB与∠ADB的比值是否随之变化?若不变,请求出这个比值;若变化,请找出变化规律。28. 如图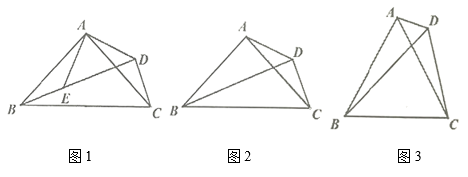 (1)、如图1,等腰 和等腰 中, , , , 三点在同一直线上,求证: ;(2)、如图2,等腰 中, , , 是三角形外一点,且 ,求证: ;(3)、如图3,等边 中, 是形外一点,且 ,
(1)、如图1,等腰 和等腰 中, , , , 三点在同一直线上,求证: ;(2)、如图2,等腰 中, , , 是三角形外一点,且 ,求证: ;(3)、如图3,等边 中, 是形外一点,且 ,① 的度数为;
② , , 之间的关系是.