四川省简阳市简阳市简城学区2019-2020学年七年级下学期数学期中考试试卷

试卷更新日期：2021-04-27 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各题中计算错误的是（）

A、［(-m³)²(-n²)³］³= -m¹⁸n¹⁸ B、(-m³n)²(-mn²)³= -m⁹n⁸ C、［(-m)²(-n²)³］³= - m⁶n⁶ D、(-m²n)³(-mn²)³= m⁹n⁹

查看试题解析
2. 化简x(y-x)-y(x-y)得（）

A、x²-y² B、y²-x² C、2xy D、-2xy

查看试题解析
3. 若 $2^{a} = 5$ ， $2^{b} = 3$ ，则 $2^{2 a - 3 b}$ 等于（）

A、 $\frac{27}{25}$ B、 $\frac{10}{9}$ C、 $\frac{3}{5}$ D、 $\frac{25}{27}$

查看试题解析
4. $x^{2} + 2 a x + 16$ 是一个完全平方式，则a的值为（）

A、4 B、8 C、4或-4 D、8或-8

查看试题解析
5. ${(\frac{3}{4})}^{- 2}$ 、 ${(\frac{6}{5})}^{2}$ 、 ${(\frac{7}{6})}^{0}$ 三个数中，最大的是（）

A、 ${(\frac{3}{4})}^{- 2}$ B、 ${(\frac{6}{5})}^{2}$ C、 ${(\frac{7}{6})}^{0}$ D、无法确定

查看试题解析
6. 如果两条平行线被第三条直线所截，那么一组同位角的平分线（）

A、互相平行 B、互相垂直 C、交角是锐角 D、交角是钝角

查看试题解析
7. 如图是赛车跑道的一段示意图，其中AB∥DE，测得∠B=140°，∠D=120°，则∠C度数为（）

A、120° B、100° C、140° D、90°

查看试题解析
8. 已知∠α和∠β互补，且∠α＞∠β，下列表示角的式子：①90°-∠β；②∠α-90°；③ $\frac{1}{2}$ （∠α+∠β）；④ $\frac{1}{2}$ （∠α-∠β）.其中能表示∠β的余角的有（）个.

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 已知△ABC的底边BC上的高为8 cm，当底边BC从16 cm变化到5 cm时，△ABC的面积（）

A、从20 cm²变化到64 cm² B、从40 cm²变化到128 cm² C、从128 cm²变化到40 cm² D、从64 cm²变化到20 cm²

查看试题解析
10. “龟兔赛跑”讲述了这样的故事：领先的兔子看着缓慢爬行的乌龟，骄傲起来，睡了一觉. 当它醒来时，发现乌龟快到终点了，于是急忙追赶，但为时已晚，乌龟还是先到达了终点……. 用 s₁、_s2 分别表示乌龟和兔子所行的路程， t 为时间，则下列图象中与故事情节相吻合的是（）

A、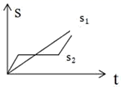 B、 C、 D、

查看试题解析

二、填空题

11. 已知：（x^3n-2）²x²ⁿ⁺⁴÷xⁿ=x^2n-5 ，则n=.

查看试题解析
12. 已知x＋y＝－5，xy＝6，则x²＋y²＝．

查看试题解析
13. 如图，若∠A=110°，AB∥CD，AD∥BC，则∠ECD=.

查看试题解析
14. 已知6^x=5，6^y=2，则6^{2x+ y}=.

查看试题解析
15. 已知长方形的面积是 $3 a^{2} - 3 b^{2}$ ，如果它的一边长是 $a + b$ ，则它的周长是.

查看试题解析
16. 已知一个角的余角是这个角的补角的 $\frac{1}{4}$ ，求这个角的度数为.

查看试题解析
17. 一根弹簧原长13厘米，挂物体质量不得超过16千克，并且每挂1千克就伸长0.5厘米，则当挂物体质量为10千克，弹簧长度为厘米，挂物体质量x(千克)与弹簧长度y(厘米)的关系式为

查看试题解析
18. 已知 $a - b = b - c = \frac{3}{5}$ ， $a^{2} + b^{2} + c^{2} = 1$ ，则 $a b + b c + a c$ 的值等于.

查看试题解析
19. 已知a₁= $1 - \frac{1}{2^{2}}$ ，a₂= $1 - \frac{1}{3^{2}}$ ，a₃= $1 - \frac{1}{4^{2}}$ ，…，a_n= $1 - \frac{1}{{(n + 1)}^{2}}$ ，S_n=a₁•a₂…a_n ，则S₂₀₁₅=.

查看试题解析

三、解答题

20.

(1)、计算：[（4b+3a）（3a﹣4b）﹣（b﹣3a）²]÷4b

(2)、先化简，再求值.（2x﹣1）（2x+1）﹣（x﹣2）²﹣（x+2）² ，其中 $x = - 3 \frac{1}{3}$ .

查看试题解析
21. 如图所示，一个四边形纸片ABCD，∠B=∠D=90°，把纸片按如图所示的方式折叠，使点B落在AD边上的B′点，AE是折痕.

(1)、试判断B′E与DC的位置关系；

(2)、如果∠C=130°，求∠AEB的度数.

查看试题解析
22. 有一边长为xcm的正方形，若边长变化，则其面积也随之变化.

(1)、在这个变化过程中，自变量和因变量各是什么？

(2)、写出正方形的面积y(cm²)关于正方形的边长x(cm)的关系式.

查看试题解析
23. 某生物兴趣小组在四天的试验研究中发现：骆驼的体温会随外部环境温度的变化而变化，而且在这四天中每昼夜的体温变化情况相同.他们将一头骆驼前两昼夜的体温变化情况绘制成如图所示的图象，请根据图象完成下列问题：

(1)、第一天中，在什么时间范围内这头骆驼的体温是上升的？它的体温从最低上升到最高需要多长时间？

(2)、第三天12时这头骆驼的体温是多少？

查看试题解析
24.

(1)、若a+b=3，ab=2，求a⁴+b⁴的值.

(2)、已知aⁿ=2，求(2a³ⁿ)²-3(a²)²ⁿ÷a²ⁿ的值.

查看试题解析
25. 已知：如图，AE⊥BC，FG⊥BC，∠1＝∠2，∠D＝∠3+60°，∠CBD＝70°.

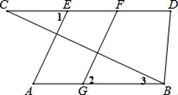(1)、求证：AB∥CD；

(2)、求∠C的度数.

查看试题解析
26. 某机动车出发前油箱内有油42L，行驶若干小时后，途中在加油站加油若干升．油箱中余油量Q（L）与行驶时间t（h）之间的函数关系如图所示，根据图回答问题：

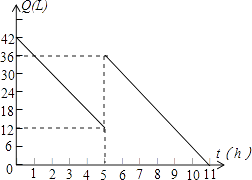(1)、机动车行驶5h后加油，途中加油升；

(2)、根据图形计算，机动车在加油前的行驶中每小时耗油多少升？

(3)、如果加油站距目的地还有400km，车速为60km/h，要到达目的地，油箱中的油是否够用？请说明理由．

查看试题解析
27. 你能求（x一1）（x⁹⁹+x⁹⁸+x⁹⁷+…+x+1）的值吗?
遇到这样的问题，我们可以先思考一下，从简单的情形人手，分别计算下列各式的值.

(1)、（x－1）（x+1） =；

(2)、（x—1）（ x²+x+1） =；

(3)、（x－1）（x³+ x²+x+1） =；
…

由此我们可以得到：

(4)、（x一1）（ x⁹⁹+x⁹⁸+x⁹⁷+…+x+1） = ，
请你利用上面的结论，完成下列的计算：

(5)、2⁹⁹+2⁹⁸+2⁹⁷+…+2+1；

查看试题解析
28. 若（x²+3mx﹣ $\frac{1}{3}$ ）（x²﹣3x+n）的积中不含x和x³项，

(1)、求m²﹣mn+ $\frac{1}{4}$ n²的值；

(2)、求代数式（﹣18m²n）²+（9mn）^﹣²+（3m）²⁰¹⁴n²⁰¹⁶的值.

查看试题解析