四川省成都市龙泉驿区2019-2020学年七年级下学期数学期中考试试卷
试卷更新日期：2021-04-27 类型：期中考试
一、单选题
-
1. 计算（﹣a）5÷a3结果正确的是（ ）A、a2 B、﹣a2 C、﹣a3 D、﹣a42. 整式x2+kx+16为某完全平方式展开后的结果，则k的值为（ ）A、4 B、﹣4 C、±4 D、±83.
如图，已知直线a、b被直线c所截，那么∠1的同位角是（ ）
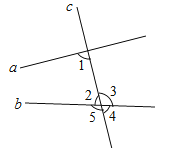A、∠2 B、∠3 C、∠4 D、∠54. 在利用太阳能热水器来加热水的过程中，热水器里的水温随所晒时间的长短而变化，这个问题中因变量是（ ）A、太阳光强弱 B、水的温度 C、所晒时间 D、热水器的容积5. 下列事件中，是必然事件的是（ ）A、足球运动员射门一次，球射进球门 B、随意翻开一本书，这页的页码是奇数 C、经过有交通信号灯的路口，遇到绿灯 D、任意画一个三角形，其内角和是180°6. 冠状病毒有多种类型，新型冠状病毒也是其中的一种.冠状病毒的直径在60﹣220纳米之间，平均直径为100纳米左右（1纳米＝10﹣9米）.那么100纳米可用科学记数法表示为（ ）A、100×10﹣9米 B、100×109米 C、1×10﹣7米 D、1×107米7. 计算（x3y）3÷（2xy）3的结果应该是（ ）A、 B、 C、 D、8. 如图，直线AB∥CD，将含有45°角的三角板EFP的直角顶点F放在直线CD上，顶点E放在直线AB上，若∠1=30°，则∠2的度数为（ ）
A、15° B、17° C、20° D、30°9. 用直尺和圆规作∠HDG＝∠AOB的过程中，弧②是（ ）
A、以D为圆心，以DN为半径画弧 B、以M为圆心，以DN长为半径画弧 C、以M为圆心，以EF为半径画弧 D、以D为圆心，以EF长为半径画弧10. “龟兔赛跑”讲述了这样的故事：领先的兔子看着缓慢爬行的乌龟，骄傲起来，睡了 一觉. 当它醒来时，发现乌龟快到终点了，于是急忙追赶，但为时已晚，乌龟还是先到达了终 点……. 用 s1 、s2 分别表示乌龟和兔子所行的路程， t 为时间，则下列图象中与故事情节相吻合的是（ ）A、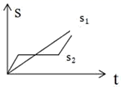
B、
C、
D、
二、填空题
-
11. 计算：（a+1）（a﹣1）=.12. 按程序x⇒平方⇒+x⇒÷x⇒﹣3x进行运算后，结果用x的代数式表示是.（填入运算结果的最简形式）13. 一个袋子中有红球和白球两种，从中摸出红球的概率为 .已知袋子中红球有10个，则袋子中白球的个数为.14. 如图：已知AB∥CD，CE∥BF，∠AEC＝45°，则∠BFD＝.
15. 如图是一个可以自由转动的转盘，转盘分成6个大小相同的扇形，颜色分为红、绿、黄三种颜色.指针的位置固定，转动的转盘停止后，其中的某个扇形会恰好停在指针所指的位置（指针指向两个扇形的交线时，当作指向右边的扇形）.转动一次转盘后，指针指向颜色的可能性大.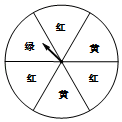
16. 如图，直线AB∥CD，OA⊥OB，若∠1=140°，则∠2=度.
17. x2+ x+＝（）+）2.18. 已知（5+2x）2+（3﹣2x）2＝40，则（5+2x）•（3﹣2x）的值为.19. 如图①：MA1∥NA2 ， 图②：MA1∥NA3 ， 图③：MA1∥NA4 ， 图④：MA1∥NA5 ， ……，
则第8个图中的∠A1+∠A2+∠A3+…+∠A8＝.
三、解答题
-
20. 计算(1)、2018×2020﹣20192；(2)、3x5•x2﹣5（x3）3÷x2.21. 化简求值(1)、（2x+1）2﹣4（x﹣1）（x+1），其中x＝ ；(2)、[（x+2y）2﹣（x+y）（3x﹣y）﹣5y2]÷（2x），其中x＝﹣2，y＝ .22. 已知：如图，AB∥CD，EF分别交AB、CD于点E、F，EG平分∠AEF，FH平分∠EFD，求证：EG∥FH.
证明：∵AB∥CD（ ），
∴∠AEF＝∠EFD（ ），
∵EG平分∠AEF，FH平分∠EFD（ ），
∴∠▲ ＝ ∠AEF，
∠ ▲ ＝ ∠EFD（角平分线定义），
∴∠▲ ＝∠▲ .
∴EG∥FH（ ）
23.如图表示的是汽车在行驶的过程中，速度随时间变化而变化的情况．
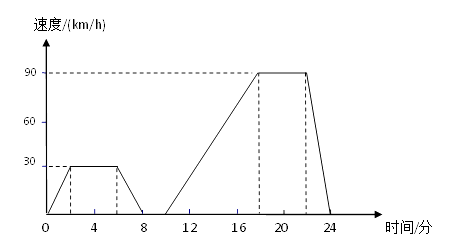(1)、汽车从出发到最后停止共经过了多少时间？它的最高时速是多少？(2)、汽车在那些时间段保持匀速行驶？时速分别是多少？(3)、出发后8分到10分之间可能发生了什么情况？(4)、用自己的语言大致描述这辆汽车的行驶情况．24. 若a+b＝3，ab＝1.求
(1)、a2+b2；(2)、（a﹣b）2；(3)、ab3+a3b.25. 如图，已知AB∥CD，∠A＝∠D，求证：∠CGE＝∠BHF.
26.(1)、已知am＝2，an＝3.求am+n的值；(2)、已知n为正整数，且x2n＝7.求7（x3n）2﹣3（x2）2n的值.27. 已知（x+1）5＝ax5+bx4+cx3+dx2+ex+f.当x＝1时，（1+1）5＝a×15+b×14+c×13+d×12+e×1+f
＝a+b+c+d+e+f
∴a+b+c+d+e+f＝25＝32
这种给x取一个特殊数的方法叫赋值法.请你巧用赋值法，尝试解答下列问题.
(1)、求当x为多少时，可求出f，f为多少？(2)、求﹣a+b﹣c+d﹣e+f的值；(3)、求b+d+f的值.28. 已知AM∥CN，点B为平面内一点，AB⊥BC于B.
(1)、如图1，直接写出∠A和∠C之间的数量关系；(2)、如图2，过点B作BD⊥AM于点D，∠BAD与∠C有何数量关系，并说明理由；(3)、如图3，在（2）问的条件下，点E，F在DM上，连接BE，BF，CF，BF平分∠DBC，BE平分∠ABD，若∠FCB+∠NCF=180°，∠BFC=5∠DBE，求∠EBC的度数.