福建省南平市2019-2020学年七年级下学期数学期中考试试卷
试卷更新日期:2021-04-27 类型:期中考试
一、单选题
-
1. 9的平方根是( )A、3 B、±3 C、 D、±2. 下列实数是无理数的是( )A、1.732 B、 C、 D、03. 在平面直角坐标系中,点P(2,﹣3)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 下列方程组是二元一次方程组的是( )A、 B、 C、 D、5. 如图,点 在 的延长线上,下列条件不能判定 的是( )
 A、 B、 C、 D、6. 在平面直角坐标系中,若 轴上的点 到 轴的距离为2,则点 的坐标为( )A、 B、 或 C、 D、 或7. 象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“炮”和“馬”的点的坐标分别为 ,则表示棋子“帥”的点的坐标为( )
A、 B、 C、 D、6. 在平面直角坐标系中,若 轴上的点 到 轴的距离为2,则点 的坐标为( )A、 B、 或 C、 D、 或7. 象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“炮”和“馬”的点的坐标分别为 ,则表示棋子“帥”的点的坐标为( ) A、 B、 C、 D、8. 在下列各组 的值中,不是方程 的解的是( )A、 B、 C、 D、9. 已知关于 的二元一次方程组 的解也是方程 的解,那么 的值为( )A、3 B、4 C、-3 D、-410. 如图,点 为定点,直线 是直线 上一动点.对于下列各值:①线段 的长;② 的度数;③ 的周长;④ 的面积.其中不会随点 的移动而变化的是( )
A、 B、 C、 D、8. 在下列各组 的值中,不是方程 的解的是( )A、 B、 C、 D、9. 已知关于 的二元一次方程组 的解也是方程 的解,那么 的值为( )A、3 B、4 C、-3 D、-410. 如图,点 为定点,直线 是直线 上一动点.对于下列各值:①线段 的长;② 的度数;③ 的周长;④ 的面积.其中不会随点 的移动而变化的是( ) A、①③ B、①④ C、②③ D、②④
A、①③ B、①④ C、②③ D、②④二、填空题
-
11. 如图,∵ 为垂足,∴ 和 重合,理由是.
 12. 已知 是正整数,则正整数 的最小值是.13. 已知平面内一点 ,若 满足条件 ,则点 的位置是.14. 《孙子算经》中有一道题:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”译文大致是:“用一根绳子去量一根木条,绳子剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?”如果设木条长x尺,绳子长y尺,可列方程组为;15. 如图①是长方形纸带,将纸带沿EF折叠成图②,再沿BF折叠成图③,若∠DEF=x,将图③中∠CFE用x表示为
12. 已知 是正整数,则正整数 的最小值是.13. 已知平面内一点 ,若 满足条件 ,则点 的位置是.14. 《孙子算经》中有一道题:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”译文大致是:“用一根绳子去量一根木条,绳子剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?”如果设木条长x尺,绳子长y尺,可列方程组为;15. 如图①是长方形纸带,将纸带沿EF折叠成图②,再沿BF折叠成图③,若∠DEF=x,将图③中∠CFE用x表示为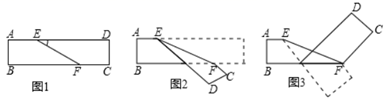
三、解答题
-
16.(1)、计算: .(2)、求 中 的值.17. 由于受到新冠病毒疫情的影响,某医药厂根据市场调查得知某种消毒液的大瓶装(500克)和小瓶装(250克)两种产品的销售数量比为 (按瓶计算),若该厂每天生产这种消毒液22.5吨,为了满足市场需求,求这种消毒液应该分装大、小瓶两种产品各多少瓶.18. 完成下面的证明:已知:如图, 平分 平分 ,且
求证: .
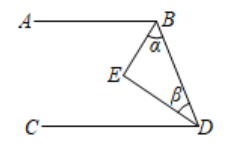
证明: 平分 平分 (已知),
▲ ,
▲ , ( ▲ )
( ▲ )
(已知)
▲ , ( ▲ )
( ▲ )
19. 如图,在平面直角坐标系中,已知点 是△ 的边 上任意一点,△ 经过平移后得到△ 点 的对应点为 . (1)、直接写出点 的坐标.(2)、在图中画出△ .(3)、求△ 的面积.20. 已知关于 的二元一次方程组 ,甲同学正确解得 ,而乙同学粗心,把 看错了,解得 ,求 的值.21. 已知:如图,在△ABC中,过点A作AD⊥BC,垂足为D,E为AB上一点,过点E作EF⊥BC,垂足为F,过点D作DG∥AB交AC于点G.
(1)、直接写出点 的坐标.(2)、在图中画出△ .(3)、求△ 的面积.20. 已知关于 的二元一次方程组 ,甲同学正确解得 ,而乙同学粗心,把 看错了,解得 ,求 的值.21. 已知:如图,在△ABC中,过点A作AD⊥BC,垂足为D,E为AB上一点,过点E作EF⊥BC,垂足为F,过点D作DG∥AB交AC于点G. (1)、依题意补全图形;(2)、请你判断∠BEF与∠ADG的数量关系,并加以证明.22.(1)、采用夹逼法,利用 的一系列不足近似值和过剩近似值来估计它的大小的过程如下:
(1)、依题意补全图形;(2)、请你判断∠BEF与∠ADG的数量关系,并加以证明.22.(1)、采用夹逼法,利用 的一系列不足近似值和过剩近似值来估计它的大小的过程如下:∵ ,
∴
∵ , ,
∴
∵ ,
∴
∵ ,
∴
因此 (精确到百分位),
使用夹逼法,求出 的近似值(精确到百分位).
(2)、我们规定用符号 表示数 的整数部分,例如①按此规定 ;
②如果 的整数部分是 的小数部分是 求 的值.
23. 在平面直角坐标系xOy中,对于任意三点A,B,C的“矩面积”,给出如下定义:“水平底”a:任意两点横坐标差的最大值,“铅垂高”h:任意两点纵坐标差的最大值,则“矩面积”S=ah.例如:三点坐标分别为A(1,2),B(-3,1),C(2,-2),则“水平底”a=5,“铅垂高”h=4,“矩面积”S=ah=20.根据所给定义解决下列问题:(1)、若已知点D(1,2)、E(-2,1)、F(0,6),则这3点的“矩面积”=.(2)、若D(1,2)、E(-2,1)、F(0,t)三点的“矩面积”为18,求点F的坐标;24. 探究题:学完平行线的性质与判定之后,我们发现借助构造平行线的方法可以帮我们解决许多问题.(1)、小明遇到了下面的问题:如图1, ,点 在 内部,探究 之间的关系.小明过点 作 的平行线,可证得 之间的数量关系是: .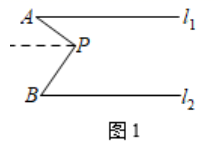 (2)、如图2,若 ,点 在 的外部, 之间的数量关系是否会发生变化?请证明你的结论.
(2)、如图2,若 ,点 在 的外部, 之间的数量关系是否会发生变化?请证明你的结论.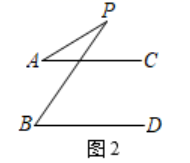 (3)、试构造平行线解决以下问题:如图3,一条河流的两岸 当小船行驶到河中 点时,与两岸码头 所形成的夹角为 即 ),当小船行驶到河中点 时,恰好满足 请你求出此时点 与码头 所形成的夹角 的度数.
(3)、试构造平行线解决以下问题:如图3,一条河流的两岸 当小船行驶到河中 点时,与两岸码头 所形成的夹角为 即 ),当小船行驶到河中点 时,恰好满足 请你求出此时点 与码头 所形成的夹角 的度数.