福建省闽侯县2019-2020学年七年级下学期数学期中考试试卷

试卷更新日期：2021-04-27 类型：期中考试

进入出卷网下载

一、单选题

1. 9的平方根是（）

A、 9 B、3 C、±9 D、±3

查看试题解析
2. 如图，∠1，∠2是对顶角的是（）

A、 B、 C、 D、

查看试题解析
3. 在实数 $\sqrt{5}$ ， $\frac{5}{6}$ ， $\sqrt[3]{- 8}$ ，3.14， $\frac{π}{3}$ ， $\sqrt{36}$ ， $0.1010010001$ 中，无理数有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
4. 将一直角三角板与两边平行的纸条如图放置若∠1=60°，则∠2的度数为（）

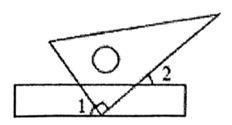A、60° B、45° C、50° D、30°

查看试题解析
5. 如图，数轴上表示实数 $\sqrt{5}$ 的点可能是（）

A、点 $A$ B、点 $B$ C、点 $C$ D、点 $D$

查看试题解析
6. 下列命题是真命题的是（）

A、相等的角是对顶角 B、在同一平面内，如果 $a ⊥ b$ ， $b ⊥ c$ ，则 $a ⊥ c$ C、内错角相等 D、如果 $a // b$ ， $b // c$ ，则 $a // c$

查看试题解析
7. 如图所示，下列推理不正确的是（）

A、若 $∠ 1 = ∠ B$ ，则 $B C // D E$ B、若 $∠ 2 = ∠ A D E$ ，则 $A D // C E$ C、若 $∠ A + ∠ A D C = 180 °$ ，则 $A B // C D$ D、若 $∠ B + ∠ B C D = 180 °$ ，则 $B C // D E$

查看试题解析
8. 如果方程 $x - y = 3$ 与下面方程中的一个组成的方程组的解为 ${\begin{array}{l} x = 4, \\ y = 1, \end{array}$ 那么这个方程可以

A、 $\frac{x}{4} + 2 y = 5$ B、 $3 x - 4 y = 16$ C、 $\frac{x}{2} + 3 y = 8$ D、 $2 (x - y) = 6 y$

查看试题解析
9. 某运输队接到给武汉运输物资的任务，该队有 $A$ 型卡车和 $B$ 型卡车， $A$ 型卡车每次可运输 $6 t$ 物资，每天可来回6次， $B$ 型卡车每次可运输 $10 t$ 物资，每天可来回4次，若每天派出20辆卡车，刚好运输 $860 t$ 物资，设该运输队每天派出 $A$ 型卡车 $x$ 辆， $B$ 型卡车 $y$ 辆，则所列方程组正确的是（）

A、 ${\begin{array}{l} 6 x + 4 y = 20 \\ 6 x + 10 y = 860 \end{array}$ B、 ${\begin{array}{l} x + y = 20 \\ 6 \cdot 6 x + 4 \cdot 10 y = 860 \end{array}$ C、 ${\begin{array}{l} x + y = 20 \\ 6 x + 10 y = 860 \end{array}$ D、 ${\begin{array}{l} 6 x + 4 y = 20 \\ 6 \cdot 6 x + 4 \cdot 10 y = 860 \end{array}$

查看试题解析
10. 若有 $\sqrt[3]{x} + \sqrt[3]{y} = 0$ ，则 $x$ 和 $y$ 的关系是（）

A、 $x = y = 0$ B、 $x - y = 0$ C、 $x y = 1$ D、 $x + y = 0$

查看试题解析

二、填空题

11. 计算： $\sqrt{64} =$ ； $\sqrt[3]{- \frac{1}{8}} =$ .

查看试题解析
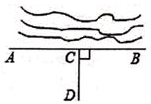
12. 已知 $x = 1$ ， $y = - 8$ 是方程 $3 a x - y = - 1$ 的解，则a的值为．

查看试题解析
13. 如图，要把池中的水引到D处，可过D点作CD⊥AB于C，然后沿CD开渠，可使所开渠道最短，试说明设计的依据：。

查看试题解析
14. 把命题改写成“如果……，那么……”的形式：两直线平行，同位角相等..

查看试题解析
15. 已知 $∠ α$ 与 $∠ β$ 互补，且 $∠ α$ 与 $∠ β$ 的差是70°，则 $∠ α =$ ， $∠ β =$ .

查看试题解析
16. 一束光线照射到平面镜 $A B$ 上，然后在平面镜 $A B$ 和 $C D$ 之间来回反射，这时光线的入射角等于反射角，即 $∠ 1 = ∠ 2$ ， $∠ 3 = ∠ 4$ ， $∠ 5 = ∠ 6$ .若已知 $∠ 1 = 50 °$ ， $∠ 6 = 65 °$ ，那么∠3的度数为.

查看试题解析

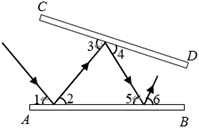
三、解答题

17. 计算：

(1)、 $| \sqrt{5} - \sqrt{7} | + \sqrt{5}$ ；

(2)、 $\sqrt{0.09} + \sqrt[3]{- 8} - \sqrt{\frac{1}{4}}$

查看试题解析
18. 解下列方程组： ${\begin{array}{l} 2 x + 3 y = 4 \\ 3 x - 2 y = - 7 \end{array}$

查看试题解析
19. 某小组去看电影，甲种票每张24元，乙种票每张20元.如果40人购票恰好用去920元，甲乙两种票各买了多少张？

查看试题解析
20. 完成下列证明：
已知 $C D ⊥ A B$ ， $F G ⊥ A B$ ，垂足分别为 $D$ 、 $F$ ，且 $∠ 1 = ∠ 2$ ，求证 $D E // B C$ .

证明：∵ $A B ⊥ C D$ ， $F G ⊥ A B$ （已知），

∴ $∠ B D C = ∠ B F G = 90 °$ （_▲_）

∴ $C D // G F$ （_▲_）

∴ $∠ 2 = ∠ 3$ （_▲_）

又∵ $∠ 1 = ∠ 2$ （已知）

∴ $∠ 1 = ∠ 3$ （等量代换）

∴ $D E // B C$ （_▲_）

查看试题解析
21. 已知 $4 a + 7$ 的立方根是3， $2 a + 2 b + 2$ 的算术平方根是4.

(1)、求 $a$ ， $b$ 的值；

(2)、求 $6 a + 3 b$ 的平方根.

查看试题解析
22. 如图，已知 $A C ⊥ B C$ 于点 $C$ ， $∠ D A B = 70 °$ ， $A C$ 平分 $∠ D A B$ ， $∠ D C A = 35 °$ .求 $∠ B$ 的度数.

查看试题解析

23. 某电器超市销售每台进价分别为2000元、1700元的

A

、

B

两种型号的空调，如表是近两周的销售情况：

销售时段	销售数量		销售款
销售时段	$A$ 种型号	$B$ 种型号	销售款
第一周	4台	5台	20500元
第二周	5台	10台	33500元

(1)、求

A

、

B

两种型号的空调的销售单价；

(2)、求近两周的销售利润.

查看试题解析

24. 先阅读下面材料，再解答问题：
材料：已知 $a$ ， $b$ 是有理数，并且满足等式 $5 - \sqrt{7} a = 2 b + \frac{2}{3} \sqrt{7} - a$ ，求 $a$ ， $b$ 的值.

解：∵ $5 - \sqrt{7} a = 2 b + \frac{2}{3} \sqrt{7} - a$

∴ $5 - \sqrt{7} a = (2 b - a) + \frac{2}{3} \sqrt{7}$

∵ $a$ ， $b$ 是有理数

∴ ${\begin{array}{l} 2 b - a = 5 \\ - a = \frac{2}{3} \end{array}$ 解得 ${\begin{array}{l} a = - \frac{2}{3} \\ b = \frac{13}{6} \end{array}$

问题：

(1)、已知 $a$ ， $b$ 是有理数， $a + 3 \sqrt{2} = 5 + \sqrt{2} b$ ，则 $a =$ ， $b =$ .

(2)、已知 $x$ ， $y$ 是有理数，并且满足等式 $7 x - 9 + \sqrt{2} x = - 5 y + \sqrt{2} y + 3 \sqrt{2}$ ，求 $x$ ， $y$ 的值.

查看试题解析
25. 如图1， $A M // C N$ ，点 $B$ 为平面内一点， $A B ⊥ B C$ 于 $B$ ，过 $B$ 作 $B D ⊥ C N$ ，垂足为 $D$ .

(1)、求证： $∠ B A M = ∠ C B D$ ；

(2)、如图2，分别作 $∠ C B D$ 、 $∠ A B D$ 的平分线交 $D N$ 于 $E$ 、 $F$ ，连接 $A F$ ，若 $∠ C B F = \frac{5}{4} ∠ C B E$ ，

①求 $∠ C B E$ 的度数；

②求证： $∠ C B F = ∠ C F B$ .

查看试题解析