河南省名校2021年数学中考一模试卷
试卷更新日期:2021-04-27 类型:中考模拟
一、单选题
-
1. 下列各数中,绝对值最小的数是( )A、 B、 C、 D、2. 将867000用科学记数法表示为( )A、 B、 C、 D、3. 为调动学生参与体育锻炼的积极性,某校组织了一分钟跳绳比赛活动,体育组随机抽取了10名参赛学生的成绩,将这组数据整理后制成统计表:
一分钟跳绳个数(个)
141
144
145
146
学生人数(名)
5
2
1
2
则关于这组数据的结论正确的是( )
A、平均数是144 B、众数是141 C、中位数是144.5 D、方差是5.44. 函数 与 的图象如图所示,则 的大致图象为( )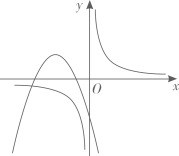 A、
A、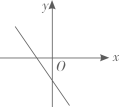 B、
B、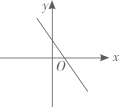 C、
C、 D、
D、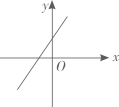 5. 下列几何体是由4个相同的小正方体搭成的,其中,主视图、左视图、俯视图都相同的是( )A、
5. 下列几何体是由4个相同的小正方体搭成的,其中,主视图、左视图、俯视图都相同的是( )A、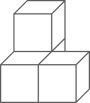 B、
B、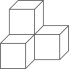 C、
C、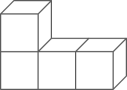 D、
D、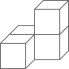 6. 如图,三角板的直角顶点落在矩形纸片的一边上.若∠1=35°,则∠2的度数是( )
6. 如图,三角板的直角顶点落在矩形纸片的一边上.若∠1=35°,则∠2的度数是( ) A、35° B、45° C、55° D、65°7. 方程2x2﹣8x﹣1=0的解的情况是( )A、有两个不相等的实数根 B、没有实数根 C、有两个相等的实数根 D、有一个实数根8. 近年来,“快递业”成为我国经济的一匹“黑马”,2017年我国快递业务量为400亿件,2019年快递量将达到600亿件,设快递量平均每年增长率为x,则下列方程中正确的是( )A、400(1+x)=600 B、400(1+2x)=600 C、400(1+x)2=600 D、600(1﹣x)2=4009. 如图,在矩形ABCD中,AB=3,BC=4,动点P沿折线BCD从点B开始运动到点D,设点P运动的路程为x,△ADP的面积为y,那么y与x之间的函数关系的图象大致是( )
A、35° B、45° C、55° D、65°7. 方程2x2﹣8x﹣1=0的解的情况是( )A、有两个不相等的实数根 B、没有实数根 C、有两个相等的实数根 D、有一个实数根8. 近年来,“快递业”成为我国经济的一匹“黑马”,2017年我国快递业务量为400亿件,2019年快递量将达到600亿件,设快递量平均每年增长率为x,则下列方程中正确的是( )A、400(1+x)=600 B、400(1+2x)=600 C、400(1+x)2=600 D、600(1﹣x)2=4009. 如图,在矩形ABCD中,AB=3,BC=4,动点P沿折线BCD从点B开始运动到点D,设点P运动的路程为x,△ADP的面积为y,那么y与x之间的函数关系的图象大致是( )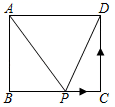 A、
A、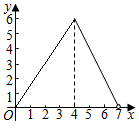 B、
B、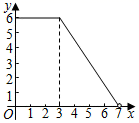 C、
C、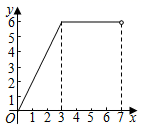 D、
D、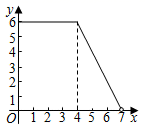 10. 如图,在菱形ABCD中,按以下步骤作图:①分别以点C和点D为圆心,大于 为半径作弧,两弧交于点M,N;②作直线MN,且 恰好经过点A,与CD交于点E,连接BE,则下列说法错误的是( )
10. 如图,在菱形ABCD中,按以下步骤作图:①分别以点C和点D为圆心,大于 为半径作弧,两弧交于点M,N;②作直线MN,且 恰好经过点A,与CD交于点E,连接BE,则下列说法错误的是( )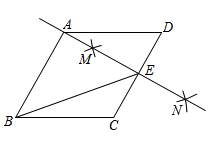 A、 B、 C、若AB=4,则 D、
A、 B、 C、若AB=4,则 D、二、填空题
-
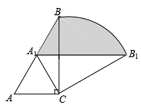
11. 计算: .12. 若关于x的不等式组 有且只有三个整数解,则m的取值范围是 .13. 从甲、乙、丙、丁4名三好学生中随机抽取2名学生担任国旗队升旗手,则抽取的2名学生恰好是乙和丙的概率是 .14. 如图,Rt△ABC 中,∠ACB=90°,∠ABC=30°,AC=2,将△ABC绕点C顺时针旋转,点A、B的对应点分别为A1、B1 , 当点A1恰好落在AB上时,弧BB1与点A1构成的阴影部分的面积为.
 15. 正方形 的边长为4,点 在对角线 上(可与点 重合), ,点 在正方形的边上.下面四个结论中,
15. 正方形 的边长为4,点 在对角线 上(可与点 重合), ,点 在正方形的边上.下面四个结论中,①存在无数个四边形 是平行四边形;
②存在无数个四边形 是菱形;
③存在无数个四边形 是矩形;
④至少存在一个四边形 是正方形.
所有正确结论的序号是 .
三、解答题
-
16.(1)、计算:(2)、下面是小彬同学进行分式化简的过程,请认真阅读并完成相应任务.
第一步
第二步
第三步
第四步
第五步
第六步
任务一:填空:①以上化简步骤中,第_▲_步是进行分式的通分,通分的依据是__▲__或填为__▲ ;
②第_▲__步开始出现错误,这一步错误的原因是__▲__;
任务二:请直接写出该分式化简后的正确结果;
任务三:除纠正上述错误外,请你根据平时的学习经验,就分式化简时还需要注意的事项给其他同学提一条建议.
17. 为了解某校八年级学生一门课程的学习情况,小佳和小丽分别对八年级1班和2班本门课程的期末成绩进行了调查分析.小佳对八年级1班全班学生(25名)的成绩进行分析,过程如下收集、整理数据:表一:
分数段
班级
八年级1班
7
5
10
3
表二:
统计量
班级
平均数
中位数
众数
极差
方差
八年级1班
78
85
36
105.28
小丽用同样的方式对八年级2班全班学生(25名)的成绩进行分析,变数据如下:
统计量
班级
平均数
中位数
众数
极差
方差
八年级2班
75
76
73
44
146.8
根据以上信息,解决下列问题:
(1)、已知八年级1班学生的成绩处在 这一组的数据如下: .根据上述数据,将表二补充完整:(2)、你认为哪个班级的成绩更为优异?请说明理由18. 如图,某人在山坡坡脚 处测得一座建筑物顶点 的仰角为 ,沿山坡向上走到 处再测得该建筑物顶点 的仰角为 .已知 米, , 的延长线交于点 ,山坡坡度为 (即 ).注:取 为 .
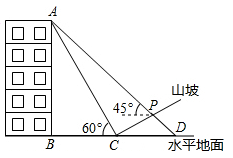 (1)、求该建筑物的高度(即 的长).(2)、求此人所在位置点 的铅直高度(测倾器的高度忽略不计).(3)、若某一时刻, 米长木棒竖放时,在太阳光线下的水平影长是 米,则同一时刻该座建筑物顶点 投影与山坡上点 重合,求点 到该座建筑物的水平距离.19. 下面是小石设计的“过圆上一点作圆的切线”的尺规作图的过程.
(1)、求该建筑物的高度(即 的长).(2)、求此人所在位置点 的铅直高度(测倾器的高度忽略不计).(3)、若某一时刻, 米长木棒竖放时,在太阳光线下的水平影长是 米,则同一时刻该座建筑物顶点 投影与山坡上点 重合,求点 到该座建筑物的水平距离.19. 下面是小石设计的“过圆上一点作圆的切线”的尺规作图的过程.
已知:如图1, 及 上一点P.
求作:直线PQ,使得PQ与 相切.
作法:如图2,
①连接PO并延长交 于点A;
②在 上任取一点B(点P,A除外),以点B为圆心,BP长为半径作 ,与射线PO的另一个交点为C.
③连接CB并延长交 于点Q.
④作直线PQ;
所以直线PQ就是所求作的直线.
根据小石设计的尺规作图的过程.
(1)、使用直尺和圆规,补全图形:(保留作图痕迹)(2)、完成下面的证明.证明:∵CQ是的 直径,
∴ __▲__ (__▲__)(填推理的依据)
∴ .
又∵OP是 的半径,
∴PQ是 的切线(_▲_)(填推理的依据)
20. 在△ABC中.BC边的长为x,BC边上的高为y,△ABC的面积为2.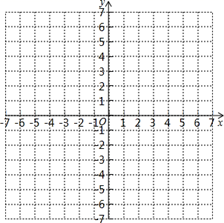 (1)、y关于x的函数关系式是 , x的取值范围是;(2)、在平面直角坐标系中画出该函数图象;(3)、将直线y=-x+3向上平移a(a>0)个单位长度后与上述函数图象有且只有一个交点,请求出此时a的值.21. 在近期“抗疫”期间,某药店销售A、B两种型号的口罩,已知销售800只A型和450只B型的利润为210元,销售400只A型和600只B型的利润为180元.(1)、求每只A型口罩和B型口罩的销售利润;(2)、该药店计划一次购进两种型号的口罩共2000只,其中B型口罩的进货量不超过A型口罩的3倍,设购进A型口罩x只,这2000只口罩的销售总利润为y元.
(1)、y关于x的函数关系式是 , x的取值范围是;(2)、在平面直角坐标系中画出该函数图象;(3)、将直线y=-x+3向上平移a(a>0)个单位长度后与上述函数图象有且只有一个交点,请求出此时a的值.21. 在近期“抗疫”期间,某药店销售A、B两种型号的口罩,已知销售800只A型和450只B型的利润为210元,销售400只A型和600只B型的利润为180元.(1)、求每只A型口罩和B型口罩的销售利润;(2)、该药店计划一次购进两种型号的口罩共2000只,其中B型口罩的进货量不超过A型口罩的3倍,设购进A型口罩x只,这2000只口罩的销售总利润为y元.①求y关于x的函数关系式;
②该药店购进A型、B型口罩各多少只,才能使销售总利润最大?
(3)、在销售时,该药店开始时将B型口罩提价100%,当收回成本后,为了让利给消费者,决定把B型口罩的售价调整为进价的15%,求B型口罩降价的幅度.22. 在平面直角坐标系 中,关于x的二次函数 的图象过点 , .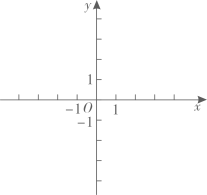 (1)、求这个二次函数的表达式;(2)、求当 时,y的最大值与最小值的差;(3)、一次函数 的图象与二次函数 的图象交点的横坐标分别是a和b,且 ,求m的取值范围.23. 在 中, , ,点P是平面内不与点A,C重合的任意一点,连接CP,将线段CP绕点P旋转 得到线段DP,连结AP,CD,BD.
(1)、求这个二次函数的表达式;(2)、求当 时,y的最大值与最小值的差;(3)、一次函数 的图象与二次函数 的图象交点的横坐标分别是a和b,且 ,求m的取值范围.23. 在 中, , ,点P是平面内不与点A,C重合的任意一点,连接CP,将线段CP绕点P旋转 得到线段DP,连结AP,CD,BD.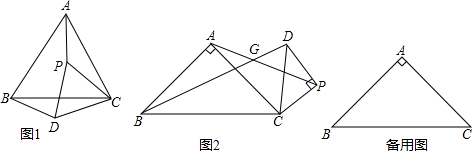 (1)、观察猜想:如图1,当 时,线段CP绕点P顺时针旋转 得到线段DP,则 的值是 , 直线AP与BD相交所成的较小角的度数是;(2)、类比探究:如图2,当 时,线段CP绕点P顺时针旋转 得到线段 请直接写出AP与BD相交所成的较小角的度数,并说明 与 相似,求出 的值;(3)、拓展延伸:当 时,且点P到点C的距离为 ,线段CP绕点P逆时针旋转 得到线段DP,若点A,C,P在一条直线上时,求 的值.
(1)、观察猜想:如图1,当 时,线段CP绕点P顺时针旋转 得到线段DP,则 的值是 , 直线AP与BD相交所成的较小角的度数是;(2)、类比探究:如图2,当 时,线段CP绕点P顺时针旋转 得到线段 请直接写出AP与BD相交所成的较小角的度数,并说明 与 相似,求出 的值;(3)、拓展延伸:当 时,且点P到点C的距离为 ,线段CP绕点P逆时针旋转 得到线段DP,若点A,C,P在一条直线上时,求 的值.