广西玉林市玉州区2021年数学中考模拟试卷(一)
试卷更新日期:2021-04-27 类型:中考模拟
一、单选题
-
1. ﹣1的倒数是( )A、﹣1 B、0 C、1 D、±12. 在Rt△ABC中,已知∠C=90°,AC=4,BC=3,则cosA等于( )A、 B、 C、 D、3. 北京故宫的占地面积约为720 000m2 , 将720 000用科学记数法表示为( ).A、72×104 B、7.2×105 C、7.2×106 D、0.72×1064. 下列四个几何体中,三视图都是相同图形的是( )A、长方体
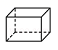 B、圆柱
B、圆柱  C、球
C、球 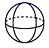 D、三棱柱
D、三棱柱  5. 计算: 的结果是( )A、 B、 C、 D、﹣26. 如图所示, 、 相交于点O,连接 , ,添加下列一个条件后,仍不能判定 的是( )
5. 计算: 的结果是( )A、 B、 C、 D、﹣26. 如图所示, 、 相交于点O,连接 , ,添加下列一个条件后,仍不能判定 的是( ) A、 B、 C、 D、7. 一个不透明袋子中装有1个红球,2个绿球,除颜色外无其他差别.从中随机摸出一个球,然后放回摇匀,再随机摸出一个.下列说法中,错误的是( )A、第一次摸出的球是红球,第二次摸出的球一定是绿球 B、第一次摸出的球是红球,第二次摸出的不一定是红球 C、第一次摸出的球是红球的概率是 D、两次摸出的球都是红球的概率是8. 四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
A、 B、 C、 D、7. 一个不透明袋子中装有1个红球,2个绿球,除颜色外无其他差别.从中随机摸出一个球,然后放回摇匀,再随机摸出一个.下列说法中,错误的是( )A、第一次摸出的球是红球,第二次摸出的球一定是绿球 B、第一次摸出的球是红球,第二次摸出的不一定是红球 C、第一次摸出的球是红球的概率是 D、两次摸出的球都是红球的概率是8. 四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )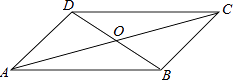 A、AB∥DC,AD∥BC B、AB=DC,AD=BC C、AO=CO,BO=DO D、AB∥DC,AD=BC9. 已知三角形的三边长分别为a,b,c,且a+b=10,ab=18,c=8,则该三角形的形状是( )A、等腰三角形 B、直角三角形 C、钝角三角形 D、等腰直角三角形10. 不等式组 的解集在数轴上表示正确的是( )A、
A、AB∥DC,AD∥BC B、AB=DC,AD=BC C、AO=CO,BO=DO D、AB∥DC,AD=BC9. 已知三角形的三边长分别为a,b,c,且a+b=10,ab=18,c=8,则该三角形的形状是( )A、等腰三角形 B、直角三角形 C、钝角三角形 D、等腰直角三角形10. 不等式组 的解集在数轴上表示正确的是( )A、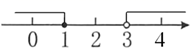 B、
B、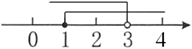 C、
C、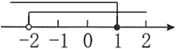 D、
D、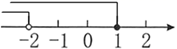 11. 将一张矩形纸片 按如图所示操作:(1)将 沿 向内折叠,使点A落在点 处,(2)将 沿 向内继续折叠,使点P落在点 处,折痕与边 交于点M .
11. 将一张矩形纸片 按如图所示操作:(1)将 沿 向内折叠,使点A落在点 处,(2)将 沿 向内继续折叠,使点P落在点 处,折痕与边 交于点M .若 ,则 的大小是( )
 A、135° B、120° C、112.5° D、115°12. 在平面直角坐标系中,点 是双曲线 上任意一点,连接 ,过点 作 的垂线与双曲线 交于点 ,连接 .已知 ,则 ( )
A、135° B、120° C、112.5° D、115°12. 在平面直角坐标系中,点 是双曲线 上任意一点,连接 ,过点 作 的垂线与双曲线 交于点 ,连接 .已知 ,则 ( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 计算: .14. 计算 所得的结果是.15. 如图,线段 ,用尺规作图法按如下步骤作图.
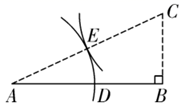
( 1 )过点B作 的垂线,并在垂线上取 ;
( 2 )连接 ,以点C为圆心, 为半径画弧,交 于点E;
( 3 )以点A为圆心, 为半径画弧,交 于点D.即点D为线段 的黄金分割点.
则线段 的长度约为
(结果保留两位小数,参考数据: )
16. 甲、乙两人轮流做下面的游戏:掷一枚均匀的骰子(每个面分别标有1,2,3,4,5,6这六个数字),如果朝上的数字大于3,则甲获胜,如果朝上的数字小于3,则乙获胜,你认为获胜的可能性比较大的是.17. 如图①是山东舰航徽的构图,采用航母45度破浪而出的角度,展现山东舰作为中国首艘国产舰母横空出世的气势,将舰徽中第一条波浪抽象成几何图形,则是一条长为 的弧,若该弧所在的扇形是高为12的圆锥侧面展开图(如图②),则该圆锥的母线长 为.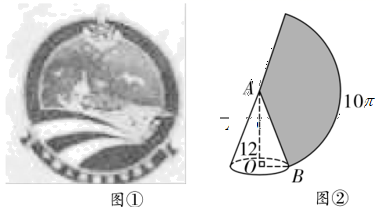 18. 矩形 在平面直角坐标系中的位置如图所示,已知 ,点A在x轴上,点C在y轴上,P是对角线 上一动点(不与原点重合),连接 ,过点P作 ,交x轴于点D.则下列结论正确的是.(写出所有正确结论的序号)
18. 矩形 在平面直角坐标系中的位置如图所示,已知 ,点A在x轴上,点C在y轴上,P是对角线 上一动点(不与原点重合),连接 ,过点P作 ,交x轴于点D.则下列结论正确的是.(写出所有正确结论的序号)
① ;
②当点D运动到 的中点处时, ;
③当 时,点D的坐标为 ;
④在运动过程中, 是一个定值.
三、解答题
-
19. 计算: .20. 解分式方程:21. 已知关于 的一元二次方程 有实数根.(1)、求实数m的取值范围;(2)、当m=2时,方程的根为 ,求代数式 的值.22. 随着科技的进步和网络资源的丰富,在线学习已经成为更多人的自主学习选择.某校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论.为了解学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查(每人只选一类),并根据调查结果绘制成如下两幅不完整的统计图.
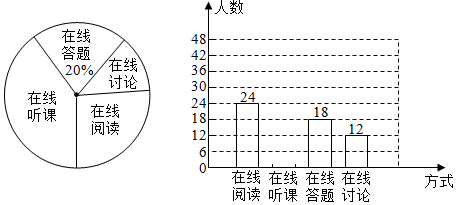
根据图中信息,解答下列问题:
(1)、求本次调查的学生总人数,并补全条形统计图;(2)、求扇形统计图中“在线讨论”对应的扇形圆心角的度数;(3)、该校共有学生2700人,请你估计该校对在线阅读最感兴趣的学生人数.23. 如图,已知 ,以 为直径的 交边 于点E, 与 相切. (1)、若 ,求证: ;(2)、点D是 上一点,点D,E两点在 的异侧.若 , , ,求 半径的长.24. 在“我为祖国点赞”征文活动中,学校计划对获得一、二等奖的学生分别奖励一支钢笔,一本笔记本.已知购买2支钢笔和3个笔记本共38元,购买4支钢笔和5个笔记本共70元.(1)、钢笔、笔记本的单价分别为多少元?(2)、经与商家协商,购买钢笔超过30支时,每增加一支,单价降低0.1元;超过50支,均按购买50支的单价销售.笔记本一律按原价销售.学校计划奖励一、二等奖学生共计100人,其中一等奖的人数不少于30人,且不超过60人,这次奖励一等学生多少人时,购买奖品金额最少,最少为多少元?25. 如图,点E、F、G、H分别在矩形 的边 、 、 、 (不包括端点),上运动,且满足 , .
(1)、若 ,求证: ;(2)、点D是 上一点,点D,E两点在 的异侧.若 , , ,求 半径的长.24. 在“我为祖国点赞”征文活动中,学校计划对获得一、二等奖的学生分别奖励一支钢笔,一本笔记本.已知购买2支钢笔和3个笔记本共38元,购买4支钢笔和5个笔记本共70元.(1)、钢笔、笔记本的单价分别为多少元?(2)、经与商家协商,购买钢笔超过30支时,每增加一支,单价降低0.1元;超过50支,均按购买50支的单价销售.笔记本一律按原价销售.学校计划奖励一、二等奖学生共计100人,其中一等奖的人数不少于30人,且不超过60人,这次奖励一等学生多少人时,购买奖品金额最少,最少为多少元?25. 如图,点E、F、G、H分别在矩形 的边 、 、 、 (不包括端点),上运动,且满足 , . (1)、求证:四边形 是平行四边形;(2)、请探究四边形 的周长一半与矩形 一条对角线长的大小关系,并说明理由.26. 如图,抛物线 经过点 ,与x轴相交于B,C两点,点B在点C的左边.
(1)、求证:四边形 是平行四边形;(2)、请探究四边形 的周长一半与矩形 一条对角线长的大小关系,并说明理由.26. 如图,抛物线 经过点 ,与x轴相交于B,C两点,点B在点C的左边.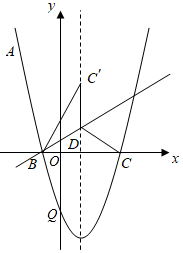 (1)、求抛物线的函数表达式与B,C两点坐标;(2)、点D在抛物线的对称轴上,且位于x轴的上方,将 沿直线 翻折得到 ,若点C恰好落在抛物线的对称轴上,求点C和点D的坐标;(3)、设P是抛物线上位于对称轴右侧的一点,点Q在抛物线的对称轴上,当 为等边三角形时,求直线 的函数表达式.
(1)、求抛物线的函数表达式与B,C两点坐标;(2)、点D在抛物线的对称轴上,且位于x轴的上方,将 沿直线 翻折得到 ,若点C恰好落在抛物线的对称轴上,求点C和点D的坐标;(3)、设P是抛物线上位于对称轴右侧的一点,点Q在抛物线的对称轴上,当 为等边三角形时,求直线 的函数表达式.