广西北部湾经济区2021年数学中考模拟试卷
试卷更新日期:2021-04-27 类型:中考模拟
一、单选题
-
1. 5的相反数是( ).A、 0.2 B、5 C、 D、2. 下列图形中,是轴对称图形,但不是中心对标图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 中国信息通信研究院指出5G对经济社会发展的影响力开始显现,据统计2020年5G将直接带动经济总产出约为8109亿元,将810900000000用科学记数法表示应为( )A、 B、 C、 D、4. 下列事件是必然事件的是( )A、抛掷一枚硬币四次,有两次正面朝上 B、打开电视频道,正在播放新闻 C、射击运动员射击一次,命中十环 D、对顶角相等5. 已知点P(1﹣2a,a﹣1)在第三象限内,则a的取值范围在数轴上表示正确的是( )A、
3. 中国信息通信研究院指出5G对经济社会发展的影响力开始显现,据统计2020年5G将直接带动经济总产出约为8109亿元,将810900000000用科学记数法表示应为( )A、 B、 C、 D、4. 下列事件是必然事件的是( )A、抛掷一枚硬币四次,有两次正面朝上 B、打开电视频道,正在播放新闻 C、射击运动员射击一次,命中十环 D、对顶角相等5. 已知点P(1﹣2a,a﹣1)在第三象限内,则a的取值范围在数轴上表示正确的是( )A、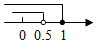 B、
B、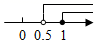 C、
C、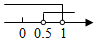 D、
D、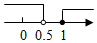 6. 下列计算正确的是( )A、 B、 C、 D、7. 对于任意实数k,关于x的方程x2﹣kx﹣1=0的根的情况为( )A、有两个相等的实数根 B、没有实数根 C、有两个不相等的实数根 D、无法确定8. 如图,在纸上剪一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径r=1,扇形的半径为R,扇形的圆心角等于90°,则R的值是( )
6. 下列计算正确的是( )A、 B、 C、 D、7. 对于任意实数k,关于x的方程x2﹣kx﹣1=0的根的情况为( )A、有两个相等的实数根 B、没有实数根 C、有两个不相等的实数根 D、无法确定8. 如图,在纸上剪一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径r=1,扇形的半径为R,扇形的圆心角等于90°,则R的值是( ) A、R=2 B、R=3 C、R=4 D、R=59. 现代科技的发展已经进入到了5G时代,温州地区将在2021年基本实现5G信号全覆盖.5G网络峰值速率为4G网络峰值速率的10倍,在峰值速率下传输4千兆数据,5G网络比4G网络快360秒.若设4G网络的峰值速率为每秒传输x千兆数据,则由题意可列方程( )A、 — =360 B、 — =360 C、 — =360 D、 — =36010. 计算: 归纳各计算结果中的个位数字规律,猜测 的个位数字是( )A、1 B、3 C、7 D、511. 在同一平面直角坐标系中,函数 与 的图象可能是( )A、
A、R=2 B、R=3 C、R=4 D、R=59. 现代科技的发展已经进入到了5G时代,温州地区将在2021年基本实现5G信号全覆盖.5G网络峰值速率为4G网络峰值速率的10倍,在峰值速率下传输4千兆数据,5G网络比4G网络快360秒.若设4G网络的峰值速率为每秒传输x千兆数据,则由题意可列方程( )A、 — =360 B、 — =360 C、 — =360 D、 — =36010. 计算: 归纳各计算结果中的个位数字规律,猜测 的个位数字是( )A、1 B、3 C、7 D、511. 在同一平面直角坐标系中,函数 与 的图象可能是( )A、 B、
B、 C、
C、 D、
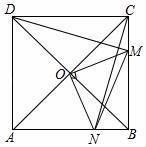
D、 12. 如图,正方形ABCD的对角线AC与BD相交于点O.将∠COB绕点O顺时针旋转,设旋转角为α(0<α<90°),角的两边分别与BC,AB交于点M,N,连接DM,CN,MN,下列四个结论:
12. 如图,正方形ABCD的对角线AC与BD相交于点O.将∠COB绕点O顺时针旋转,设旋转角为α(0<α<90°),角的两边分别与BC,AB交于点M,N,连接DM,CN,MN,下列四个结论:①∠CDM=∠COM;②CN⊥DM;③△CNB≌△DMC;④AN2+CM2=MN2;其中正确结论的个数是( )
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
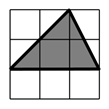
13. 计算( )× =.14. 如图,小明向图中的格盘中随意投掷一枚棋子,该棋子落在三角形内的概率是;
 15. 如图,已知 为四边形 的外接圆,若 ,则 度数为.
15. 如图,已知 为四边形 的外接圆,若 ,则 度数为.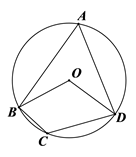 16. 如图,在△ABC中,点D、E分别在边AB、AC上,∠AED=∠B,如果AD=2,AE=3,CE=1,那么BD长为 .
16. 如图,在△ABC中,点D、E分别在边AB、AC上,∠AED=∠B,如果AD=2,AE=3,CE=1,那么BD长为 .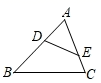 17. 如图,M为双曲线y= 上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于点D、C两点,若直线y=-x+m与y轴交于点A,与x轴相交于点B,则AD•BC的值为 .
17. 如图,M为双曲线y= 上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于点D、C两点,若直线y=-x+m与y轴交于点A,与x轴相交于点B,则AD•BC的值为 . 18. 如图,在边长为1的菱形ABCD中,∠ABC=60°,将△ABD沿射线BD方向平移,得到△EFG,连接EC、GC.求EC+GC的最小值为.
18. 如图,在边长为1的菱形ABCD中,∠ABC=60°,将△ABD沿射线BD方向平移,得到△EFG,连接EC、GC.求EC+GC的最小值为.
三、解答题
-
19. 计算 +| -2|+(3- )0+(-2)2.20. 先化简,再求值: ,其中 .21. 如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中, 的三个顶点 、 、 均在格点上.
 (1)、①将 向下平移5个单位得到 ;
(1)、①将 向下平移5个单位得到 ;②画出 绕点 逆时针旋转 后得到的 ;
(2)、在(1)②的条件下,求 在旋转过程中 扫过的面积.22. “青年大学习”是共青团中央为组织引导广大青少年,深入学习贯彻习近平新时代中国特色社会主义思想和党的十九大精神的青年学校行动,我校为了解同学某季度学习“青年大学习”的情况,从中随机抽取20位同学,并统计学习时间(学习时间用x表示,单位:分钟)收集数据如下:30 56 80 30 40 110 120 156 90 120
58 80 120 140 70 84 10 20 100 86
整理数据:按如下分段整理样本数据并补全表格.
课外阅读时间
人数
4
a
7
b
分析数据:补全下列表格中的统计量.
平均数
中位数
众数
80
c
d
(1)、直接写出上述表格中a,b,c,d的值;(2)、我校有1800名同学参加了此次调查活动,请估计学习时间不低于80分钟的人数是多少?(3)、请从中位数和众数中选择一个量,结合本题解释它的意义.23. (阅读理解)截长补短法,是初中数学几何题中一种辅助线的添加方法,截长就是在长边上载取一条线段与某一短边相等,补短是通过在一条短边上延长一条线段与另一短边相等,从而解决问题.
(1)、如图1,△ABC是等边三角形,点D是边BC下方一点,∠BDC=120°,探索线段DA、DB、DC之间的数量关系.
解题思路:延长DC到点E,使CE=BD.连接AE,根据∠BAC+∠BDC=180°,可证∠ABD=∠ACE,易证得△ABD≌△ACE,得出△ADE是等边三角形,所以AD=DE,从而探寻线段DA、DB、DC之间的数量关系.
根据上述解题思路,请直接写出DA、DB、DC之间的数量关系是
(2)、(拓展延伸)如图2,在Rt△ABC中,∠BAC=90°,AB=AC.若点D是边BC下方一点,∠BDC=90°,探索线段DA、DB、DC之间的数量关系,并说明理由;
(3)、(知识应用)如图3,一副三角尺斜边长都为14cm,把斜边重叠摆放在一起,则两块三角尺的直角顶点之间的距离PQ的长为cm.
24. 正月十五月儿圆,每逢元宵佳节,人们最喜爱在当天进行的活动之一就是与家人一起赏花灯,某商店决定销售一批花灯,经市场调研,某款花灯的进价每个为20元,当售价每个为24元时,周销售量为160个,若售价每提高1元,周销售量就会减少10个,设该款花灯的售价为x元 ,周利润为y元,请解答以下问题:(1)、求y与x的函数关系式?(2)、该商店为了获得周利润750元,且让利给顾客,售价应为多少元?(3)、要求利润不得高于40%,当售价定为多少时,该商店获得利润最大,最大利润是多少元?

