广西北部湾经济区2021年数学中考模拟试卷(一)
试卷更新日期:2021-04-27 类型:中考模拟
一、单选题
-
1. 下列各数中是无理数的是( )A、3.14 B、 C、0.58 D、﹣2. 下列关于防范“新冠肺炎”的标志中既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列事件属于必然事件的是( )A、打开电视,正在播出系列专题片“航拍中国” B、将一组数据中的每一个数都加上同一个数,这组数据的方差不变 C、一个命题的原命题和它的逆命题都是真命题 D、在数轴上任取一点,则这点表示的数是有理数4. 2020年5月22日,李克强总理在政府工作报告中指出:三大攻坚战取得关键进展,农村贫困人口减少 人,贫困发生率降至 脱贫攻坚取得决定性成就.将数字 用科学记数法表示为( )A、 B、 C、 D、5. 将一副三角板按图中方式叠放,则 的度数为( )
3. 下列事件属于必然事件的是( )A、打开电视,正在播出系列专题片“航拍中国” B、将一组数据中的每一个数都加上同一个数,这组数据的方差不变 C、一个命题的原命题和它的逆命题都是真命题 D、在数轴上任取一点,则这点表示的数是有理数4. 2020年5月22日,李克强总理在政府工作报告中指出:三大攻坚战取得关键进展,农村贫困人口减少 人,贫困发生率降至 脱贫攻坚取得决定性成就.将数字 用科学记数法表示为( )A、 B、 C、 D、5. 将一副三角板按图中方式叠放,则 的度数为( )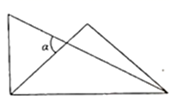 A、 B、 C、 D、6. 下列运算正确的是( )A、a2a3=a6 B、2a+3a=5a2 C、(a+b)2=a2+b2 D、(﹣ab2)3=﹣a3b67. 如图,在△ABC中,AB=AC,以点C为圆心,CB长为半径画弧,交AB于点B和点D,再分别以点B,D为圆心,大于 BD长为半径画弧,两弧相交于点M,作射线CM交AB于点E.若AE=2,BE=1,则EC的长度是( )
A、 B、 C、 D、6. 下列运算正确的是( )A、a2a3=a6 B、2a+3a=5a2 C、(a+b)2=a2+b2 D、(﹣ab2)3=﹣a3b67. 如图,在△ABC中,AB=AC,以点C为圆心,CB长为半径画弧,交AB于点B和点D,再分别以点B,D为圆心,大于 BD长为半径画弧,两弧相交于点M,作射线CM交AB于点E.若AE=2,BE=1,则EC的长度是( )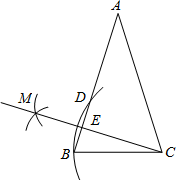 A、2 B、3 C、 D、8. 消费者在网店购物后,将从“好评、中评、差评”中选择一种作为对卖家的评价,假设这三种评价是等可能的,若小明、小亮在某网店购买了同一商品,且都给出了评价,则两人中至少有一个给“好评”的概率为( )A、 B、 C、 D、9. 勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图 , 以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图 的方式放 置在最大正方形内.若图 中阴影部分的面积为 ,且 ,则 的长为( )
A、2 B、3 C、 D、8. 消费者在网店购物后,将从“好评、中评、差评”中选择一种作为对卖家的评价,假设这三种评价是等可能的,若小明、小亮在某网店购买了同一商品,且都给出了评价,则两人中至少有一个给“好评”的概率为( )A、 B、 C、 D、9. 勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图 , 以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图 的方式放 置在最大正方形内.若图 中阴影部分的面积为 ,且 ,则 的长为( )
图1 图2
A、 B、 C、 D、10. 某花圃用花盆培育某种花苗,经过试验发现,每盆花的盈利与每盆株数构成一定的关系.每盆植入3株时,平均单株盈利5元;以同样的栽培条件,若每盆每增加1株,平均单株盈利就减少0.5元.要使每盆的盈利为20元,需要每盆增加几株花苗?设每盆增加 株花苗,下面列出的方程中符合题意的是( )A、 B、 C、 D、11. 如图,已知P为反比例函数y= (x>0)的图象上一点,过点P作PA⊥y轴,PB⊥x轴,E是PA中点,F是BE的中点.若△OPF的面积为3,则k的值为( )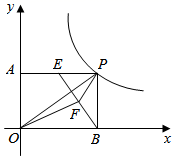 A、6 B、12 C、18 D、2412. 如图,□ABCD的对角线AC,BD相交于点O,E是以A为圆心,以2为半径的圆上一 动点,连结CE,点P为CE的中点,连结BP,若AC= ,BD= ,则BP的最大值为( )
A、6 B、12 C、18 D、2412. 如图,□ABCD的对角线AC,BD相交于点O,E是以A为圆心,以2为半径的圆上一 动点,连结CE,点P为CE的中点,连结BP,若AC= ,BD= ,则BP的最大值为( )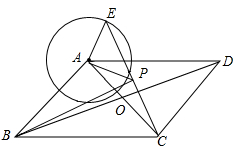 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
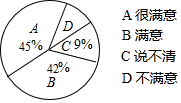
13. 若分式 有意义,则x的取值范围是.14. 计算 =15. 医院为了解医护人员的服务质量,随机调查了来就诊的200名病人,调查的结果如图所示.根据图中给出的信息,这200名顾客中对该医院医护人员的服务质量表示不满意的有人.
 16. 平行四边形的两条邻边的长分别是方程x2﹣7x+1=0的两根,则该平行四边形的周长是.17. 如图,四边形ABCD是正方形,E是边BC上的任意一点,∠AEF=90°,且EF交正方形外角的平分线CF于点F,过点C作CH⊥DF,交DF的延长线于点H.若AB=4,BE= BC,则CH=.
16. 平行四边形的两条邻边的长分别是方程x2﹣7x+1=0的两根,则该平行四边形的周长是.17. 如图,四边形ABCD是正方形,E是边BC上的任意一点,∠AEF=90°,且EF交正方形外角的平分线CF于点F,过点C作CH⊥DF,交DF的延长线于点H.若AB=4,BE= BC,则CH=.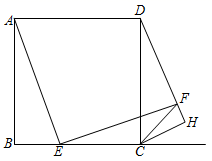 18. 如图,已知扇形AOB的圆心角为120°,点C是半径OA上一点,点D是弧AB上一点.将扇形AOB沿CD对折,使得折叠后的图形恰好与半径OB相切于点 E.若∠OCD=45°,OC= +1,则扇形AOB的半径长是.
18. 如图,已知扇形AOB的圆心角为120°,点C是半径OA上一点,点D是弧AB上一点.将扇形AOB沿CD对折,使得折叠后的图形恰好与半径OB相切于点 E.若∠OCD=45°,OC= +1,则扇形AOB的半径长是.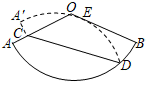
三、解答题
-
19. 计算: .20. 解下列不等式组: ,并写出它的非负整数解.21. △ABC在边长为l的正方形网格中如图所示.
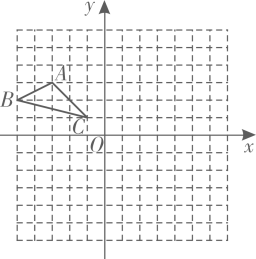
①以点C为位似中心,作出△ABC的位似图形△A1B1C,使其位似比为1:2.且△A1B1C位于点C的异侧,并表示出A1的坐标.
②作出△ABC绕点C顺时针旋转90°后的图形△A2B2C.
③在②的条件下求出点B经过的路径长.
22. 2020年注定是不平凡的一年,新年伊始,一场突如其来的疫情席卷全国,全国人民万众一心,抗战疫情,为了早日取得抗疫的胜利,各级政府、各大新闻媒体都加大了对防疫知识的宣传,某校为了了解初一年级共480名同学对防疫知识的掌握情况,对他们进行了防疫知识测试,现随机抽取甲、乙两班各15名同学的测试成绩(满分100分)进行整理分析,过程如下:(收集数据)
甲班15名学生测试成绩分别为:
78,83,89,97,98,85,100,94,87,90,93,92,99,95,100
乙班15名学生测试成绩中 的成绩如下:91,92,94,90,93
(整理数据)
班级
甲
1
1
3
4
6
乙
1
2
3
5
4
(分析数据)
班级
平均数
众数
中位数
方差
甲
92
93
47.3
乙
90
87
50.2
(应用数据)
(1)、根据以上信息,可以求出: 分, 分;(2)、若规定测试成绩90分及其以上为优秀,请估计参加防疫知识测试的480名学生中成绩为优秀的学生共有多少人;(3)、根据以上数据,你认为哪个班的学生防疫测试的整体成绩较好?请说明理由(一条理由即可).23. 将两张完全相同的矩形纸片 ,矩形纸片 按如图方式放置, 为重合的对角线,重叠部分为四边形 .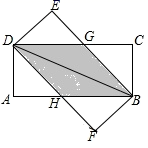 (1)、试判断四边形 为何种特殊的四边形,并说明理由;(2)、若四边形 的面积为15, ,求 的长.24. 受“新冠”疫情影响,全国中小学延迟开学,很多学校都开展起了“线上教学”,市场上对手写板的需求激增.重庆某厂家准备3月份紧急生产A,B两种型号的手写板,若生产20个A型号和30个B型号手写板,共需要投入36000元;若生产30个A型号和20个B型号手写板,共需要投入34000元.(1)、请问生产A,B两种型号手写板,每个各需要投入多少元的成本?(2)、经测算,生产的A型号手写板每个可获利200元,B型号手写板每个可获利400元,该厂家准备用10万元资金全部生产这两种手写板,总获利w元,设生产了A型号手写板a个,求w关于a的函数关系式;(3)、在(2)的条件下,若要求生产A型号手写板的数量不能少于B型号手写板数量的2倍,请你设计出总获利最大的生产方案,并求出最大总获利.25. 如图1,AB是⊙O的直径,点P在⊙O上,且PA=PB,点M是⊙O外一点,MB与⊙O相切于点B,连接OM,过点A作AC∥OM交⊙O于点C,连接BC交OM于点D.
(1)、试判断四边形 为何种特殊的四边形,并说明理由;(2)、若四边形 的面积为15, ,求 的长.24. 受“新冠”疫情影响,全国中小学延迟开学,很多学校都开展起了“线上教学”,市场上对手写板的需求激增.重庆某厂家准备3月份紧急生产A,B两种型号的手写板,若生产20个A型号和30个B型号手写板,共需要投入36000元;若生产30个A型号和20个B型号手写板,共需要投入34000元.(1)、请问生产A,B两种型号手写板,每个各需要投入多少元的成本?(2)、经测算,生产的A型号手写板每个可获利200元,B型号手写板每个可获利400元,该厂家准备用10万元资金全部生产这两种手写板,总获利w元,设生产了A型号手写板a个,求w关于a的函数关系式;(3)、在(2)的条件下,若要求生产A型号手写板的数量不能少于B型号手写板数量的2倍,请你设计出总获利最大的生产方案,并求出最大总获利.25. 如图1,AB是⊙O的直径,点P在⊙O上,且PA=PB,点M是⊙O外一点,MB与⊙O相切于点B,连接OM,过点A作AC∥OM交⊙O于点C,连接BC交OM于点D.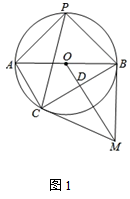 (1)、填空:OD=AC;求证:MC是⊙O的切线;(2)、若OD=9,DM=16,连接PC,求sin∠APC的值;(3)、如图2,在(2)的条件下,延长OB至N,使BN= ,在⊙O上找一点Q,使得 的值最小,请直接写出其最小值为.
(1)、填空:OD=AC;求证:MC是⊙O的切线;(2)、若OD=9,DM=16,连接PC,求sin∠APC的值;(3)、如图2,在(2)的条件下,延长OB至N,使BN= ,在⊙O上找一点Q,使得 的值最小,请直接写出其最小值为.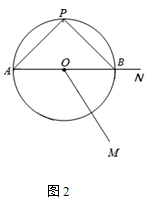 26. 如图,抛物线 与x轴交于A、B两点,与y轴交于点C,已知A(–1,0),且直线BC的解析式为y= x-2,作垂直于x轴的直线 ,与抛物线交于点F,与线段BC交于点E(不与点B和点C重合).
26. 如图,抛物线 与x轴交于A、B两点,与y轴交于点C,已知A(–1,0),且直线BC的解析式为y= x-2,作垂直于x轴的直线 ,与抛物线交于点F,与线段BC交于点E(不与点B和点C重合).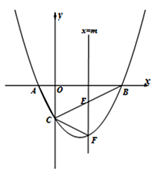 (1)、求抛物线的解析式;(2)、若△CEF是以CE为腰的等腰三角形,求m的值;(3)、点P为y轴左侧抛物线上的一点,过点P作 交直线BC于点M,连接PB,若以P、M、B为顶点的三角形与△ABC相似,求P点的坐标.
(1)、求抛物线的解析式;(2)、若△CEF是以CE为腰的等腰三角形,求m的值;(3)、点P为y轴左侧抛物线上的一点,过点P作 交直线BC于点M,连接PB,若以P、M、B为顶点的三角形与△ABC相似,求P点的坐标.