广西百色市田东县2021年数学中考模拟试卷(一)
试卷更新日期:2021-04-27 类型:中考模拟
一、单选题
-
1. 今年2月份某市一天的最高气温为 ,最低气温为 ,那么这一天的最高气温比最低气温高( )A、 B、 C、 D、2. 式子 有意义的x的取值范围是( )A、 且x≠1 B、x≠1 C、 D、 且x≠13. 下列平面图形中,经过折叠不能围成正方体的是( )A、
 B、
B、 C、
C、 D、
D、 4. 地球的表面积约为510000000km2 , 将510000000用科学记数法表示为( )A、0.51×109 B、5.1×108 C、5.1×109 D、51×1075. 下列计算错误的是( )A、(a3b)•(ab2)=a4b3 B、xy2- xy2= xy2 C、a5÷a2=a3 D、(-mn3)2=m2n56. 有一组数据: ,5, , , , , ,5,则这组数据的众数是( )A、 B、 C、 D、7. 如图,AC∥BD,AD与BC相交于O,∠A=45°,∠B=30°,那么∠AOB等于( )
4. 地球的表面积约为510000000km2 , 将510000000用科学记数法表示为( )A、0.51×109 B、5.1×108 C、5.1×109 D、51×1075. 下列计算错误的是( )A、(a3b)•(ab2)=a4b3 B、xy2- xy2= xy2 C、a5÷a2=a3 D、(-mn3)2=m2n56. 有一组数据: ,5, , , , , ,5,则这组数据的众数是( )A、 B、 C、 D、7. 如图,AC∥BD,AD与BC相交于O,∠A=45°,∠B=30°,那么∠AOB等于( ) A、75° B、60° C、45° D、30°8. 如图,把长方形纸片ABCD沿对角线折叠,设重叠部分为△EBD,那么,有下列说法:①△EBA和△EDC一定是全等三角形;②△EBD是等腰三角形,EB=ED;③折叠后得到的图形是轴对称图形;④折叠后∠ABE和∠CBD一定相等;其中正确的有( )
A、75° B、60° C、45° D、30°8. 如图,把长方形纸片ABCD沿对角线折叠,设重叠部分为△EBD,那么,有下列说法:①△EBA和△EDC一定是全等三角形;②△EBD是等腰三角形,EB=ED;③折叠后得到的图形是轴对称图形;④折叠后∠ABE和∠CBD一定相等;其中正确的有( ) A、1个 B、2个 C、3个 D、4个9. 关于x的一元二次方程 有一个根是0,则k的值是( )A、0 B、1 C、-2 D、1或-210. 由两个可以自由转动的转盘、每个转盘被分成如图所示的几个扇形、游戏者同时转动两个转盘,如果一个转盘转出了红色,另一转盘转出了蓝色,游戏者就配成了紫色,下列说法正确的是( )
A、1个 B、2个 C、3个 D、4个9. 关于x的一元二次方程 有一个根是0,则k的值是( )A、0 B、1 C、-2 D、1或-210. 由两个可以自由转动的转盘、每个转盘被分成如图所示的几个扇形、游戏者同时转动两个转盘,如果一个转盘转出了红色,另一转盘转出了蓝色,游戏者就配成了紫色,下列说法正确的是( ) A、两个转盘转出蓝色的概率一样大 B、如果A转盘转出了蓝色,那么B转盘转出蓝色的可能性变小了 C、游戏者配成紫色的概率为 D、先转动A转盘再转动B转盘和同时转动两个转盘,游戏者配成紫色的概率不同11. 某剧场为希望工程义演的文艺表演有60元和100元两种票价,某团体需购买140张,其中票价为100元的票数不少于票价为60元的票数的两倍,则购买这两种票最少共需要( )A、12120元 B、12140元 C、12160元 D、12200元12. 一个直角三角形的两条直角边的和是14cm,面积是24cm2 , 则其斜边长为( )A、2 cm B、10cm C、8cm D、4 cm
A、两个转盘转出蓝色的概率一样大 B、如果A转盘转出了蓝色,那么B转盘转出蓝色的可能性变小了 C、游戏者配成紫色的概率为 D、先转动A转盘再转动B转盘和同时转动两个转盘,游戏者配成紫色的概率不同11. 某剧场为希望工程义演的文艺表演有60元和100元两种票价,某团体需购买140张,其中票价为100元的票数不少于票价为60元的票数的两倍,则购买这两种票最少共需要( )A、12120元 B、12140元 C、12160元 D、12200元12. 一个直角三角形的两条直角边的和是14cm,面积是24cm2 , 则其斜边长为( )A、2 cm B、10cm C、8cm D、4 cm二、填空题
-
13. 在实数范围内分解因式: =.14. 把直线y=﹣x﹣1沿x轴向右平移1个单位长度,所得直线的函数解析式为.15. 不等式组 的解为.16. 设函数 与 的图象的交点坐标为 ,则 的值为.17. 如图,点D,C的坐标分别为(﹣1,﹣4)和(﹣5,﹣4),抛物线的顶点在线段CD上运动(抛物线随顶点一起平移),与x轴交于A,B两点(A在B的左侧),点B的横坐标最大值为3,则点A的横坐标最小值为.
 18. 如图,把一个面积为1的正方形分成两个面积为 的长方形,再把其中一个面积为 的长方形分成两个面积为 的正方形,再把其中一个面积为 的正方形分成两个面积为 的长方形,如此进行下去……,试用图形揭示的规律计算: .
18. 如图,把一个面积为1的正方形分成两个面积为 的长方形,再把其中一个面积为 的长方形分成两个面积为 的正方形,再把其中一个面积为 的正方形分成两个面积为 的长方形,如此进行下去……,试用图形揭示的规律计算: .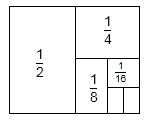
三、解答题
-
19. 计算:(1)、 .(2)、 .20. 先化简,再求值: ÷(1+ ),其中 .21. 如图,一次函数 与反比例函数 的图象相交于 , 两点,连接 , ,延长 交反比例函数图象于点 .
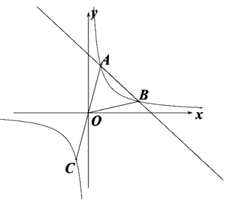 (1)、求一次函数 的表达式与反比例函数 的表达式;(2)、当 时,直接写出自变量 的取值范围为;(3)、点 是 轴上一点,当 时,请直接写出点 的坐标为.22. 在 中, , , 、 分别为边 、 的中点.请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹).
(1)、求一次函数 的表达式与反比例函数 的表达式;(2)、当 时,直接写出自变量 的取值范围为;(3)、点 是 轴上一点,当 时,请直接写出点 的坐标为.22. 在 中, , , 、 分别为边 、 的中点.请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹). (1)、在图1中画一个以点 、点 为顶点的菱形;(2)、在图2中画一个以点 、点 为顶点的矩形.23. 九年级(1)班学生在完成课题学习“体质健康测试中的数据分析”后,利用课外活动时间积极参加体育锻炼,每位同学从篮球、跳绳、立定跳远、长跑、铅球中选一项进行训练.现将项目选择情况作统计图.请你根据上面提供的信息回答下列问题:
(1)、在图1中画一个以点 、点 为顶点的菱形;(2)、在图2中画一个以点 、点 为顶点的矩形.23. 九年级(1)班学生在完成课题学习“体质健康测试中的数据分析”后,利用课外活动时间积极参加体育锻炼,每位同学从篮球、跳绳、立定跳远、长跑、铅球中选一项进行训练.现将项目选择情况作统计图.请你根据上面提供的信息回答下列问题: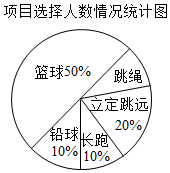 (1)、若选择篮球的人数为20人,则该班共有学生人.(2)、老师决定从选择铅球训练的3名男生和1名女生中任选两名学生先进行测试,请用列表或画树状图的方法求恰好选中两名男生的概率.24. B,D两地间有一段笔直的高速铁路,长度为100km,某时发生的地震对地面上以点A为圆心,30km为半径的圆形区域内的建筑物有影响,分别从B,D两地处测得点A的方位角如图所示,高速铁路是否会受到地震的影响?请通过计算说明理由.(结果精确到0.1km,参考数据: )
(1)、若选择篮球的人数为20人,则该班共有学生人.(2)、老师决定从选择铅球训练的3名男生和1名女生中任选两名学生先进行测试,请用列表或画树状图的方法求恰好选中两名男生的概率.24. B,D两地间有一段笔直的高速铁路,长度为100km,某时发生的地震对地面上以点A为圆心,30km为半径的圆形区域内的建筑物有影响,分别从B,D两地处测得点A的方位角如图所示,高速铁路是否会受到地震的影响?请通过计算说明理由.(结果精确到0.1km,参考数据: )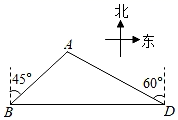 25. 已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.
25. 已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.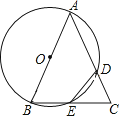 (1)、求证:AB=AC;(2)、若AB=4,BC=2 ,求CD的长.26. 如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N.其顶点为D.
(1)、求证:AB=AC;(2)、若AB=4,BC=2 ,求CD的长.26. 如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N.其顶点为D. (1)、抛物线及直线AC的函数关系式;(2)、若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;(3)、若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.
(1)、抛物线及直线AC的函数关系式;(2)、若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;(3)、若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.