甘肃省兰州市2021年数学中考模拟试卷

试卷更新日期：2021-04-27 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算－3－（－1）的结果是（）

A、－4 B、4 C、－2 D、2

查看试题解析
2. $- 8$ 的立方根为（）

A、2 B、 $- 2$ C、 $\pm 2$ D、 $\pm 4$

查看试题解析
3. 如图，a $//$ b，且∠1＝60°，则∠2＝（）

A、30° B、45° C、60° D、120°

查看试题解析
4. 化简 $\frac{2}{x^{2} - 1}$ ÷ $\frac{1}{x - 1}$ 的结果是（）

A、 $\frac{2}{x + 1}$ B、 $\frac{2}{x}$ C、 $\frac{2}{x - 1}$ D、2（x+1）

查看试题解析
5. 如图，等腰三角形ABC中，AB＝AC，∠A＝46°，CD⊥AB于点D，则∠DCB＝（）

A、46° B、67° C、44° D、23°

查看试题解析
6. 已知△ABC∽△DEF，相似比为2，且△ABC的面积为16，则△DEF的面积为（）

A、32 B、8 C、4 D、16

查看试题解析
7. 一次函数 $y = x - 3$ 的图象经过（）

A、第一、二、三象限 B、第一、二、四象限 C、第二、三、四象限 D、第一、三、四象限

查看试题解析
8. 已知圆内接正六边形的半径为2，则该内接正六边形的边心距为（）

A、2 B、1 C、 $\sqrt{3}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
9. 《九章算术》中记载：“今有甲乙二人持钱不知其数.甲得乙半而钱五十，乙得甲太半而亦钱五十.问：甲、乙持钱各几何？”大意是：甲、乙二人带着钱，不知是多少，若甲得到乙的钱数的 $\frac{1}{2}$ ，则甲的钱数为50；若乙得到甲的钱数的 $\frac{2}{3}$ ，则乙的钱数也能为50，问甲、乙各有多少钱？设甲持钱为x，乙持钱为y，可列方程组为（）

A、 ${\begin{array}{l} x + \frac{2}{3} y = 50 \\ y + \frac{1}{2} x = 50 \end{array}$ B、 ${\begin{array}{l} x + \frac{1}{2} y = 50 \\ y + \frac{2}{3} x = 50 \end{array}$ C、 ${\begin{array}{l} x - \frac{1}{2} y = 50 \\ y - \frac{2}{3} x = 50 \end{array}$ D、 ${\begin{array}{l} x - \frac{2}{3} y = 50 \\ y - \frac{1}{2} x = 50 \end{array}$

查看试题解析
10. 如图△ABC中，∠BAC=90°，将△ABC绕点A按顺时针方向旋转一定角度得到△ADE，点B的对应点D恰好落在BC边上，若AC=4 $\sqrt{3}$ ，∠B=60°，则CD的长为（）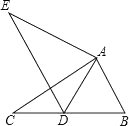

A、2 B、4 C、6 D、2 $\sqrt{3}$

查看试题解析
11. 如图， $A B ⊥ O A$ 于点A，AB交反比例函数 $y = \frac{k}{x}$ （x＜0）的图象于点C，且 $A C ∶ B C ＝ 1 ∶ 3$ ，若 $S_{△ A O B} ＝ 4$ ，则k＝（）

A、4 B、﹣4 C、2 D、﹣2

查看试题解析
12. 如图，在△ABC中，∠A＝90°，AB＝6，AC＝8，以点B为圆心，小于AB的长为半径画弧，分别交AB，BC于D，E两点，再分别以点D和点E为圆心，大于 $\frac{1}{2}$ DE的长为半径画弧，两弧交于点F，射线BF交AC于点G，则tan∠CBG＝（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{3}{4}$ D、 $\frac{4}{3}$

查看试题解析

二、填空题

13. 因式分解： $x^{3} ﹣ 2 x^{2} y + x y^{2} =$ ．

查看试题解析
14. 若点A（﹣2，y₁）和B（1，y₂）是二次函数y＝x²﹣4x﹣3图象上的两点，则y₁y₂.（填“＜”“＝”或“＞”）

查看试题解析
15. 转动如图所示的两个转盘（每个转盘被分成五个面积相等的扇形）各一次，两次转得的数字之和大于7的概率是.

查看试题解析
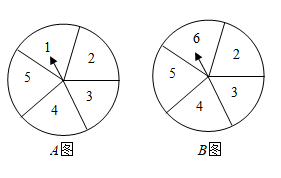16. 如图，在菱形ABCD中，AB＝3，AF⊥BC于点F，FC＝2，AF与DB交于点N，则AN＝.

查看试题解析

17. 民以食为天，农产品是关系国计民生的重要商品，是事关经济发展、社会稳定和国家自立的头等大事，某数学兴趣小组为了解我国近几年人均主要农产品产量情况，该组成员通过对我国粮食、猪羊牛肉的人均产量进行收集、整理、描述和分析，下面给出部分信息.

信息一、2005﹣2019年我国人均粮食产量统计图：

信息二、将2005﹣2019年划分为三个时间段，每个时间段内我国人均粮食产量如下：

时间段	2005﹣2009	2010﹣2014	2015﹣2019
平均数/千克	388.4	448.4	477

信息三、2019年我国各省、市、自治区粮食、猪羊牛肉的人均产量的统计量如下：

统计量类别	平均数	中位数	极差
人均粮食产量/千克	475	419	1981
人均猪羊牛肉产量/千克	40	42.5	91.5

（以上数据来源于《2020中国统计年鉴》）

根据以上信息，解决下列问题：

(1)、2019年甘肃省人均粮食产量为440千克，人均猪羊牛肉产量为36.2千克，甘肃省这两项主要农产品产量排名更靠前的是（填“人均粮食产量”或“人均猪羊牛肉产量”），理由是：.

(2)、根据以上数据信息分析，判断下列结论正确的是：（只填序号）

①2005﹣2015年内我国人均粮食产量呈现持续增长趋势；

②2005﹣2019年划分的三个时间段中，2010﹣2014年人均粮食产量的平均增长率最高；

③2005﹣2019年我国人均粮食产量连续12年高于人均400千克的国际粮食安全标准线.

(3)、记我国2005﹣2009年人均粮食产量的方差为

S_{1}^{2}

，2015﹣2019年人均粮食产量的方差为

S_{2}^{2}

，则

S_{1}^{2}

S_{2}^{2}

.（填＜、＝或＞）

查看试题解析

三、解答题

18. 用配方法解方程： $x^{2} + 27 = 12 x$ .

查看试题解析
19. 先化简，再求值：m（2n+m）﹣（1+m）²+2m，其中m＝﹣ $\frac{1}{2}$ ，n＝6.

查看试题解析
20. 解不等式组： ${\begin{matrix} \frac{x - 1}{2} < \frac{x}{3} \\ 3 (x + 2) \geq 2 x + 5 \end{matrix}$

查看试题解析
21. 如图，在等边三角形ABC中，AD＝BE.求证：CD＝AE.

查看试题解析

22. 兰州市居民用电现有两种用电收费方式：

智能分时电表		普通电表
峰时（8：00﹣22：00）	谷时（22：00﹣次日8：00）	电价0.51/千瓦时
电价0.76元/千万时	电价0.26元/千瓦时	电价0.51/千瓦时

设某家庭某月用电总量为x千瓦时，其中谷时用电60千瓦时，则峰时用电（x﹣60）千瓦时，智能分时电表计价时的总价为为y₁（元），普通电表计价时的总价为y₂（元）.请分别写出两种电表计价时的总价与用电总量之间的函数关系式.

查看试题解析

23. 如图，海中有一个小岛A，该岛四周10海里内有暗礁，一艘货轮由西向东航行，开始在A岛南偏西58°的B处，往东行驶10海里后到达A岛西南方向的C处.货轮如继续向东航行是否有触礁的危险？（参考数据：sins58°≈0.85，cos58°≈0.53，tan58°≈1.60）

查看试题解析
24. 如图，在平面直角坐标系 $x O y$ 中，反比例函数 $y = \frac{k}{x}$ （x＞0）与一次函数 $y = - x + b$ 的图象交于A，B（4，1）两点.

(1)、求一次函数 $y = - x + b$ 和反比例函数 $y = \frac{k}{x}$ （x＞0）的表达式；

(2)、求△AOB的面积.

查看试题解析

25. 如图，点C为弦AB上的一定点，AB＝6.4cm.

\overset{⌢}{A B}

上有一动点D，连接CD，将CD绕点C逆时针旋转60°得到CE，连接EA，ED，AD.

小军尝试结合学习函数的经验，对线段AD，CD，AE的长度之间的关系进行了探究，请将以下小军的探究过程补充完整.

(1)、列表：下表的数据是根据点D在

\overset{⌢}{A B}

上的不同位置进行画图，通过测量线段AD，CD，AE的长度，分别得到了几组对应值：

位置线段	①	②	③	④	⑤	⑥	⑦	⑧
AD/cm	0.00	0.83	1.60	2.36	3.40	4.51	5.40	6.40
CD/cm	3.00	2.51	2.10	1.76	1.60	1.93	2.51	3.40
AE/cm	3.00	2.20	1.57	1.28	1.80	3.00	4.12	5.55

在AD，CD，AE的长度这三个量中，确定的长度是自变量x，另外两条线段的长度都是这个自变量的函数y；

(2)、描点、连线：在同一平面直角坐标系xOy中，画出（1）中所确定的两个函数的图象；

(3)、解决问题：在点D的运动过程中，当CD＝AE时，求AD的大约长度.（结果保留两位小数）

查看试题解析

26. 如图，在Rt△ABC中，∠C＝90°，以AB上一点O为圆心，OA的长为半径作⊙O，交AC，AB分别于D，E两点，连接BD，且∠A＝∠CBD.

(1)、求证：BD是⊙O的切线；

(2)、若CD＝1，BC＝2，求⊙O的半径.

查看试题解析
27. 探索与应用：如图

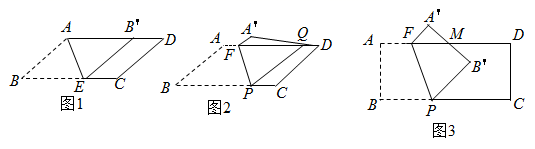(1)、问题解决：如图1.在平行四边形纸片ABCD（AD＞AB）中，将纸片沿过点A的直线折叠，使点B落在AD上的点 $B^{'}$ 处，折线AE交BC于点E，连接B'E.求证：四边形 $A B E B^{'}$ 是菱形.

(2)、规律探索：如图2，在平行四边形纸片ABCD（AD＞AB）中，将纸片沿过点P的直线折叠，点B恰好落在AD上的点Q处，点A落在点A′处，得到折痕FP，那么△PFQ是等腰三角形吗？请说明理由.

(3)、拓展应用：如图3，在矩形纸片ABCD（AD＞AB）中，将纸片沿过点P的直线折叠，得到折痕FP，点B落在纸片ABCD内部点 $B^{'}$ 处，点A落在纸片ABCD外部点 $A^{'}$ 处， $A^{'} B^{'}$ 与AD交于点M，且 $A^{'}$ M＝ $B^{'}$ M.已知：AB＝4，AF＝2，求BP的长.

查看试题解析
28. 如图1，抛物线y＝ax²﹣5x+c与直线y＝﹣x+4相交于A（4，0），B（0，4）两点.动点C从点O出发，以每秒1个单位长度的速度沿OA方向运动，设运动的时间为t秒.过点C作CD⊥x轴分别交直线AB于点D，抛物线于点E.

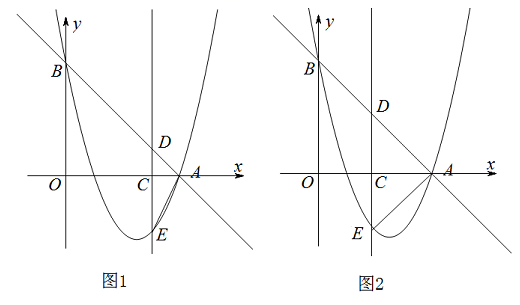(1)、求抛物线y＝ax²﹣5x+c的表达式；

(2)、连接AE，当t＝3时，求△ADE的面积；

(3)、如图2.当t＝2时，在x轴上存在点F，抛物线上存在点G，直线DE上存在点H，当以C，F，G，H为顶点的四边形是正方形时，求点F的坐标.

查看试题解析