甘肃省白银市2021年数学中考模拟试卷
试卷更新日期:2021-04-27 类型:中考模拟
一、单选题
-
1. 有下列各数:0.456, ,(﹣π)0 , 3.14,0.80108,0.1010010001…(相邻两个1之间0的个数逐次加1), , ,其中是无理数的有( )A、1个 B、2个 C、3个 D、4个2. 将一副直角三角尺按如图所示的不同方式摆放,则图中锐角∠α与∠β相等的是( )A、
 B、
B、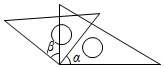 C、
C、 D、
D、 3. ( )A、 B、 C、8 D、44. 下列几何体中,主视图是长方形的是( )A、
3. ( )A、 B、 C、8 D、44. 下列几何体中,主视图是长方形的是( )A、 B、
B、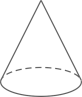 C、
C、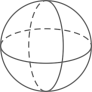 D、
D、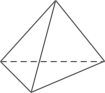 5. 下列计算正确的是( )A、 B、 C、 D、6. 已知一次函数 的图象经过点A,且y随x的增大而减小,则点A的坐标可以是( )A、 B、 C、 D、7. 已知 是一元二次方程 的一个根,则m的值为( )A、-1或2 B、-1 C、2 D、08. 如图,菱形ABCD中,∠A=60°,边AB=8,E为边DA的中点,P为边CD上的一点,连接PE、PB,当PE=EB时,线段PE的长为( )
5. 下列计算正确的是( )A、 B、 C、 D、6. 已知一次函数 的图象经过点A,且y随x的增大而减小,则点A的坐标可以是( )A、 B、 C、 D、7. 已知 是一元二次方程 的一个根,则m的值为( )A、-1或2 B、-1 C、2 D、08. 如图,菱形ABCD中,∠A=60°,边AB=8,E为边DA的中点,P为边CD上的一点,连接PE、PB,当PE=EB时,线段PE的长为( ) A、4 B、8 C、4 D、49. 如图, 是半圆 的直径, ,点 , 在半圆上, , ,点 是 上的一个动点,则 的最小值为( )
A、4 B、8 C、4 D、49. 如图, 是半圆 的直径, ,点 , 在半圆上, , ,点 是 上的一个动点,则 的最小值为( ) A、 B、 C、 D、10. 如图①,AB=5,射线AM BN,点C在射线BN上,将△ABC沿AC所在直线翻折,点B的对应点D落在射线BN上,点P,Q分别在射线AM、BN上,PQ AB.设AP=x,QD=y.若y关于x的函数图象(如图②)经过点E(9,2),则cosB的值等于( )
A、 B、 C、 D、10. 如图①,AB=5,射线AM BN,点C在射线BN上,将△ABC沿AC所在直线翻折,点B的对应点D落在射线BN上,点P,Q分别在射线AM、BN上,PQ AB.设AP=x,QD=y.若y关于x的函数图象(如图②)经过点E(9,2),则cosB的值等于( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 2020年6月9日,我国全海深自主遥控潜水器“海斗一号”在马里亚纳海沟刷新了我国潜水器下潜深度的纪录,最大下潜深度达10907米.假设以马里亚纳海沟所在海域的海平面为基准,记为0米,高于马里亚纳海沟所在海域的海平面100米的某地的高度记为 米,根据题意,“海斗一号”下潜至最大深度10907米处,该处的高度可记为米.12. 分解因式:x2(x﹣3)﹣x+3=.13. 已知A、B两地相距1000米,甲、乙两人分别从A、B两地同时出发,沿着同一条直线公路相向而行.若甲以7米/秒的速度骑自行车前进,乙以3米/秒的速度步行,则经过秒两人相距100米.14. 当x时,分式 有意义.15. 某射手在同一条件下进行射击,结果如下表所示:
射击次数( )
10
20
50
100
200
500
…
击中靶心次数( )
8
17
45
92
182
453
…
击中靶心频率( )
0.80
0.85
0.90
0.92
0.91
0.905
…
由此表估计这个射手射击1次,击中靶心的概率是.(保留一位小数)
16. 将点 向上平移2个单位长度得到点Q,则点Q的坐标为 .17. 一个扇形的圆心角为 ,它的面积是 ,则这个扇形的弧长为 .18. 观察下列各式:;
;
;
……
请利用你发现的规律,计算 ,其结果为.
三、解答题
-
19. 计算: .20. 解不等式组 .21. 如图,在 中,D是 边上一点,且 .
 (1)、尺规作图(保留作图痕迹,不写作法)
(1)、尺规作图(保留作图痕迹,不写作法)①作 的角平分线交 于点E;
②作线段 的垂直平分线交 于点F.
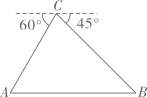
(2)、连接 ,直接写出线段 和 的数量关系及位置关系.22. 某校“综合与实践”小组采用无人机辅助的方法测量一座桥的长度.如图,桥 是水平并且笔直的,测量过程中,小组成员遥控无人机飞到桥 的上方120米的点C处悬停,此时测得桥两端A,B两点的俯角分别为60°和45°,求桥 的长度.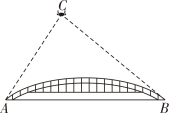
 23. 2019年甘肃在国际知名旅游指南《孤独星球》亚洲最佳旅游地排名第一,截至2020年1月,甘肃省已有五家国家5A级旅游景区,分别为A:嘉峪关文物景区;B:平凉崆峒山风景名胜区;C:天水麦积山景区;D:敦煌鸣沙月牙泉景区:E:张掖七彩舟霞景区,张帆同学与父母计划在暑假期间从中选择部分景区游玩.(1)、张帆一家选择E:张掖七彩丹霞景区的概率是多少?(2)、若张帆一家选择了E:张掖七彩丹霞景区,他们再从A,B,C,D四个景区中任选两个景区去旅游,求选A,D两个景区的概率(要求画树状图或列表求概率).24. 为了让青少年学生走向操场,走进自然,走到阳光下,积极参加体育锻炼.我校启动了“学生阳光体育运动”短跑运动,可以锻炼人的灵活性,增强人的爆发力,因此小明和小亮在课外活动中,报名参加了短跑训练小组.在近几次百米训练中,所测成绩如图所示,请根据图中所示解答以下问题.
23. 2019年甘肃在国际知名旅游指南《孤独星球》亚洲最佳旅游地排名第一,截至2020年1月,甘肃省已有五家国家5A级旅游景区,分别为A:嘉峪关文物景区;B:平凉崆峒山风景名胜区;C:天水麦积山景区;D:敦煌鸣沙月牙泉景区:E:张掖七彩舟霞景区,张帆同学与父母计划在暑假期间从中选择部分景区游玩.(1)、张帆一家选择E:张掖七彩丹霞景区的概率是多少?(2)、若张帆一家选择了E:张掖七彩丹霞景区,他们再从A,B,C,D四个景区中任选两个景区去旅游,求选A,D两个景区的概率(要求画树状图或列表求概率).24. 为了让青少年学生走向操场,走进自然,走到阳光下,积极参加体育锻炼.我校启动了“学生阳光体育运动”短跑运动,可以锻炼人的灵活性,增强人的爆发力,因此小明和小亮在课外活动中,报名参加了短跑训练小组.在近几次百米训练中,所测成绩如图所示,请根据图中所示解答以下问题. (1)、请根据图中信息,补齐下面的表格:
(1)、请根据图中信息,补齐下面的表格:次数
1
2
3
4
5
小明
13.3
13.4
13.3
13.3
小亮
13.2
13.1
13.5
13.3
(2)、分别写出他们的中位数和众数;(3)、分别计算他们的平均数和方差,将小明与小亮的成绩比较后,你将分别给予他们怎样的建议?25. 已知y是x的函数,自变量x的取值范围是全体实数,下表是y与x的几组对应值x
…
﹣4
﹣3
﹣2
﹣1
﹣
0
1
2
3
4
…
y
…
5
0
﹣3
﹣4
﹣
﹣3
﹣
﹣4
﹣3
0
5
…
小京根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小京的探究过程,请补充完整:
(1)、如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象; (2)、根据画出的函数图象,写出:
(2)、根据画出的函数图象,写出:①x= 对应的函数值y约为;
②该函数的一条性质:.
26. 如图,在菱形ABCD中,P为对角线AC上一点,AB与经过A、P、D三点的⊙O相切于点A. (1)、求证:AP=DP;(2)、若AC=8,tan∠BAC= ,求⊙O的半径.27.(1)、如图1,在正方形ABCD中,EF分别是BC,CD上的点,且∠EAF=45°,探究图中线段BE,EF,FD之间的数量关系.小王同学探究此问题的方法是将△ABE绕A点旋转90°使得B与D重合,连接AG,由此得到 , 再证明 , 可得出结论,他的结论应是.
(1)、求证:AP=DP;(2)、若AC=8,tan∠BAC= ,求⊙O的半径.27.(1)、如图1,在正方形ABCD中,EF分别是BC,CD上的点,且∠EAF=45°,探究图中线段BE,EF,FD之间的数量关系.小王同学探究此问题的方法是将△ABE绕A点旋转90°使得B与D重合,连接AG,由此得到 , 再证明 , 可得出结论,他的结论应是. (2)、拓展延伸:
(2)、拓展延伸:如图2,等腰直角三角形ABC中,∠ABC=90°,AB=BC,点G,H在边AC上,且∠GBH=45°,写出图中线段AG,GH,CH之间的数量关系并证明.
28. 如图,抛物线L:y= x2﹣ x﹣3与x轴正半轴交于点A,与y轴交于点B. (1)、求直线AB的解析式及抛物线顶点坐标;(2)、如图1,点P为第四象限抛物线上一动点,过点P作PC⊥x轴,垂足为C,PC交AB于点D,求PD+ AD的最大值,并求出此时点P的坐标;(3)、如图2,将抛物线L:y= x2﹣ x﹣3向右平移得到抛物线L′,直线AB与抛物线L′交于M,N两点,若点A是线段MN的中点,求抛物线L′的解析式.
(1)、求直线AB的解析式及抛物线顶点坐标;(2)、如图1,点P为第四象限抛物线上一动点,过点P作PC⊥x轴,垂足为C,PC交AB于点D,求PD+ AD的最大值,并求出此时点P的坐标;(3)、如图2,将抛物线L:y= x2﹣ x﹣3向右平移得到抛物线L′,直线AB与抛物线L′交于M,N两点,若点A是线段MN的中点,求抛物线L′的解析式.