浙江省杭州市七县区(建德、桐庐、淳安、富阳、临安、余杭、萧山)2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-04-27 类型:期末考试
一、单选题
-
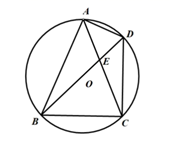
1. 抛物线 的顶点坐标( )A、 B、 C、 D、2. 下列事件中,属于不可能事件的是( )A、a是实数,则|a|≥0 B、任意一个三角形都有外接圆 C、抛掷一枚骰子,朝上面的点数是6 D、一匹马奔跑的速度是每秒100米3. 若 ,则 ( )A、 B、 C、 D、4. 如图,在 中,AB、CD是 的直径,若 ,则∠C=( )
 A、20° B、35° C、55° D、70°5. 如图,在 中,D,E分别是边AB,BC上的点,且 ,若BE:CE=1:3,则 的值为( )
A、20° B、35° C、55° D、70°5. 如图,在 中,D,E分别是边AB,BC上的点,且 ,若BE:CE=1:3,则 的值为( ) A、 B、 C、 D、6. 将抛物线 : 向右平移3个单位,再向上平移2个单位得到抛物线 ,则抛物线 的函数表达式为( )A、 B、 C、 D、7. 数轴上有两个点A和B,点B表示实数6,点A表示实数a, 半径为4.若点A在 内,则( )A、 或 B、 C、 D、8. 下列不等式成立的是( )A、sin60° sin45° sin30° B、cos30° cos45° cos60° C、tan60° tan45° tan30° D、sin30° cos45° tan60°9. 如图一个扇形纸片的圆心角为90°,半径为6,将这张扇形纸片折叠,使点A和点O恰好重合,折痕为CD,则阴影部分的面积为( )
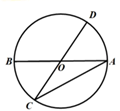
A、 B、 C、 D、6. 将抛物线 : 向右平移3个单位,再向上平移2个单位得到抛物线 ,则抛物线 的函数表达式为( )A、 B、 C、 D、7. 数轴上有两个点A和B,点B表示实数6,点A表示实数a, 半径为4.若点A在 内,则( )A、 或 B、 C、 D、8. 下列不等式成立的是( )A、sin60° sin45° sin30° B、cos30° cos45° cos60° C、tan60° tan45° tan30° D、sin30° cos45° tan60°9. 如图一个扇形纸片的圆心角为90°,半径为6,将这张扇形纸片折叠,使点A和点O恰好重合,折痕为CD,则阴影部分的面积为( )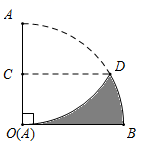 A、 B、 C、 D、10. 已知二次函数 与x轴只有一个交点,且图象经过两点A(1,n),B(m+2,n),则m、n满足的关系为( )A、 B、 C、 D、
A、 B、 C、 D、10. 已知二次函数 与x轴只有一个交点,且图象经过两点A(1,n),B(m+2,n),则m、n满足的关系为( )A、 B、 C、 D、二、填空题
-
11. tanA=1,则锐角∠A=.12. 某射手在同一条件下进行射击,结果如下表所示:
射击次数( )
10
20
50
100
200
500
…
击中靶心次数( )
8
17
45
92
182
453
…
击中靶心频率( )
0.80
0.85
0.90
0.92
0.91
0.905
…
由此表估计这个射手射击1次,击中靶心的概率是.(保留一位小数)
13. 已知圆心角为60°的扇形的弧长为 ,则扇形的半径为.14. 已知在 中,∠B=36°,AB=AC,D为BC上一点,满足AD=CD,则 =.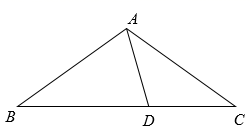 15. 如图,在平面直角坐标系中,抛物线 与y轴交于点A,过点A作x轴的平行线交抛物线于点M,P为抛物线的顶点,若直线OP交直线AM于点B,且M为线段AB的中点,则a的值为.
15. 如图,在平面直角坐标系中,抛物线 与y轴交于点A,过点A作x轴的平行线交抛物线于点M,P为抛物线的顶点,若直线OP交直线AM于点B,且M为线段AB的中点,则a的值为.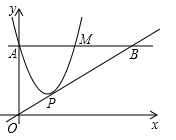 16. 如图, 内接于 ,∠BAC=70°,D是BC的中点,且∠AOD=156°,AE,CF分别是BC,AB边上的高,则∠BCF的度数是.
16. 如图, 内接于 ,∠BAC=70°,D是BC的中点,且∠AOD=156°,AE,CF分别是BC,AB边上的高,则∠BCF的度数是.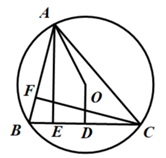
三、解答题
-
17. 设有3个型号相同的杯子,其中一等品2个,二等品1个.从中任取1个杯子,记下等级后放回,第二次再从中取1个杯子.求:(1)、第一次取出的杯子是一等品的概率.(2)、用树状图或列表的方法求两次取出都是一等品的概率.18. 如图,在矩形ABCD中,BE交AD于点E且平分∠ABC,对角线BD平分∠EBC.
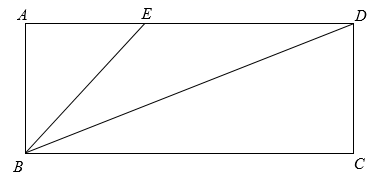 (1)、求 的值.(2)、求 .19. 将图中的破轮子复原,已知弧上三点A,B,C.
(1)、求 的值.(2)、求 .19. 将图中的破轮子复原,已知弧上三点A,B,C. (1)、用尺规作出该轮的圆心O,并保留作图痕迹;(2)、若 是等腰三角形,设底边 ,腰 ,求圆片的半径R.20. 商店销售某商品,销售中发现,该商品每天的销售量y(个)与销售单价x(元/个)之间存在如图所示的关系,其中成本为20元/个.
(1)、用尺规作出该轮的圆心O,并保留作图痕迹;(2)、若 是等腰三角形,设底边 ,腰 ,求圆片的半径R.20. 商店销售某商品,销售中发现,该商品每天的销售量y(个)与销售单价x(元/个)之间存在如图所示的关系,其中成本为20元/个.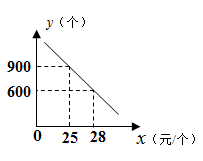 (1)、求y与x之间的函数关系式.(2)、为了保证每天利润不低于1300元,单价不高于30元/个,那么商品的销售单价应该定在什么范围?21. 如图,在 中,∠ACB=90°,AC=BC,O是AB的中点,连结OC,点F,E分别在边AB和BC上,过E点作EM⊥AB,垂足为M,满足∠FCO=∠EFM.
(1)、求y与x之间的函数关系式.(2)、为了保证每天利润不低于1300元,单价不高于30元/个,那么商品的销售单价应该定在什么范围?21. 如图,在 中,∠ACB=90°,AC=BC,O是AB的中点,连结OC,点F,E分别在边AB和BC上,过E点作EM⊥AB,垂足为M,满足∠FCO=∠EFM.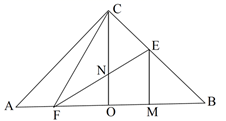 (1)、求证:CF=EF;(2)、求证: .
(1)、求证:CF=EF;(2)、求证: .