江苏省淮安市淮安区2021届九年级上学期数学期末考试试卷

试卷更新日期：2021-04-27 类型：期末考试

进入 出卷网 下载

一、单选题

  • 1. 方程x2＝x的根是（ ）
    A、x＝0 B、x＝1 C、x＝0 或x＝1 D、x＝0 或x＝﹣1

    查看试题解析

  • 2. 已知⊙O的直径为4，点O到直线m的距离为2，则直线m与⊙O的位置关系是（　　）
    A、相交 B、相切 C、相离 D、无法判断

    查看试题解析

  • 3. 分别写有数字0，﹣1，﹣2，1，3的五张卡片，除数字不同外其他均相同，从中任抽一张，那么抽到负数的概率是（　　）

    A、15 B、25 C、35 D、45

    查看试题解析

  • 4. 如图，点A，B，C都在⊙O上，若∠ABC＝60°，则∠AOC的度数是（   ）

    A、100° B、110° C、120° D、130°

    查看试题解析

  • 5. 数据3、4、6、7、x的平均数是5，这组数据的中位数是（   ）
    A、4 B、4.5 C、5 D、6

    查看试题解析

  • 6. 关于 x 的一元二次方程 x2−2x+m=0 无实数根，则实数 m 的取值范围是（  ）
    A、m<1 B、m≥1 C、m≤1 D、m>1

    查看试题解析

  • 7.

    如图，在△ABC中，D、E分别是AB、AC的中点，下列说法中不正确的是（　　）


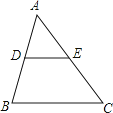    A、DE= 12 BC B、ADAB=AEAC C、△ADE∽△ABC D、S△ADE：S△ABC=1：2

    查看试题解析

  • 8. 已知二次函数 y=ax2+bx+c 的图象如图所示，则下列结论正确的个数有（　　）

    ① c>0 ；② b2−4ac<0 ；③ a−b+c>0 ；④当 x>1 时，y随x的增大而减小

    A、4个 B、3个 C、2个 D、1个

    查看试题解析

二、填空题

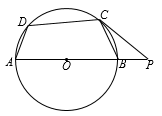
  • 9. 若2a=3b，则a:b=.

    查看试题解析

  • 10. 在一次射击比赛中，甲、乙两名运动员10次射击的平均成绩都是7环，其中甲的成绩的方差为1.2，乙的成绩的方差为3.9，由此可知 的成绩更稳定．

    查看试题解析

  • 11. 已知x＝1是一元二次方程x2﹣mx+1＝0的一个解，则m的值是.

    查看试题解析

  • 12. 抛物线 y=(x−2)2+1 的顶点坐标是.

    查看试题解析

  • 13. 将二次函数 y=2x2 的图象向右平移2个单位长度，再向上平移3个单位长度，得到的图象所对应的函数表达式为.

    查看试题解析

  • 14. 圆锥的底面半径为5cm，侧面展开图的面积是30πcm2 ， 则该圆锥的母线长为cm

    查看试题解析

  • 15. 如图，四边形ABCD内接于⊙O，AB是⊙O的直径，过点C作⊙O的切线交AB的延长线于点P，若∠P＝40°，则∠ADC＝°．

    查看试题解析

  • 16. 如图，在矩形纸片ABCD中，边AB=12，AD=5，点P为DC边上的动点（点P不与点D，C重合，将纸片沿AP折叠，则CD′的最小值为.

    查看试题解析

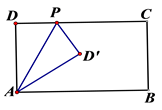
三、解答题

  • 17. 解方程
    (1)、（x-1）2 ＝4        
    (2)、x2﹣6x﹣7＝0；

    查看试题解析

  • 18. 如图，AB是圆O的直径，AD是弦，∠DAB＝22.5°，过点D作圆O的切线DC交AB的延长线于点C.

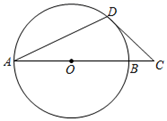    (1)、求∠C的度数；
    (2)、若AB＝2 2 ，求BC的长度.

    查看试题解析

  • 19. 为了从小华和小亮两人中选拔一人参加射击比赛，现对他们的射击水平进行测试，两人在相同条件下各射击6次，命中的环数如下（单位：环）：

    小华：7，8，7，8，9，9；          小亮：5，8，7，8，10，10.

    (1)、填写下表：

    平均数（环）

    中位数（环）

    方差（环2）

    小华

     

    8

     

    小亮

    8

     

    3
    (2)、根据以上信息，你认为教练会选择谁参加比赛，理由是什么？
    (3)、若小亮再射击2次，分别命中7环和9环，则小亮这8次射击成绩的方差.（填“变大”、“变小”、“不变”）

    查看试题解析

  • 20. 从2名男生和2名女生中随机抽取上海迪斯尼乐园志愿者.
    (1)、抽取1名，恰好是男生的概率是；
    (2)、抽取2名，用列表法或画树状图法求恰好是1名男生和1名女生的概率.

    查看试题解析

  • 21. 如图，△ABC中，D是BC上一点，∠DAC＝∠B，E为AB上一点.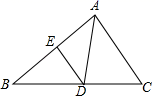

    (1)、求证：△CAD∽△CBA；
    (2)、若BD＝10，DC＝8，求AC的长；

    查看试题解析

  • 22. 已知二次函数y＝ax2＋bx＋c（a≠0），该函数y与自变量x的部分对应值如下表：

    x

    …

    1

    2

    3

    …

    y

    …

    0

    ﹣1

    0

    …
    (1)、求该二次函数的表达式；
    (2)、不等式ax2＋bx＋c＞0的解集为；

    不等式ax2＋bx＋c＜3的解集为.

    查看试题解析

  • 23. 如图，用长6m的铝合金条制成“日”字形窗框，窗框的宽和高各是多少时，窗户的透光面积为1.5m2 (铝合金条的宽度不计) ?

    查看试题解析

  • 24. 如图，⊙O是△ABC的外接圆，∠ABC＝45°，OC∥AD，AD交BC的延长线于D，AB交OC于E.

    (1)、求证：AD是⊙O的切线；
    (2)、若AE＝2 10 ，CE＝4.求图中阴影部分（弦AC和劣弧AC围成的部分）的面积.

    查看试题解析

  • 25. 如图1，在△ABC中，AB=AC=5，BC=6，正方形DEFG的顶点D、G分别在AB、AC上，EF在BC上.

    (1)、求正方形DEFG的边长；
    (2)、如图2，在BC边上放两个小正方形DEFG、FGMN，则DE=.

    查看试题解析

  • 26. 某商店经过市场调查，整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表：

    时间x(天)

    1≤x＜50

    50≤x≤90

    售价(元/件)

    x＋40

    90

    每天销量(件)

    200－2x

    已知该商品的进价为每件30元，设销售该商品的每天利润为y元.

    (1)、求出y与x的函数关系式；
    (2)、问销售该商品第几天时，当天销售利润最大，最大利润是多少？

    查看试题解析

  • 27. 如图，在平面直角坐标系中，抛物线y＝ax2+bx﹣5交y轴于点A，交x轴于点B（﹣5，0）和点C（1，0），过点A作AD∥x轴交抛物线于点D.

    (1)、求此抛物线的表达式；
    (2)、点E是抛物线上一点，且点E关于x轴的对称点在直线AD上，求△EAD的面积；
    (3)、若点P是直线AB下方的抛物线上一动点，当点P运动到某一位置时，四边形OAPB的面积最大，求出此时点P的坐标.

    查看试题解析