福建省泉州市2021届九年级上学期数学期末考试试卷

试卷更新日期：2021-04-27 类型：期末考试

进入出卷网下载

一、单选题

1. 下列x的值能使二次根式 $\sqrt{x - 1}$ 有意义的是（）

A、－2 B、－1 C、0 D、1

查看试题解析
2. 若 $\frac{a}{b} = \frac{3}{2}$ ，则 $\frac{a - b}{a}$ 中的值为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、 $\frac{3}{4}$

查看试题解析
3. 与 $\sqrt{2}$ 是同类二次根式的是（）

A、 $\sqrt{\frac{1}{4}}$ B、 $\sqrt{\frac{1}{2}}$ C、 $\sqrt{4}$ D、 $\sqrt{6}$

查看试题解析
4. “翻开华东师大版数学九年级上册，恰好翻到第50页”，这个事件是（）

A、必然事件 B、随机事件 C、不可能事件 D、确定事件

查看试题解析
5. 用配方法解方程 $x^{2} - 4 x + 2 = 0$ 时，配方结果正确的是（）

A、 ${(x + 2)}^{2} = - 2$ B、 ${(x + 2)}^{2} = 2$ C、 ${(x - 2)}^{2} = 2$ D、 ${(x - 2)}^{2} = - 2$

查看试题解析
6. 若 $△ A B C \sim △ A' B' C'$ ，且面积比为 $4 : 9$ ，则其对应边上的高的比（）

A、 $\frac{16}{81}$ B、 $\frac{4}{9}$ C、 $\frac{2}{3}$ D、 $\frac{1}{3}$

查看试题解析
7. 如图，点G是 $△ A B C$ 的重心，过点G作 $D E / / B C$ ，分别交 $A B$ 、 $A C$ 于点D、E，则 $D G$ 与 $G E$ 的关系为（）

A、 $D G = G E$ B、 $D G > G E$ C、 $D G < G E$ D、 $D G = \frac{2}{3} G E$

查看试题解析
8. 在 $R t △ A B C$ 中， $∠ C = 90 °$ ，则下列选项正确的是（）

A、 $\sin A + \sin B < 1$ B、 $\sin A + \sin B > 1$ C、 $\sin A + \sin B = 1$ D、 $\sin A + \sin B \leq 1$

查看试题解析
9. 我国古代数学著作《九章算术》有题如下：“今有邑方二百步，各中开门.出东门一十五步有木.问出南门几何步而见木？”大意是，今有正方形小城 $A B C D$ 的边长 $B C$ 为200步，如图，各边中点分别开一城门，走出东门E15步处有树Q.问出南门F多少步能见到树Q（即求从点F到点P的距离）？（注：步是古代的计量单位）（）

A、 $366 \frac{2}{3}$ 步 B、 $466 \frac{2}{3}$ 步 C、 $566 \frac{2}{3}$ D、 $666 \frac{2}{3}$ 步

查看试题解析
10. 已知a、b是关于x的一元二次方程 $x^{2} - 6 x - n + 1 = 0$ 的两个根，若a、b、5为等腰三角形的边长，则n的值为（）

A、－4 B、8 C、－4或－8 D、4或－8

查看试题解析

二、填空题

11. 计算： $2 \cos 45 °$ ＝．

查看试题解析
12. 一元二次方程x²﹣16=0的解是．

查看试题解析
13. 某水库大坝，其坡面AB的坡度i=1∶ $\sqrt{3}$ ，则斜坡AB的坡角的度数为°.

查看试题解析
14. 如图，在平面直角坐标系中， $△ A B C$ 与 $△ A_{1} B_{1} C$ 是以点C为位似中心的位似图形，则其相似比为.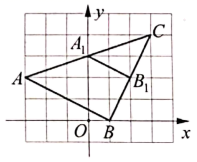

查看试题解析
15. 将一副直角三角尺按如图所示放置， $∠ A = 60 °$ ， $∠ C B D = 45 °$ ， $A C = 2$ ，则 $B D$ 的长为.

查看试题解析
16. 在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C$ ，以 $A C$ 为边作等边三角形 $A C D$ ，直线 $C D$ 与直线 $A B$ 相交于点 $E$ ，则 $\frac{A B}{B E} =$ .

查看试题解析

三、解答题

17. 计算： $\sqrt{8} \times \sqrt{6} - \frac{\sqrt{24}}{\sqrt{2}} + (\sqrt{3} + 1) (\sqrt{3} - 1)$ .

查看试题解析
18. 解方程： $2 x^{2} - 5 x - 2 = 0$

查看试题解析
19. 如图所示，一幅长与宽之比为 $4 ： 1$ 的矩形山水画，欲在其周围镶上一圈宽度为 $1 dm$ 的白纸边框，经测算，镶边后的图画（含白纸边框）的面积为 $504 {dm}^{2}$ ，求原矩形山水面的面积.

查看试题解析
20. 如图是某动车站出口处自动扶梯示意图，自动扶梯 $A B$ 的倾斜角为 $31 °$ ，在自动扶梯下方地面D处测得扶梯顶端A的仰角为 $62 °$ ，B、D之间的距离为 $6 m$ .求自动扶梯的垂直高度 $A C$ .（ $\sin 31 ° \approx 0.52$ ， $\cos 31 ° \approx 0.86$ ， $\tan 31 ° \approx 0.60$ ， $\sin 62 ° \approx 0.88$ ， $\cos 62 ° \approx 0.47$ ， $\tan 62 ° \approx 1.88$ ，结果精确到 $0.1 m$ ）

查看试题解析
21. 如图，A、B、C三点均在边长为1的小正方形网格的格点上.

(1)、请在 $B C$ 上标出点D，连接 $A D$ ，使得 $△ A B D \sim △ C B A$ ；

(2)、试证明上述结论： $△ A B D \sim △ C B A$ .

查看试题解析
22. 已知关于x的一元二次方程 $x^{2} - (m + 2) x + 3 (m - 1) = 0$ .

(1)、请判断这个方程的根的情况，并说明理由；

(2)、若这个方程的一个实根大于1，另一个实根小于0，求m的取值范围.

查看试题解析
23. 在数轴上有一动点M，其平移的方向和距离由以下规则决定：在一个不透明的袋子里装有三个小球，球面上分别标注数字“5”、“－3”、“－3”，它们除数字不同外没有任何区别.试验者先随机摸出一球，记下数字后，将小球放回袋中充分搅匀，再随机摸出一球，并将两球标注的数字之和m作为本次试验的结果.当 $m > 0$ 时，动点M沿数轴正方向平移m个单位；当 $m < 0$ 时，动点M沿数轴负方向平移 $| m |$ 个单位.

(1)、试用画树状图或列表法，求每次试验时动点M平移的方向为数轴正方向的概率；

(2)、若动点M从原点出发，按以上规则连续平移，且以每次平移结束的位置作为下一次平移的起始位置.当试验次数足够多时，请以试验结果m的平均数为依据判断：动点M更可能位于原点的左恻或右侧？并说明理由.

查看试题解析
24. 在平面直角坐标系中，直线 $y = - 2 x + 4$ 与x轴、y轴分别相交于A、B两点，C为 $A B$ 的中点，点D在线段 $O B$ 上（ $B D < O D$ ），连接 $C D$ ，将 $△ B C D$ 绕点C逆时针旋转得到 $△ B' C D'$ ，旋转角为 $α (0 ° < α < 180 °)$ ，连接 $B B'$ ， $B' D$ .

(1)、求 $A B$ 的长；

(2)、如图，当点 $D'$ 恰好落在y轴上时， $B' C$ 交y轴于点E，求证： $△ B E B' \sim △ C E D'$ ；

(3)、当点D的坐标为 $(0 ， 3)$ ，且 $∠ O D B' = ∠ O B A$ 时，求点 $B'$ 的坐标.

查看试题解析
25. 如图，在 $△ A B C$ 中， $A B = 3$ ，点E、D分别是 $A B$ 边上的三等分点， $C D ⊥ A B$ 于点D，点P是 $A C$ 边上的一个动点，连接 $P E$ 、 $E C$ ，作 $△ E P C$ 关于 $A C$ 的轴对称图形 $△ F P C$ .

(1)、当 $P E / / B C$ 时，求 $\frac{A P}{A C}$ 的值；

(2)、当F、P、B三点共线时，求证： $A P \cdot A C = 3$ ；

(3)、当 $C D = 2$ ，且 $A P > P C$ 时，线段 $P E$ 的中垂线 $G Q$ 分别交线段 $P E$ 、 $C D$ 于点G、Q，连接 $P Q$ 、 $E Q$ ，求线段 $P Q$ 的最小值.

查看试题解析