江苏省南通市崇川区2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-04-27 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 某种微生物半径为0.000637米，该数字用科学记数法可表示为（）

A、 $0.637 \times 10^{- 3}$ B、 $6.37 \times 10^{- 4}$ C、 $63.7 \times 10^{- 5}$ D、 $6.37 \times 10^{- 3}$

查看试题解析
3. 下列根式是最简二次根式的是（）

A、 $\sqrt{0.6}$ B、 $\sqrt{\frac{1}{6}}$ C、 $\sqrt{36}$ D、 $\sqrt{26}$

查看试题解析
4. 如图，点B，E，C，F在同一条直线上，已知 $A B = D E$ ， $A C = D F$ ，添加下列条件还不能判定的 $Δ A B C ≅ Δ D E F$ 是（）

A、 $∠ A B C = ∠ D E F$ B、 $∠ A = ∠ D$ C、 $B E = C F$ D、 $B C = E F$

查看试题解析
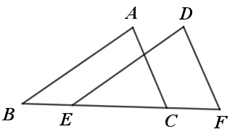5. 在下列运算中，正确的是（）

A、 $a^{3} \cdot a^{4} = a^{12}$ B、 ${(a b^{2})}^{3} = a^{6} b^{6}$ C、 ${(a^{3})}^{4} = a^{7}$ D、 $a^{4} \div a^{3} = a$

查看试题解析
6. 由下列线段a，b，c组成的三角形中，是直角三角形的是（）

A、 $a = 2$ ， $b = 3$ ， $c = 4$ B、 $a = 4$ ， $b = 5$ ， $c = 6$ C、 $a = 5$ ， $b = 12$ ， $c = 13$ D、 $a = 7$ ， $b = 20$ ， $c = 21$

查看试题解析
7. 如图，点D，E分别为 $Δ A B C$ 的边 $A B$ ， $A C$ 上的点，连接 $D E$ 并延长至F，使 $E F = D E$ ，连接 $F C$ .若 $F C / / A B$ ， $A B = 5$ ， $C F = 3$ ，则 $B D$ 的长等于（）

A、 $1$ B、 $2$ C、 $3$ D、 $5$

查看试题解析
8. 如图是由四个全等的直角三角形与一个小正方形拼成的大正方形.若小正方形边长为 $3$ ，大正方形边长为 $15$ ，则一个直角三角形的面积等于（）

A、 $36$ B、 $48$ C、 $54$ D、 $108$

查看试题解析
9. 已知 $x = a$ 时，分式 $\frac{2 x + 1}{x + 1}$ 的值为m.若a取正整数，则m的取值范围为（）

A、 $\frac{1}{2} \leq m < 1$ B、 $1 \leq m < \frac{3}{2}$ C、 $\frac{3}{2} \leq m < 2$ D、 $2 \leq m < \frac{5}{2}$

查看试题解析
10. 如图， $Δ A B C$ 中， $A D ⊥ B C$ ，垂足为D， $A D = B C$ ，P为直线 $B C$ 上方的一个动点， $Δ P B C$ 的面积等于 $Δ A B C$ 的面积的 $\frac{1}{2}$ ，则当 $P B + P C$ 最小时， $∠ P B C$ 的度数为（）

A、 $30 °$ B、 $45 °$ C、 $60 °$ D、 $90 °$

查看试题解析

二、填空题

11. 代数式 $\frac{1}{x - 3}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
12. 已知点A（a，3）与点B（2，b）关于x轴对称，则a+b=.

查看试题解析
13. 分式 $\frac{1}{x^{2} - 4}$ ， $\frac{1}{x + 2}$ 的最简公分母是.

查看试题解析
14. 一个三角形的三条边长分别为 $5$ ， $7$ ，x，另一个三角形的三条边长分别为y， $5$ ， $3$ ，若这两个三角形全等，则 $x + y =$ .

查看试题解析
15. 《九章算术》是中国传统数学的重要著作之一，奠定了中国传统数学的基本框架.如图所示是其中记载的一道“折竹”问题：“今有竹高一丈，末折抵地，去根三尺，问折者高几何？”题意是：一根竹子原高1丈（1丈=10尺），中部有一处折断，竹梢触地面处离竹根3尺，试问折断处离地面多高？答：折断处离地面尺高.

查看试题解析
16. 如图，在长方形 $A B C D$ 内，两个小正方形的面积分别为 $2$ ， $18$ ，则图中阴影部分的面积等于.

查看试题解析
17. 如图， $Δ A B C$ 中， $∠ B = 60 °$ ， $∠ C = 55 °$ ，点D为 $B C$ 边上一动点.分别作点D关于 $A B$ ， $A C$ 的对称点E，F，连接 $A E$ ， $A F$ .则 $∠ E A F$ 的度数等于.

查看试题解析
18. 已知实数m，n满足 $n = k m + 3$ ， $(m^{2} - 2 m + 5) (n^{2} - 4 n + 8) = 16$ ，则 $k =$ .

查看试题解析

三、解答题

19. 计算：

(1)、 ${(- 3)}^{0} - {(\frac{1}{3})}^{- 2} + {(\sqrt{5})}^{2}$ ；

(2)、 $\sqrt{48} \div \sqrt{3} - \sqrt{\frac{1}{2}} \times \sqrt{12} + \sqrt{24}$ .

查看试题解析
20. 先化简，再求值：

(1)、 $[{(2 a - b)}^{2} - (2 a + b) (2 a - b)] \div 2 b$ ，其中 $a = \frac{1}{2}$ ， $b = - 1$ ；

(2)、 $(\frac{3}{a + 1} - a + 1) \div \frac{a^{2} - 4}{a^{2} + 2 a + 1}$ ，其中 $a = - 3$ .

查看试题解析
21. 如图， $A B = A D$ ， $∠ B = ∠ D$ ， $∠ B A D = ∠ C A E = 60 °$ .

(1)、求证： $Δ A B C ≅ Δ A D E$ ；

(2)、若 $A E = 5$ ，求 $C E$ 的长.

查看试题解析
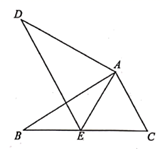22. 如图是由边长为 $1$ 的小正方形构成的网格，每个小正方形的顶点叫做格点.点A，B，C都是格点.

(1)、求证： $A C ⊥ B C$ .

(2)、 $Δ A B C$ 的面积等于

查看试题解析
23. 疫情防控形势下，人们在外出时都应戴上口罩以保护自己免受新型冠状病毒感染.某药店用4000元购进若干包一次性医用口罩，很快售完，该店又用7500元钱购进第二批这种口罩，所进的包数比第一批多50%，每包口罩的进价比第一批每包口罩的进价多0.5元，求购进的第一批医用口罩有多少包？

查看试题解析
24. 如图， $∠ A B C = ∠ D C B = 72 °$ ， $∠ A B C$ ， $∠ D C B$ 的角平分线 $B D$ ， $C A$ 相交于点 $O$ .

(1)、求证： $Δ A O B ≅ Δ D O C$ ；

(2)、我们知道，在直角三角形中， $30 °$ 的角所对的直角边与斜边的比值等于 $\frac{1}{2}$ .类似的，在顶角为 $36 °$ 的等腰三角形中， $72 °$ 的角所对的边与底边的比值等于 $\frac{\sqrt{5} + 1}{2}$ .根据这一结论，若 $A O = 2 \sqrt{5}$ ，求 $Δ A B C$ 的周长.

查看试题解析
25. 如图， $Δ A B C$ 中， $∠ C = 90 °$ ， $A B = 10 c m$ ， $B C = 6 c m$ ，点P从点A出发，在 $Δ A B C$ 的边上以 $2 c m /$ 秒的速度沿 $A \to C \to B \to A$ 运动一周，设运动时间为 $t (t > 0)$ 秒.

(1)、如图1，点P运动到 $B C$ 边上，且 $A P$ 恰好平分 $∠ B A C$ ，求t的值；

(2)、在点P运动过程中，当 $Δ C B P$ 是以 $C B$ 为腰的等腰三角形时，求t的值.

查看试题解析
26. 定义：三角形中，连接一个顶点和它所对的边上一点，如果所得线段把三角形的周长分成相等的两部分，则称这条线段为三角形的“周长平分线”.

(1)、下列与等腰三角形相关的线段中，一定是所在等腰三角形的“周长平分线”的是（只要填序号）；
①腰上的高；②底边上的中线；③底角平分线.

(2)、如图1，在四边形 $A B C D$ 中， $∠ B = ∠ C = 45 °$ ，P为 $B C$ 的中点， $∠ A P D = 90 °$ .取 $A D$ 中点Q，连接 $P Q$ .求证： $P Q$ 是 $Δ A P D$ 的“周长平分线”.

(3)、在（2）的基础上，分别取 $A P$ ， $D P$ 的中点M，N，如图2.请在 $B C$ 上找点E，F，使 $E M$ 为 $Δ A P E$ 的“周长平分线”， $F N$ 为 $Δ D P F$ 的“周长平分线”.
①用无刻度直尺确定点E，F的位置（保留画图痕迹）；

②若 $A B = \sqrt{2}$ ， $C D = 2 \sqrt{2}$ ，直接写出 $E F$ 的长.

查看试题解析