湖北省孝感市2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-04-27 类型:期末考试
一、单选题
-
1. 如图甲骨文中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各组线段,能构成三角形的是( )A、 B、 C、 D、3. 下列式子正确的是( )A、 B、 C、 D、4. 若分式 ,则 的值为( )A、 B、 C、 D、5. 已知点 与点 关于x轴对称,那么 的值为( )A、1 B、 C、7 D、6. 下列各式从左到右的变形中,是因式分解的为( )A、 B、 C、 D、7. 用直尺和圆规画一个角等于已知角,是运用了“全等三角形的对应角相等”这一性质,其全等的依据是( )
2. 下列各组线段,能构成三角形的是( )A、 B、 C、 D、3. 下列式子正确的是( )A、 B、 C、 D、4. 若分式 ,则 的值为( )A、 B、 C、 D、5. 已知点 与点 关于x轴对称,那么 的值为( )A、1 B、 C、7 D、6. 下列各式从左到右的变形中,是因式分解的为( )A、 B、 C、 D、7. 用直尺和圆规画一个角等于已知角,是运用了“全等三角形的对应角相等”这一性质,其全等的依据是( )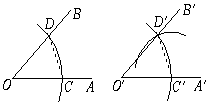 A、SAS B、ASA C、AAS D、SSS8. 如图, 为 平分线 上一点, , 的面积为12,则点 到直线 的距离为( )
A、SAS B、ASA C、AAS D、SSS8. 如图, 为 平分线 上一点, , 的面积为12,则点 到直线 的距离为( )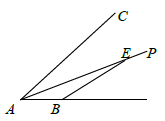 A、3 B、4 C、5 D、69. 如图,已知Rt△OAB,∠OAB=50°,∠AOB=90°,O点与坐标系原点重合,若点P在x轴上,且△APB是等腰三角形,则点P的坐标可能有( ).
A、3 B、4 C、5 D、69. 如图,已知Rt△OAB,∠OAB=50°,∠AOB=90°,O点与坐标系原点重合,若点P在x轴上,且△APB是等腰三角形,则点P的坐标可能有( ).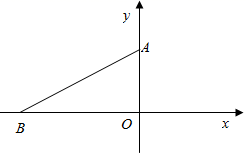 A、1个 B、2个 C、3个 D、4个10. 如图, 中, 的平分线 与边 的垂直平分线 相交于 交 的延长线于 于F,现有下列结论:① ;② ;③ 平分 ;④若 ,则 .其中正确的个数为( )
A、1个 B、2个 C、3个 D、4个10. 如图, 中, 的平分线 与边 的垂直平分线 相交于 交 的延长线于 于F,现有下列结论:① ;② ;③ 平分 ;④若 ,则 .其中正确的个数为( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 科学家测得新冠病毒的直径为 ,用科学记数法表示为.12. 若 是完全平方公式,则 .13. 若一个多边形的内角和与外角和之和是900°,则该多边形的边数是 .14. 如图, ,要使 ,还需添加一个条件是:.(填上你认为适当的一个条件即可)
 15. 若 ,则 .16. 如图,在锐角 中, ,边 上有一定点 分别是 和 边上的动点,当 的周长最小时, 的度数是.
15. 若 ,则 .16. 如图,在锐角 中, ,边 上有一定点 分别是 和 边上的动点,当 的周长最小时, 的度数是.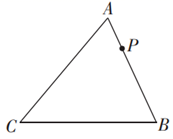
三、解答题
-
17.(1)、计算:(2)、分解因式:18. 解方程:19. 先化简,再求值:(m﹣ )× ,其中m=﹣1.20. 如图,在平面直角坐标系中,△ABC三个顶点的坐标为A(1,2),B(4,1),C(2,4).

( 1 )在图中画出△ABC关于y轴对称的图形△A′B′C′;
( 2 )在图中x轴上作出一点P,使PA+PB的值最小;并写出点P的坐标.
21. 如图,∠A=∠D=90°,AB=DC,点E,F在BC上且BE=CF.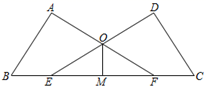 (1)、求证:AF=DE;(2)、若OM平分∠EOF,求证:OM⊥EF.22. 新型冠状病毒肺炎疫情发生后,全社会积极参与疫情防控.甲、乙两个工厂生产同一种防护口罩,甲厂每天比乙厂多生产口罩5万只,甲厂生产该种口罩40万只所用时间与乙厂生产该种口罩15万只所用时间相同.(1)、求甲、乙两个工厂每天分别生产该种口罩多少万只?(2)、甲、乙两厂接到一笔订单,要求10日内生产200万只该种口罩,乙厂引进设备提升产能,为完成订单,乙厂至少每天要多生产多少万只该种口罩?23. 问题背景:
(1)、求证:AF=DE;(2)、若OM平分∠EOF,求证:OM⊥EF.22. 新型冠状病毒肺炎疫情发生后,全社会积极参与疫情防控.甲、乙两个工厂生产同一种防护口罩,甲厂每天比乙厂多生产口罩5万只,甲厂生产该种口罩40万只所用时间与乙厂生产该种口罩15万只所用时间相同.(1)、求甲、乙两个工厂每天分别生产该种口罩多少万只?(2)、甲、乙两厂接到一笔订单,要求10日内生产200万只该种口罩,乙厂引进设备提升产能,为完成订单,乙厂至少每天要多生产多少万只该种口罩?23. 问题背景:我们学习等边三角形时得到直角三角形的一个性质:在直角三角形中,如果一个锐角等于 ,那么它所对的直角边等于斜边的一半,即如图甲,在 中, , ,则 .
探究结论:
小明同学对以上结论作了进一步探究.
 (1)、如图甲,作 边上的中线 ,得到结论: 为等边三角形,请加以证明;(2)、如图乙, 是 的中线,点D是边 上任意一点,连接 ,作等边 ,且点P在 的内部,连接 ,求证:
(1)、如图甲,作 边上的中线 ,得到结论: 为等边三角形,请加以证明;(2)、如图乙, 是 的中线,点D是边 上任意一点,连接 ,作等边 ,且点P在 的内部,连接 ,求证:①
② .
24. 如图,在平面直角坐标系中, 两点的坐标分别是点 ,点 ,且 满足: . (1)、求 的度数;(2)、点D是y轴正半轴上A点上方一点(不与A点重合),以 为腰作等腰 ,过点C作 轴于点E.
(1)、求 的度数;(2)、点D是y轴正半轴上A点上方一点(不与A点重合),以 为腰作等腰 ,过点C作 轴于点E.①求证: ;
②连接 交x轴于点F,若 ,求点F的坐标.