广西壮族自治区河池市宜州区2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-04-27 类型：期末考试

进入出卷网下载

一、单选题

1. 计算 ${(- 2020 - 1)}^{0}$ 的结果是（）

A、-2019 B、2019 C、-2021 D、1

查看试题解析
2. 下列银行标志中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 若 $a + b = 2$ ， $a - b = 6$ ，则 $b^{2} - a^{2}$ 的值是（）

A、-12 B、12 C、8 D、-8

查看试题解析
4. 2020年6月23日，我国成功发射了北斗系统第55颗导航卫星，其授时精度为世界之最，不超过0.0000000099秒.将数据“0.0000000099”用科学记数法表示为（　　）

A、 $99 \times 10^{- 10}$ B、 $9.9 \times 10^{- 10}$ C、 $9.9 \times 10^{- 9}$ D、 $9.9 \times 10^{- 8}$

查看试题解析
5. 下列运算正确的是（）

A、 $(4 x^{3} - 2 x^{2}) \div 2 x = 2 x^{2} - 1$ B、 $x^{3} x^{2} = x^{6}$ C、 $x^{2} y^{3} \div (x y^{3}) = x$ D、 ${(x^{2} y^{3})}^{2} = x^{4} y^{5}$

查看试题解析
6. 多项式 $a x^{2} - 4 a$ 与多项式 $x^{2} + 4 x + 4$ 的公因式是（）

A、 $x + 2$ B、 $x - 2$ C、 $x^{2} - 2$ D、 ${(x - 2)}^{2}$

查看试题解析
7. 如果分式 $\frac{3}{x - 3}$ 有意义，则x的取值范围是（）

A、 $x > 3$ B、 $x \neq 3$ C、 $x < 3$ D、 $x \neq - 3$

查看试题解析
8. 若等腰三角形的周长是 $22 cm$ ，其中一边长为 $10 cm$ ，则腰长是（　　）

A、 $10 cm$ B、 $6 cm$ C、 $6 cm$ 或 $10 cm$ D、无法确定

查看试题解析
9. 已知一个n边形的每一个外角都相等，一个内角与其相邻的一个外角的度数之比是 $7 : 2$ ，则n的值是（）

A、8 B、9 C、10 D、12

查看试题解析
10. 如图，在 $△ A B C$ 中， $A B = B C$ ， $D E$ 垂直平分 $B C$ ，若 $∠ B = 40 °$ ，则 $∠ A C D$ 的度数等于（）

A、 $50 °$ B、 $40 °$ C、 $30 °$ D、 $20 °$

查看试题解析
11. 如图，乐乐书上的三角形墨迹污染了一部分，很快他就画出一个三角形与书上的三角形全等，这两个三角形全等的依据是（）

A、 $S S S$ B、 $A S A$ C、 $A A S$ D、 $S A S$

查看试题解析
12. 如图， $△ A B C$ 和 $△ A D E$ 都是等边三角形， $A D$ 是 $△ A B C$ 的角平分线，下列结论：① $A D ⊥ B C$ ；② $A F ⊥ D E$ ；③ $B E = B D$ ；④ $B C = D E$ ，其中结论正确的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

13. 如果 $2^{x} = 3$ ， $2^{y} = 7$ ，则 $2^{x + y} =$ .

查看试题解析
14. 已知 $△ A B C$ 的三边长为2，7， $x$ ，请写出一个符合条件的 $x$ 的整数值，这个值可以是.

查看试题解析
15. 若点 $A (2, m)$ 与点 $B (2, - 3)$ 关于x轴对称，则 $m =$ .

查看试题解析
16. 若方程 $\frac{x - 1}{x - 5} = \frac{2 m}{x - 5}$ 无解，则 $m =$ .

查看试题解析
17. 如图，在平面直角坐标系中，已知 $A (2 ， 0)$ ， $B (0 ， 3)$ ，若在第一象限中找一点C，使得 $△ A O C ≅ △ O A B$ ，则C点的坐标为.

查看试题解析
18. 如图，在等腰直角 $△ A B C$ 中， $∠ A C B = 90 °$ ，O是斜边 $A B$ 的中点，点D，E分别在直角边 $A C$ ， $B C$ 上，且 $∠ D O E = 90 °$ ，若 $A C = 3$ ，则 $A D + B E =$ .

查看试题解析

三、解答题

19. 因式分解： $- a x^{2} - a y^{2} - 2 a x y$ .

查看试题解析
20. 当x为何值时， $x^{- 1}$ 与 $5 {(x + 3)}^{- 1}$ 的值相等.

查看试题解析
21. 化简求值： $(\frac{x^{2}}{x - 2} - \frac{3 x}{2 - x}) \div \frac{x}{x - 2}$ ，其中 $x = - 4$ .

查看试题解析
22. 如图所示，在 $△ A B C$ 中， $A B = A C$ .

(1)、尺规作图：过点A作 $△ A B C$ 的角平分线 $A D$ （不写作法，保留作图痕迹）；

(2)、在 $A D$ 上任取一点E，连接 $B E$ 、 $C E$ .求证： $∠ A B E = ∠ A C E$ .

查看试题解析
23. 如图，已知， $∠ B = ∠ E$ ， $B C = D E$ ， $A B = A E$ .

求证： $∠ 1 = ∠ 2$ .

查看试题解析
24. 如图，已知 $△ A D F ≅ △ C B E$ ，点B、D在线段 $E F$ 上.

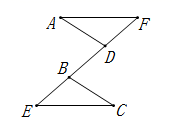(1)、线段 $A D$ 与 $B C$ 的数量关系是：，判断该关系的数学根据是：（用文字表达）；

(2)、判断 $A D$ 与 $B C$ 之间的位置关系，并说明理由.

查看试题解析
25. 为响应国务院大力发展“地摊经济”的号召，某地政府拟建甲，乙两类摊位供市民开展“地摊”创业，每个甲类摊位的占地面积比每个乙类摊位的占地面积多 $2 m^{2}$ .建甲类摊位的费用为50元 $/ m^{2}$ ，建乙类摊位的费用为40元 $/ m^{2}$ .用 $60 m^{2}$ 建甲类摊位的个数恰好是用同样面积建乙类摊位个数的 $\frac{2}{3}$ .

(1)、求每个甲，乙类摊位占地面积各多少 $m^{2}$ ？

(2)、相关部门在某路段规划了两块均为 $240 m^{2}$ 的场地分别用于建设甲，乙类摊位，则建好这些摊位，政府投入的资金共计多少元.

查看试题解析
26. 如图，在平面直角坐标系中， $△ A O B$ 为等边三角形，点 $A (0 ， 2)$ 上方的C为y轴上一动点，以 $B C$ 为边作等边 $△ B C D$ ，直线 $A D$ 交x轴于点E.

(1)、当点C运动到 $(0 ， 3)$ 时， $A D =$ ；

(2)、猜想 $∠ D A B =$ 度，并说明理由；

(3)、当点C运动时， $A E$ 的长度是否发生变化？若不变，求出 $A E$ 的值；若变化，请说明理由.

查看试题解析