福建省三明市永安市2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-04-27 类型：期末考试

进入出卷网下载

一、单选题

1. $△ A B C$ 中， $∠ A$ 、 $∠ B$ 、 $∠ C$ 的对边分别为a、b、c，若 $a^{2} = b^{2} + c^{2}$ ，则有（）

A、 $∠ A = 90 °$ B、 $∠ B = 90 °$ C、 $∠ C = 90 °$ D、 $∠ C = ∠ A + ∠ B$

查看试题解析
2. 下列说法中正确的是（）．

A、0.09的平方根是0.3 B、 $\sqrt{16} = \pm 4$ C、0的立方根是0 D、1的立方根是 $\pm 1$

查看试题解析
3. 已知点M（3，﹣2），N（3，﹣1），则线段MN与x轴（　　）

A、垂直 B、平行 C、相交 D、不垂直

查看试题解析
4. 若 $m < 2 \sqrt{7} < m + 1$ ，且m为整数，则m的值为（）.

A、3 B、4 C、5 D、6

查看试题解析
5. 下列运算，结果正确的是（）

A、 $\sqrt{5} - \sqrt{3} = \sqrt{2}$ B、 $3 + \sqrt{2} = 3 \sqrt{2}$ C、 $\sqrt{6} \div \sqrt{2} = 3$ D、 $\sqrt{6} \times \sqrt{2} = 2 \sqrt{3}$

查看试题解析
6. 在一次青年歌手比赛中，七位评委为某位歌手打出的分数如下：9.5，9.4，9.6，9.9，9.3，9.7，9.0（单位：分）．若去掉一个最高分和一个最低分，则去掉前与去掉后没有改变的一个统计量是（）

A、平均分 B、方差 C、中位数 D、极差

查看试题解析
7. 《九章算术》是中国古代第一部数学专著，它对我国古代后世的数学家产生了深远的影响，该书中记载了一个问题，大意是：有几个人一起去买一件物品，每人出8元，多3元；每人出7元，少4元，问有多少人？该物品价几何？设有x人，物品价值y元，则所列方程组正确的是（）

A、 ${\begin{matrix} 8 y + 3 = x \\ 7 y - 4 = x \end{matrix}$ B、 ${\begin{matrix} 8 x + 3 = y \\ 7 x - 4 = y \end{matrix}$ C、 ${\begin{matrix} 8 x - 3 = y \\ 7 x + 4 = y \end{matrix}$ D、 ${\begin{matrix} 8 y - 3 = x \\ 7 y + 4 = x \end{matrix}$

查看试题解析
8. 如图，直线 a⊥b ，在某平面直角坐标系中，x轴 $// a$ ，y轴 $// b$ ，点A的坐标为 $(- 3 ， 2)$ ，点B的坐标为 $(2 ， - 3)$ ，则坐标原点为（）

A、 $O_{1}$ B、 $O_{2}$ C、 $O_{3}$ D、 $O_{4}$

查看试题解析
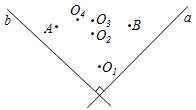9. 一组数据2，0，1，4，3，这组数据的方差是（）

A、2 B、4 C、1 D、3

查看试题解析
10. 当k取不同的值时，y关于x的函数y=kx+2（k≠0）的图象为总是经过点（0，2）的直线，我们把所有这样的直线合起来，称为经过点（0，2）的“直线束”.那么，下面经过点（﹣1，2）的直线束的函数式是（　　）

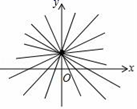A、y=kx﹣2（k≠0） B、y=kx+k+2（k≠0） C、y=kx﹣k+2（k≠0） D、y=kx+k﹣2（k≠0）

查看试题解析

二、填空题

11. 计算： $\sqrt[3]{- 8}$ = ．

查看试题解析
12. 把命题“对顶角相等”改写成“如果…那么…”的形式是.

查看试题解析
13. 将一个含 $45^{\circ}$ 的三角尺和一把直尺按如图所示摆放，若 $∠ 1 = 20 °$ ，则 $∠ 2 =$ $^{\circ}$ ．

查看试题解析
14. 在如图的方格中，若要使横，竖，斜对角的3个实数相乘都得到同样的结果，则图中m的值为.

$3 \sqrt{2}$

2

$\sqrt{3}$

1

m

6

3

$\sqrt{2}$

查看试题解析
15. 已知一次函数 $y = 2 x - 1$ 的图象经过 $A (x_{1} ， 1)$ ， $B (x_{2} ， 3)$ 两点，则 $x_{1}$ $x_{2}$ （填“ $>$ ”“ $<$ ”或“ $=$ ”）.

查看试题解析
16.
如图1，点P从△ABC的顶点B出发，沿B→C→A匀速运动到点A，图2是点P运动时，线段BP的长度y随时间x变化的关系图象，其中M为曲线部分的最低点，则△ABC的面积是．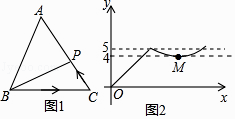

查看试题解析

三、解答题

17. 计算∶

(1)、 $\sqrt{\frac{1}{7}} - \sqrt{28}$

(2)、 ${(1 - \sqrt{3})}^{2} - | \sqrt{3} - 2 |$

查看试题解析
18. 如图，在 $4 \times 4$ 的正方形网格中，每个小格的顶点叫做格点，以格点为顶点分别按下列要求画三角形.

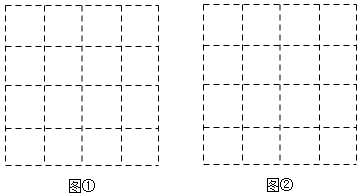(1)、在图①中，画一个直角三角形，使它的三边长都是有理数；

(2)、在图②中，画一个直角三角形，使它的三边长都是无理数.

查看试题解析
19. 在如图所示的正方形网格中，每个小正方形的边长为1， $△ A B C$ 的顶点均在小正方形的顶点上.

（ 1 ）在图中建立恰当的平面直角坐标系，且使点C的坐标为 $(- 1 ， 3)$ ；

（ 2 ）在（1）中建立的平面直角坐标系内画出 $△ A B C$ 关于y轴对称的 $△ A_{1} B_{1} C_{1}$ ；

（ 3 ）点 $B_{1}$ 的坐标为_▲_。

查看试题解析
20. 如图，直线 $l_{1}$ ： $y = x + 3$ 与过点 $A (3 ， 0)$ 的直线 $l_{2}$ 交于点 $C (1 ， m)$ .

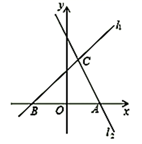(1)、求m的值；

(2)、求直线 $l_{2}$ 的解析式.

查看试题解析
21. 某天，一蔬菜经营户从蔬菜批发市场批发了黄瓜和茄子共120千克，到菜市场去卖，黄瓜和茄子当天的批发价和零售价如下表所示∶

品名

黄瓜

茄子

批发价/（元/千克）

2.4

2.2

零售价/（元/千克）

3.6

3

(1)、若他当天批发两种蔬菜共花去280元，则购进黄瓜和茄子各多少千克？

(2)、他当天卖完这些黄瓜和茄子可赚多少元？

查看试题解析

22. 小江带领村民利用微商平台，在线推广和销售本地特产柑桔.通过一个月的努力跟进，柑桔的销售有了很大的起色，为了了解这个月每户村民的柑桔销售情况，小江随机从A、B两村各抽取20户村民的“柑桔”销量

x

（单位∶箱）进行调查，并得到如下统计图表∶

B村柑桔销量统计表

x（单位：箱）	$x < 40$	$40 \leq x < 50$	$50 \leq x < 60$	$x \geq 60$
B村村民户数	a	6	5	b

小江在统计中发现，销量低于50箱的具体情况如下∶

A村∶33，40，27，34，49，42，16，48，42，43，48，38

B村∶9，22，40，43，35，48，45，47，30，33，39，30，45

根据上述信息回答下列问题∶

(1)、填空∶

a =

，

b =

(2)、根据调查数据完成了表中的统计量∶则

m =

村名	平均数	中位数	众数
A村	48.8	m	59
B村	47.4	45	56

(3)、你认为A、B两村中哪个村的柑桔卖得更好？请说明理由.

查看试题解析

23. 如图，已知∠1+∠2＝180°，∠3＝B，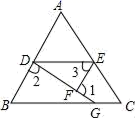

(1)、证明：EF∥AB.

(2)、试判断∠AED与∠C的大小关系，并说明你的理由.

查看试题解析
24. 有些关于方程组的问题，欲求的结果不是每一个未知数的值，而是关于未知数的代数式的值，如以下问题∶
已知实数x、y满足 $3 x - y = 5$ ①， $2 x + 3 y = 7$ ②，求 $x - 4 y$ 和 $7 x + 5 y$ 的值.

本题常规思路是将①②两式联立组成方程组，解得x、y的值再代入欲求值的代数式得到答案，常规思路运算量比较大.其实，仔细观察两个方程未知数的系数之间的关系，本题还可以通过适当变形整体求得代数式的值，如由① $-$ ②可得 $x - 4 y = - 2$ ，由①＋② $\times 2$ 可得 $7 x + 5 y = 19$ .这样的解题思想就是通常所说的“整体思想”.解决问题∶

(1)、已知二元一次方程组 ${\begin{array}{l} 3 x + 2 y = 7 \\ 2 x + 3 y = 3 \end{array}$ 则 $x - y =$ ， $x + y =$ .

(2)、某班级组织活动购买小奖品，买13支铅笔、5块橡皮、2本日记本共需31元，买25支铅笔、9块橡皮、3本日记本共需55元，则购买3支铅笔、3块橡皮、3本日记本共需多少元？

(3)、对于实数x、y，定义新运算∶ $x * y = a x + b + c$ ，其中a、b、c是常数，等式右边是通常的加法和乘法运算.已知 $3 * 5 = 16$ ， $2 * 3 = 12$ ，那么 $5 * 9 =$ .

查看试题解析
25. 已知，在 $△ A B C$ 中，点E在边 $A B$ 上，点D是 $B C$ 上一个动点，将 $∠ B$ 沿E、D所在直线进行翻折得到 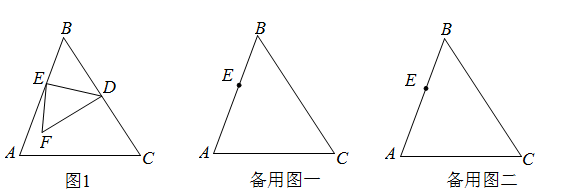$∠ E F D$ ，

(1)、如图1，若 $∠ B = 50 °$ ，则 $∠ A E F + ∠ F D C =$ ；

(2)、在图1中细心的小明发现了 $∠ A E F$ ， $∠ F D C$ ， $∠ B$ 之间的关系，请您替小明写出这个数量关系并证明；

(3)、小明进一步探索发现∶当 $B D =$ _▲_时，有 $E F // B D$ ，请你证明这个结论；

(4)、若点D在线段 $B C$ 上运动，问小明发现的 $∠ A E F$ ， $∠ F D C$ ， $∠ B$ 的数量关系会变吗？请你在备用图中画出一个不同于图1的示意图，并直接写出你的结论.

查看试题解析

品名	黄瓜	茄子
批发价/（元/千克）	2.4	2.2
零售价/（元/千克）	3.6	3

$3 \sqrt{2}$	2	$\sqrt{3}$
1	m	6
	3	$\sqrt{2}$