湘教版备考2021年中考数学二轮复习专题10三角形
试卷更新日期:2021-04-26 类型:二轮复习
一、单选题
-
1. 如图,在锐角 中, , , 是 内的两点, 平分 , ,若 , ,则 的长度是( )
 A、 B、 C、 D、2. 如图,已知直线AB:y= 分别交x轴、y轴于点B、A两点,C(3,0),D、E分别为线段AO和线段AC上一动点,BE交y轴于点H,且AD=CE.当BD+BE的值最小时,则H点的坐标为( )
A、 B、 C、 D、2. 如图,已知直线AB:y= 分别交x轴、y轴于点B、A两点,C(3,0),D、E分别为线段AO和线段AC上一动点,BE交y轴于点H,且AD=CE.当BD+BE的值最小时,则H点的坐标为( ) A、 B、(0,5) C、(0,4) D、3. 如图,C为线段BE上一动点 不与点B,E重合 ,在BE同侧分别作等边ABC和等边CDE、BD与AE交于点P,BD与AC交于点M,AE与CD交于点N,连结MN.以下四个结论:①CM=CN;②∠APB=60°;③PA+PC=PB;④PC平分∠BPE;恒成立的结论有( )
A、 B、(0,5) C、(0,4) D、3. 如图,C为线段BE上一动点 不与点B,E重合 ,在BE同侧分别作等边ABC和等边CDE、BD与AE交于点P,BD与AC交于点M,AE与CD交于点N,连结MN.以下四个结论:①CM=CN;②∠APB=60°;③PA+PC=PB;④PC平分∠BPE;恒成立的结论有( )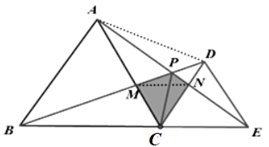 A、①②④ B、①②③④ C、①③④ D、①④4. 如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC、FG,则下列结论要:①AE= BD;②AG= BF ;③FG∥BE;④OC平分∠BOE,其中结论正确的个数有( )
A、①②④ B、①②③④ C、①③④ D、①④4. 如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC、FG,则下列结论要:①AE= BD;②AG= BF ;③FG∥BE;④OC平分∠BOE,其中结论正确的个数有( )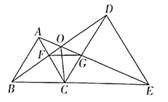 A、1个 B、2个 C、3个 D、4个5. 在 中, , ,点 是边 上一定点,此时分别在边 , 上存在点 , 使得 周长最小且为等腰三角形,则此时 的值为( )
A、1个 B、2个 C、3个 D、4个5. 在 中, , ,点 是边 上一定点,此时分别在边 , 上存在点 , 使得 周长最小且为等腰三角形,则此时 的值为( ) A、1 B、2 C、3 D、6. 如图所示,已知在Rt△ABC中,∠C = 90°,AC = 4,BC = 3,以△ABC的一条边为边画等腰三角形,使它的第三个顶点在△ABC的其他边上,则这样的点有( )
A、1 B、2 C、3 D、6. 如图所示,已知在Rt△ABC中,∠C = 90°,AC = 4,BC = 3,以△ABC的一条边为边画等腰三角形,使它的第三个顶点在△ABC的其他边上,则这样的点有( ) A、7个 B、6个 C、5个 D、4个7. 如图,已知∠A=10°,在∠A两边上分别作点,并连接这些点,使 AB=BC=CD=DE……一直作下去,那么图中以这些线段为腰长的等腰三角形最多能找到( )
A、7个 B、6个 C、5个 D、4个7. 如图,已知∠A=10°,在∠A两边上分别作点,并连接这些点,使 AB=BC=CD=DE……一直作下去,那么图中以这些线段为腰长的等腰三角形最多能找到( ) A、7个 B、8个 C、9个 D、10个8. 如图,在等边△ABC中,AD⊥BC于D,延长BC到E,使CE= BC,F是AC的中点,连接EF并延长EF交AB于G,BG的垂直平分线分别交BG,AD于点M,点N,连接GN,CN,下列结论:①EG∥MN;②GF= EF;③∠GNC=120°.其中正确的是( )
A、7个 B、8个 C、9个 D、10个8. 如图,在等边△ABC中,AD⊥BC于D,延长BC到E,使CE= BC,F是AC的中点,连接EF并延长EF交AB于G,BG的垂直平分线分别交BG,AD于点M,点N,连接GN,CN,下列结论:①EG∥MN;②GF= EF;③∠GNC=120°.其中正确的是( ) A、①② B、①③ C、②③ D、①②③9. 如图, ,点 、 、 …在射线 上,点 、 、 …在射线 上, 、 、 …均为等边三角形,依此类推,若 ,则 的边长为( )
A、①② B、①③ C、②③ D、①②③9. 如图, ,点 、 、 …在射线 上,点 、 、 …在射线 上, 、 、 …均为等边三角形,依此类推,若 ,则 的边长为( ) A、 B、 C、2016 D、403210. 如图,已知△ABC和△DCE均是等边三角形,点 B、C、E 在同一条直线上,AE与 BD交于点 O,AE与 CD交于点 G,AC与 BD交于点 F,连接 OC、FG,则下列结论要:①AE=BD;②AG=BF;③FG∥BE;④OC 平分∠BOE,其中结论正确的个数有( )
A、 B、 C、2016 D、403210. 如图,已知△ABC和△DCE均是等边三角形,点 B、C、E 在同一条直线上,AE与 BD交于点 O,AE与 CD交于点 G,AC与 BD交于点 F,连接 OC、FG,则下列结论要:①AE=BD;②AG=BF;③FG∥BE;④OC 平分∠BOE,其中结论正确的个数有( )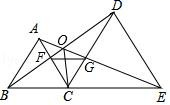 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 如图,在四边形 中, 于点 ,且 平分 ,若 的面积为 ,则 的面积为 .
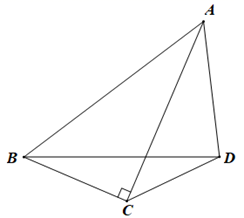 12. 如图,△ABC中(AB>BC),G在CB的延长线上,边AC的垂直平分线DE与∠ABG的角平分线交于点M,与AB交于点D,与AC相交于E,MN⊥AB于N.已知AB=13,BC=9,MN=3,则△BMN的面积是.
12. 如图,△ABC中(AB>BC),G在CB的延长线上,边AC的垂直平分线DE与∠ABG的角平分线交于点M,与AB交于点D,与AC相交于E,MN⊥AB于N.已知AB=13,BC=9,MN=3,则△BMN的面积是. 13. 如图,在第一个△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2 , 使得A1A2=A1C,得到第二个△A1A2C;在A2C上取一点D,延长A1A2=A2D;…,按此做法进行下去,则第5个三角形中,以点A4为顶点的等腰三角形的底角的度数为.
13. 如图,在第一个△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2 , 使得A1A2=A1C,得到第二个△A1A2C;在A2C上取一点D,延长A1A2=A2D;…,按此做法进行下去,则第5个三角形中,以点A4为顶点的等腰三角形的底角的度数为. 14. 如图,△ABC是边长6cm的等边三角形,动点P、Q同时从A、B两点出发,分别在AB、BC边上均速移动,它们的速度分别为Vp=2cm/s,Vq=1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为ts,则当t= s时,△PBQ为直角三角形。
14. 如图,△ABC是边长6cm的等边三角形,动点P、Q同时从A、B两点出发,分别在AB、BC边上均速移动,它们的速度分别为Vp=2cm/s,Vq=1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为ts,则当t= s时,△PBQ为直角三角形。 15. 已知点A,B的坐标分别为(2,0),(2,4),以A,B,P为顶点的三角形与 全等,点P与点O不重合,写出符合条件的点P的坐标: .16. 如图,在△ABC中,∠ACB=90º,∠BAC=30º,在直线BC或AC上取一点P,使得△PAB为等腰三角形,则符合条件的点P共有个.
15. 已知点A,B的坐标分别为(2,0),(2,4),以A,B,P为顶点的三角形与 全等,点P与点O不重合,写出符合条件的点P的坐标: .16. 如图,在△ABC中,∠ACB=90º,∠BAC=30º,在直线BC或AC上取一点P,使得△PAB为等腰三角形,则符合条件的点P共有个.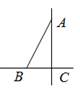 17. 如图, 与 中,AB=AE , BC=EF , ∠B=∠E , AB交EF于D . 给出下列结论:①∠AFC=∠C;②DF=CF;③FA是∠DFC的平分线;④∠BFD=∠CAF . 其中正确的结论是:(填写所有正确结论的序号).
17. 如图, 与 中,AB=AE , BC=EF , ∠B=∠E , AB交EF于D . 给出下列结论:①∠AFC=∠C;②DF=CF;③FA是∠DFC的平分线;④∠BFD=∠CAF . 其中正确的结论是:(填写所有正确结论的序号). 18. 如图,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的角平分线,CA2是∠A1CD的角平分线,BA3是∠A2BD的角平分线,CA3是∠A2CD的角平分线,若∠A=64°,则∠A= , ∠A3= , 若∠A=α,则∠A2018为。
18. 如图,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的角平分线,CA2是∠A1CD的角平分线,BA3是∠A2BD的角平分线,CA3是∠A2CD的角平分线,若∠A=64°,则∠A= , ∠A3= , 若∠A=α,则∠A2018为。 19. 如图,在△ABC中,AB=AC=24厘米,∠B=∠C ,BC=16厘米,点D为AB的中点,点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为厘米/秒时,能够在某一时刻使△BPD与△CQP全等.
19. 如图,在△ABC中,AB=AC=24厘米,∠B=∠C ,BC=16厘米,点D为AB的中点,点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为厘米/秒时,能够在某一时刻使△BPD与△CQP全等.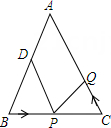 20. 如图,已知直线 : ,过点 作直线 的垂线交 轴于点 ,过点 作 轴的垂线交直线 于点 ;再过点 作直线 的垂线交 轴于点 ,过点 作 轴的垂线交直线 于点 ;…;按此作法继续下去,则点 的坐标是.
20. 如图,已知直线 : ,过点 作直线 的垂线交 轴于点 ,过点 作 轴的垂线交直线 于点 ;再过点 作直线 的垂线交 轴于点 ,过点 作 轴的垂线交直线 于点 ;…;按此作法继续下去,则点 的坐标是.
三、解答题
-
21. 已知: , , 平分 .求: 的度数.22. 如图,AD⊥BC于D,BD=AC+DC,若∠BAC=110°,求∠C的度数.
 23. 在等腰三角形ABC中,三条边分别为a、b、c,已知a= 3,且b、c是关于x的方程x2+mx+2- =0的两个实数根、求△ABC的周长。
23. 在等腰三角形ABC中,三条边分别为a、b、c,已知a= 3,且b、c是关于x的方程x2+mx+2- =0的两个实数根、求△ABC的周长。四、作图题
-
24.
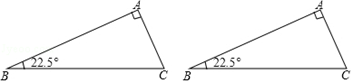 (1)、操作实践:△ABC中,∠A=90°,∠B=22.5°,请画出一条直线把△ABC分割成两个等腰三角形,并标出分割成两个等腰三角形底角的度数;(要求用两种不同的分割方法)(2)、分类探究:△ABC中,最小内角∠B=24°,若△ABC被一直线分割成两个等腰三角形,请画出相应示意图并写出△ABC最大内角的所有可能值;25.(1)、如图,AE是∠MAD的平分线,点C是AE上一点,点B是AM上一点,在AD上求作一点P,使得△ABC≌△APC,请保留清晰的作图痕迹.
(1)、操作实践:△ABC中,∠A=90°,∠B=22.5°,请画出一条直线把△ABC分割成两个等腰三角形,并标出分割成两个等腰三角形底角的度数;(要求用两种不同的分割方法)(2)、分类探究:△ABC中,最小内角∠B=24°,若△ABC被一直线分割成两个等腰三角形,请画出相应示意图并写出△ABC最大内角的所有可能值;25.(1)、如图,AE是∠MAD的平分线,点C是AE上一点,点B是AM上一点,在AD上求作一点P,使得△ABC≌△APC,请保留清晰的作图痕迹. (2)、如图a,在△ABC中, ∠ACB= 90°,∠A= 60°,BE、CF分别是∠ABC和∠ACB的角平分线,CF与BE相交于点O.请探究线段BC、BF、CE之间的关系,直接写出结论,不要求证明.
(2)、如图a,在△ABC中, ∠ACB= 90°,∠A= 60°,BE、CF分别是∠ABC和∠ACB的角平分线,CF与BE相交于点O.请探究线段BC、BF、CE之间的关系,直接写出结论,不要求证明.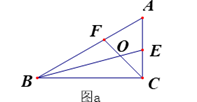 (3)、如图b,若(2)中∠ACB为任意角,其它条件不变,请探究BC、BF、CE之间又有怎样的关系,请证明你的结论.
(3)、如图b,若(2)中∠ACB为任意角,其它条件不变,请探究BC、BF、CE之间又有怎样的关系,请证明你的结论.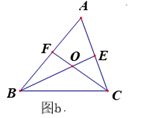
五、综合题
-
26. 有公共顶点A的△ABD,△ACE都是等边三角形.
 (1)、如图1,将△ACE绕顶点A旋转,当E,C,B共线时,求∠BCD的度数;(2)、如图2,将△ACE绕顶点A旋转,当∠ACD=90°时,延长EC角BD于F,
(1)、如图1,将△ACE绕顶点A旋转,当E,C,B共线时,求∠BCD的度数;(2)、如图2,将△ACE绕顶点A旋转,当∠ACD=90°时,延长EC角BD于F,①求证:∠DCF=∠BEF;
②写出线段BF与DF的数量关系,并说明理由.
27. 在直线上顺次取A,B,C三点,分别以AB,BC为边在直线的同侧作等边三角形,作得的两个等边三角形的另一顶点分别为D,E两点.连结DE.

 (1)、如图1所示,连结CD,AE,求证:CD = AE.(2)、如图2所示,若AB = 1,BC = 2,求证:∠BDE = 90°.(3)、如图3所示,将图2中的等边三角形BEC绕点B作适当的旋转,连结AE,若有DE 2 + BE 2 = AE 2 , 试求∠DEB的度数.28. 已知 中, ; 中, ; ,点A.D.E在同一直线上,AE与BC相交于点F,连接BE.
(1)、如图1所示,连结CD,AE,求证:CD = AE.(2)、如图2所示,若AB = 1,BC = 2,求证:∠BDE = 90°.(3)、如图3所示,将图2中的等边三角形BEC绕点B作适当的旋转,连结AE,若有DE 2 + BE 2 = AE 2 , 试求∠DEB的度数.28. 已知 中, ; 中, ; ,点A.D.E在同一直线上,AE与BC相交于点F,连接BE. (1)、如图1,当 时,
(1)、如图1,当 时,①请直接写出 和 的形状;
②求证: ;
③请求出 的度数.
(2)、如图2,当 时,请直接写出:① 的度数;
②若 , ,线段AF的长.
29. 如图 (1)、问题发现:如图1,如果 和 均为等边三角形 等边三角形的三条边都相等,三个角都是 ,点B、E、D三点在同一直线上,连接 则CD与BE的数量关系为; 的度数为度.(2)、探究:如图2,若 为三边互不相等的三角形,以它的边AB、AC为边分别向外作等边 与等边 ,连接BE和CD相交于点O , AB交CD于点F , AC交BE于G , 则CD与BE还相等吗?若相等,请证明,若不相等,说明理由:并请求出 的度数?
(1)、问题发现:如图1,如果 和 均为等边三角形 等边三角形的三条边都相等,三个角都是 ,点B、E、D三点在同一直线上,连接 则CD与BE的数量关系为; 的度数为度.(2)、探究:如图2,若 为三边互不相等的三角形,以它的边AB、AC为边分别向外作等边 与等边 ,连接BE和CD相交于点O , AB交CD于点F , AC交BE于G , 则CD与BE还相等吗?若相等,请证明,若不相等,说明理由:并请求出 的度数?