湘教版备考2021年中考数学二轮复习专题9分式

试卷更新日期：2021-04-26 类型：二轮复习

进入出卷网下载

一、单选题

1. 关于x ， y的方程xy﹣x+y＝﹣3的整数解（x ， y）的对数为（）

A、3 B、4 C、5 D、6

查看试题解析
2. 已知a＋ $\frac{1}{a}$ ＝ $\sqrt{10}$ ，则a－ $\frac{1}{a}$ 的值为（）

A、±2 $\sqrt{2}$ B、8 C、 $\sqrt{6}$ D、± $\sqrt{6}$

查看试题解析
3. 若 $x$ 是整数，则使分式 $\frac{8 x + 2}{2 x - 1}$ 的值为整数的 $x$ 值有（）个.

A、2 B、3 C、4 D、5

查看试题解析
4. 已知三个数 $a ， b ， c$ 满足 $\frac{a b}{a + b} = \frac{1}{5}$ ， $\frac{b c}{b + c} = \frac{1}{6}$ ， $\frac{c a}{c + a} = \frac{1}{7}$ ，则 $\frac{a b c}{a b + b c + c a}$ 的值是（）

A、 $\frac{1}{9}$ B、 $\frac{1}{6}$ C、 $\frac{2}{15}$ D、 $\frac{1}{20}$

查看试题解析
5. 若 $3^{x} + 3^{x} + 3^{x} + 3^{x} = \frac{4}{9}$ ，则 $x =$ （）

A、-2 B、-1 C、0 D、 $\frac{1}{4}$

查看试题解析
6. 已知公式 $\frac{1}{R} = \frac{1}{R_{1}} + \frac{1}{R_{2}}$ （ $R_{1} \neq R_{2}$ ），则表示 $R_{1}$ 的公式是（）

A、 $R_{1} = \frac{R_{2} - R}{R R_{2}}$ B、 $R_{1} = \frac{R R_{2}}{R - R_{2}}$ C、 $R_{1} = \frac{R (R_{1} + R_{2})}{R_{2}}$ D、 $R_{1} = \frac{R R_{2}}{R_{2} - R}$

查看试题解析
7. 关于 $x$ 的分式方程 $\frac{x + m}{x - 2} + \frac{2 m}{2 - x} = 3$ 的解为正实数，则实数 $m$ 的取值范围是 $($ $)$

A、 $m < - 6$ 且 $m \neq 2$ B、 $m > 6$ 且 $m \neq 2$ C、 $m < 6$ 且 $m \neq - 2$ D、 $m < 6$ 且 $m \neq 2$

查看试题解析
8. 若 $\frac{x + 2}{x^{2} - 2 x + 1}$ 的值为正数，则x的取值范围是（）

A、x＜－2 B、x＜1 C、x＞－2且x≠1 D、x＞1

查看试题解析
9. 将甲、乙、丙三个正分数化为最简分数后，其分子分别为6、15、10，其分母的最小公倍数为360．判断甲、乙、丙三数的大小关系为何？（）

A、乙＞甲＞丙 B、乙＞丙＞甲 C、甲＞乙＞丙 D、甲＞丙＞乙

查看试题解析
10. 张华在一次数学活动中，利用“在面积一定的矩形中，正方形的周长最短”的结论，推导出“式子x+ $\frac{1}{x}$ （x＞0）的最小值是2”．其推导方法如下：在面积是1的矩形中设矩形的一边长为x，则另一边长是 $\frac{1}{x}$ ，矩形的周长是2（x+ $\frac{1}{x}$ ）；当矩形成为正方形时，就有x= $\frac{1}{x}$ （0＞0），解得x=1，这时矩形的周长2（x+ $\frac{1}{x}$ ）=4最小，因此x+ $\frac{1}{x}$ （x＞0）的最小值是2．模仿张华的推导，你求得式子 $\frac{x^{2} + 9}{x}$ （x＞0）的最小值是（）

A、2 B、1 C、6 D、10

查看试题解析

二、填空题

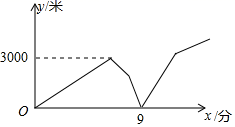
11. 某快递公司快递员甲匀速骑车去距公司6000米的某小区取物件，出发几分钟后，该公司快递员乙发现甲的手机落在公司，于是立马匀速骑车去追赶甲，乙出发几分钟后，甲也发现自己的手机落在了公司，立即调头以原速的2倍原路返回，1分钟后遇到了乙，乙把手机给甲后，乙以原速的一半原路返回公司，甲以返回时的速度继续去小区取物件，刚好在事先预计的时间到达该小区.甲、乙两人相距的路程y（米）与甲出发的时间x（分钟）之间的关系如图所示（给手机及中途其它耽误时间忽略不计），则甲到小区时，乙距公司的路程是米.

查看试题解析
12. 阅读材料：
分离整数法就是将分式拆分成一个整式与一个分式(分子为整数)的和的形式．如：

① $\frac{x + 1}{x - 1} = \frac{x - 1 + 2}{x - 1} = \frac{x - 1}{x - 1} + \frac{2}{x - 1} = 1 + \frac{2}{x - 1}$ ；

② $\frac{x^{2} + 1}{x - 3}$ = $\frac{x^{2} - 9 + 10}{x - 3}$ = $\frac{x^{2} - 9}{x - 3}$ + $\frac{10}{x - 3}$ =x+3+ $\frac{10}{x - 3}$ .

解答问题．已知x为整数，且分式 $\frac{3 x - 4}{x - 2}$ 为整数，则x的值为.

查看试题解析
13. 已知实数a，b，c满足 $\frac{a}{b + c} + \frac{b}{c + a} + \frac{c}{a + b} = 1$ ，则 $\frac{a^{2}}{b + c} + \frac{b^{2}}{c + a} + \frac{c^{2}}{a + b} =$ ．

查看试题解析
14. 请写出一个同时满足下列条件的分式：
（ 1 ）分式的值不可能为0；（2）分式有意义时，的取值范围是x≠±2；（3）当x=0时，分式的值为-1.你所写的分式为.

查看试题解析
15. 已知 $\frac{x}{x - 1} = \frac{y^{2} + 4 y - 2}{y^{2} + 4 y - 1}$ ，则的y²+4y+x值为．

查看试题解析
16. 一组按规律排列的式子： $- \frac{b^{2}}{a}$ ， $\frac{b^{5}}{a^{2}}$ ， $- \frac{b^{8}}{a^{3}}$ ， $\frac{b^{11}}{a^{4}}$ ，…（ab≠0），其中第7个式子是，第n个式子是（n为正整数）．

查看试题解析
17. 已知整数a，b满足（ $\frac{2}{9}$ ）^a•（ $\frac{3}{4}$ ）^b=8，则a﹣b= ．

查看试题解析
18. 若（2x﹣3）^x⁺⁵=1，则x的值为．

查看试题解析
19. 若关于x的方程 $\frac{x + 2}{x - 2} = \frac{m}{x - 2}$ 有增根，则m的值是．

查看试题解析
20. 如图，甲，乙两人分别从A、B两地同时出发去往C地，在距离C地2500米处甲追上乙；若乙提前10分钟出发，则在距离C地1000米处甲追上乙。已知，乙每分钟走60米，那么甲的速度是每分钟米。

查看试题解析

三、计算题

21. 已知 $a + b + c = 0$ ，且 $a b c \neq 0$ ，求： $a (\frac{1}{b} + \frac{1}{c}) + b (\frac{1}{a} + \frac{1}{c}) + c (\frac{1}{a} + \frac{1}{b})$ 的值.

查看试题解析
22. 设 $\frac{x}{x^{2} + x + 1}$ ＝a(a≠0)，求 $\frac{x^{2}}{x^{4} + x^{2} + 1}$ 的值．

查看试题解析

四、解答题

23. 扎西与卓玛共同清点一批图书，已知扎西清点完300本图书所用的时间与卓玛清点完200本所用的时间相同，扎西平均每分钟比卓玛多清点10本，求卓玛平均每分清点图书的数量?

查看试题解析
24. 列方程解应用题：
甲乙两站相距1200千米，货车与客车同时从甲站出发开往乙站，已知客车的速度是货车速度的2.5倍，结果客车比货车早6小时到达乙站，求客车与货车的速度分别是多少？

查看试题解析
25. 为配合“一带一路”国家倡议，某铁路货运集装箱物流园区正式启动了2期扩建工程．一项地基基础加固处理工程由A、B两个工程公司承担建设，已知A工程公司单独建设完成此项工程需要180天，A工程公司单独施工45天后，B工程公司参与合作，两工程公司又共同施工54天后完成了此项工程．

(1)、求B工程公司单独建设完成此项工程需要多少天？

(2)、由于受工程建设工期的限制，物流园区管委会决定将此项工程划包成两部分，要求两工程公司同时开工，A工程公司建设其中一部分用了m天完成，B工程公司建设另一部分用了n天完成，其中m，n均为正整数，且m＜46，n＜92，求A、B两个工程公司各施工建设了多少天？

查看试题解析

五、综合题

26. 小红到离家2100米的学校参加艺术节联欢会，到学校时发现演出道具忘在家中，此时距联欢会开始还有45分钟，于是她马上步行回家取道具，随后骑自行车返回学校.已知小红骑自行车到学校比她从学校步行到家用时少20分钟，且骑自行车的平均速度是步行平均速度的3倍.

(1)、小红步行的平均速度（单位：米/分）是多少？

(2)、小红能否在联欢会开始前赶到学校？（通过计算说明你的理由）

查看试题解析
27. 某经销商3月份用18000元购进一批T恤衫售完后，4月份用39000元购进单批相同的T恤衫，数量是3月份的2倍，但每件进价涨了10元.

(1)、4月份进了这批T恤衫多少件？

(2)、4月份，经销商将这批T恤衫平均分给甲、乙两家分店销售，每件标价180元.甲店按标价卖出a件以后，剩余的按标价八折全部售出；乙店同样按标价卖出a件，然后将b件按标价九折售出，再将剩余的按标价七折全部售出，结果利润与甲店相同.
①用含a的代数式表示b；

②已知乙店按标价售出的数量不超过九折售出的数量，请你求出乙店利润的最大值.

查看试题解析
28. 某商场购进甲、乙两种商品，甲种商品共用了 $2000$ 元，乙种商品共用了 $2400$ 元.已知乙种商品每件进价比甲种商品每件进价多 $10$ 元，且购进的甲、乙两种商品件数相同.

(1)、求甲、乙两种商品的每件进价；

(2)、该商场将购进的甲、乙两种商品进行销售，甲种商品的销售单价为 $60$ 元，乙种商品的销售单价为 $70$ 元，销售过程中发现甲种商品销量不好，商场决定：甲种商品销售一定数量后，将剩余的甲种商品按原销售单价的九折销售；乙种商品销售单价保持不变.要使两种商品全部售完后共获利不少于 $680$ 元，问甲种商品按原销售单价至少销售多少件？

查看试题解析
29. 某超市用5000元购进某种干果销售，由于销售状况良好，超市又调拨9000元资金购进该种干果，但这次每千克的进价比第一次的进价提高了5元，购进干果数量是第一次的1.5倍.

(1)、该种干果的第一次进价是每千克多少元？

(2)、如果超市按每千克40元的价格出售，当大部分干果售出后，余下的100千克按售价的6折售完，超市销售这种干果共盈利多少元？

(3)、如果这两批干果每千克售价相同，且全部售完后总利淘不低于25%，那么每千克干果的售价至少是多少元？

查看试题解析