浙江省绍兴市2021届高三下学期数学一模试卷
试卷更新日期:2021-04-26 类型:高考模拟
一、单选题
-
1. 已知集合 或 , ,则 ( )A、 B、 C、 D、2. 已知i是虚数单位,若 ,则 ( )A、 B、 C、 D、3. 若实数x,y满足约束条件 ,则 的最大值是( )A、 B、3 C、 D、44. 函数 的图象可能是( )A、
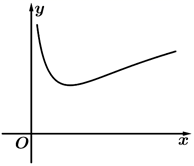 B、
B、 C、
C、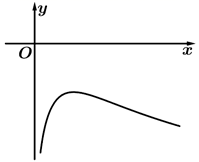 D、
D、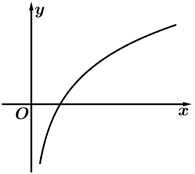 5. 某几何体由四棱锥和半个圆柱组合而成,其三视图如图所示,则该几何体的体积是( )
5. 某几何体由四棱锥和半个圆柱组合而成,其三视图如图所示,则该几何体的体积是( )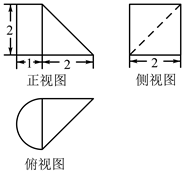 A、 B、 C、 D、6. 设 ,则“ ”是“直线 和圆 有公共点”的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件7. 已知无穷数列 是各项均为正数且公差不为零的等差数列,其前n项和为 ,则( )A、数列 不可能是等差数列 B、数列 不可能是等差数列 C、数列 不可能是等差数列 D、数列 不可能是等差数列8. 已知 ,则a+b的最小值是( )A、 B、3 C、 D、49. 已知椭圆 和点 ,若存在过点M的直线交C于P,Q两点,满足 ,则椭圆C的离心率取值范围是( )A、 B、 C、 D、10. 已知a,b , ,若关于x不等式 的解集为 ,则( )A、不存在有序数组 ,使得 B、存在唯一有序数组 ,使得 C、有且只有两组有序数组 ,使得 D、存在无穷多组有序数组 ,使得
A、 B、 C、 D、6. 设 ,则“ ”是“直线 和圆 有公共点”的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件7. 已知无穷数列 是各项均为正数且公差不为零的等差数列,其前n项和为 ,则( )A、数列 不可能是等差数列 B、数列 不可能是等差数列 C、数列 不可能是等差数列 D、数列 不可能是等差数列8. 已知 ,则a+b的最小值是( )A、 B、3 C、 D、49. 已知椭圆 和点 ,若存在过点M的直线交C于P,Q两点,满足 ,则椭圆C的离心率取值范围是( )A、 B、 C、 D、10. 已知a,b , ,若关于x不等式 的解集为 ,则( )A、不存在有序数组 ,使得 B、存在唯一有序数组 ,使得 C、有且只有两组有序数组 ,使得 D、存在无穷多组有序数组 ,使得二、填空题
-
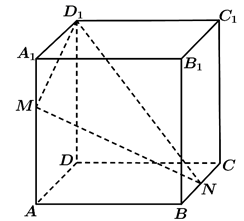
11. 《九章算术》中的“两鼠穿墙题”是我国数学的古典名题:“今有垣厚若干尺,两鼠对穿,大鼠日一尺,小鼠也日一尺,大鼠日自倍,小鼠日自半.问何日相逢,各穿几何?”题意是:有两只老鼠从墙的两边打洞穿墙,大老鼠第一天进一尺,以后每天加倍:小老鼠第一天也进一尺,以后每天减半.如果墙足够厚, 为前n天两只老鼠打洞长度之和,则 尺.12. 如图,在棱长为4的正方体 中,M是棱 上的动点,N是棱 的中点.当平面 与底面 所成的锐二面角最小时, .
 13. 已知平面向量 满足: ,则 的最大值是.14. 已知函数 ,则 ;关于x的不等式 的解集是.15. 已知二项展开式 ,则 ; .(用数字作答)16. 在锐角 中,内角A,B所对的边分别为a,b , 若 ,则 ;边长a的取值范围是.17. 袋中装有大小相同的1个白球和2个黑球,现分两步从中摸球:第一步从袋中随机摸取2个球后全部放回袋中(若摸得白球则涂成黑球,若摸得黑球则不变色);第二步再从袋中随机摸取2个球,记第二步所摸取的2个球中白球的个数为 ,则 ; .
13. 已知平面向量 满足: ,则 的最大值是.14. 已知函数 ,则 ;关于x的不等式 的解集是.15. 已知二项展开式 ,则 ; .(用数字作答)16. 在锐角 中,内角A,B所对的边分别为a,b , 若 ,则 ;边长a的取值范围是.17. 袋中装有大小相同的1个白球和2个黑球,现分两步从中摸球:第一步从袋中随机摸取2个球后全部放回袋中(若摸得白球则涂成黑球,若摸得黑球则不变色);第二步再从袋中随机摸取2个球,记第二步所摸取的2个球中白球的个数为 ,则 ; .三、解答题
-
18. 已领函数(1)、求 的值;(2)、求 在区间 上的最大值和最小值.19. 如图,在三棱柱 中, .
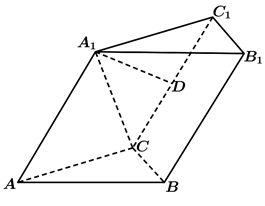 (1)、证明: 平面 ;(2)、设点D为 的中点,求直线 与平面 所成角的正弦值.20. 已知等差数列 的公差不为零, ,且 成等比数列,数列 的前n项和为 ,满足 .(1)、求数列 和 的通项公式;(2)、若数列 满足: ,求使得 成立的所有n值.
(1)、证明: 平面 ;(2)、设点D为 的中点,求直线 与平面 所成角的正弦值.20. 已知等差数列 的公差不为零, ,且 成等比数列,数列 的前n项和为 ,满足 .(1)、求数列 和 的通项公式;(2)、若数列 满足: ,求使得 成立的所有n值.