浙江省丽水市2020-2021学年七年级下学期数学期中考试试卷（一）

试卷更新日期：2021-04-25 类型：期中考试

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分）

1. 下列四个图形中，∠1和∠2是同位角的是（）

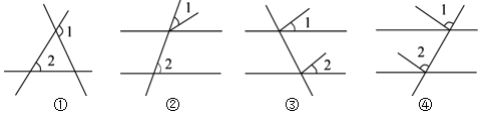A、②③ B、①②③ C、①②④ D、①④

查看试题解析
2. 下列结论错误的是（）

A、垂直于同一直线的两条直线互相平行 B、两直线平行，同旁内角互补 C、过直线外一点有且只有一条直线与这条直线平行 D、同一平面内，不相交的两条直线叫做平行线

查看试题解析
3. 若 $\frac{1}{2}$ a^3xb^y与﹣a^2yb^x⁺¹是同类项，则x ， y的值为（）

A、 ${\begin{matrix} x = - 2 \\ y = 3 \end{matrix}$ B、 ${\begin{matrix} x = 2 \\ y = - 3 \end{matrix}$ C、 ${\begin{matrix} x = - 2 \\ y = - 3 \end{matrix}$ D、 ${\begin{matrix} x = 2 \\ y = 3 \end{matrix}$

查看试题解析
4. 已知方程2x﹣3y＝7，用含x的代数式表示y为（）

A、y＝ $\frac{7 - 2 x}{3}$ B、y＝ $\frac{2 x - 7}{3}$ C、x＝ $\frac{7 + 3 y}{2}$ D、x＝ $\frac{7 - 3 y}{2}$

查看试题解析
5. 若 ${\begin{matrix} x = a \\ y = b \end{matrix}$ 是二元一次方程2x+y＝0的一个解（a≠0），则下列结论错误的是（）

A、a ， b异号 B、 $\frac{a}{b}$ ＝﹣2 C、2﹣6a﹣3b＝2 D、满足条件的数对（a ， b）有无数对

查看试题解析
6. 在育才社团活动中，为培养学生动手操作能力，发展学生思维能力，王老师让学生把5m长的彩绳截成2m或1m的彩绳，用来做手工编织，在不造成浪费的前提下，不同的截法有（）

A、1 种 B、2 种 C、3 种 D、4 种

查看试题解析
7. 如图，AB∥EF∥CD ， AD∥BC ， BD平分∠ABC ，则图中与∠EOD相等的角有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
8. 如图，AB∥ED ， α＝∠A+∠E ， β＝∠B+∠C+∠D ，则β与α的数量关系是（）

A、2β＝3α B、β＝2α C、2β＝5α D、β＝3α

查看试题解析
9. 若 ${\begin{matrix} 2 x - y = a \\ 3 x + 2 y = 5 a \end{matrix}$ ，且a≠0，则 $\frac{x}{y}$ 的值为（）

A、1 B、﹣1 C、 $\frac{1}{2}$ D、﹣ $\frac{1}{2}$

查看试题解析
10. 已知关于x ， y的方程组 ${\begin{matrix} x + 3 y = 4 - a \\ x - y = 3 a \end{matrix}$ ，给出下列结论：①不论a取何值，方程组总有一组解；②当a＝﹣2时，x ， y的值互为相反数；③x+2y＝3；④当3^x^+y＝81时，a＝2．其中正确的是（）

A、①②③④ B、①②③ C、②③ D、①③④

查看试题解析

二、填空题（本题有6小题，每小题4分，共24分）

11. 若（m﹣2）x﹣2y^|m^﹣^1|＝3是关于x ， y的二元一次方程，则m＝．

查看试题解析
12. 已知直线l₁∥l₂ ，一块含45°角的直角三角板按如图方式放置，∠1＝55°，则∠2＝．

查看试题解析
13. 如图，把一张长方形纸条ABCD沿AF折叠，点B的对应点为点E ．已知∠ADB＝25°，AE∥BD ，则∠BAF＝．

查看试题解析
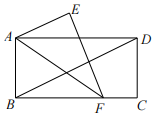14. 声音在空气中的传播速度v（m/s）随温度t（℃）的变化而变化，且v＝at+b（a ， b是常数）．若当t＝10时，v＝336；当t＝20时，v＝342．则当v＝324时，t＝．

查看试题解析
15. 如图是一块长方形场地ABCD ，长AB＝am ，宽AD＝bm ，从A ， B两处入口的小路宽都为1m ，两小路汇合处路宽为2m ，其余部分种植草坪，则草坪的面积为m² ．（用含a ， b的代数式表示）

查看试题解析
16. 若关于x ， y的 ${\begin{matrix} a_{1} x + b_{1} y = c_{1} \\ a_{2} x + b_{2} y = c_{2} \end{matrix}$ 的解是 ${\begin{matrix} x = 2 \\ y = - 3 \end{matrix}$ ，则关于m ， n的方程组 ${\begin{matrix} 2 a_{1} (m - n) - 3 b_{1} (m + n) = 5 c_{1} \\ 2 a_{2} (m - n) - 3 b_{2} (m + n) = 5 c_{2} \end{matrix}$ 的解是．

查看试题解析

三、解答题（本题有7小题，共66分。）

17. 解下列方程组：

(1)、 ${\begin{matrix} 3 x + 2 y = 5 \\ 2 x - y = 1 \end{matrix}$ ；

(2)、 ${\begin{matrix} 3 (x + y) - 4 (x - y) = 4 \\ \frac{x + y}{2} + \frac{x - y}{6} = 1 \end{matrix}$ ．

查看试题解析
18. 如图，CD是∠ACB的平分线，∠ACB＝82°，∠B＝48°，DE∥BC ．求∠EDC和∠BDC的度数．

查看试题解析
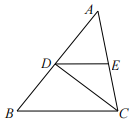19. 已知关于x ， y的方程组 ${\begin{matrix} a x + 5 y = 15 ① \\ 4 x - b y = - 2 ② \end{matrix}$ ，由于甲看错了方程①中的a ，得到方程组的解为 ${\begin{matrix} x = - 3 \\ y = - 1 \end{matrix}$ ，乙看错了方程②中的b ，得到方程组的解为 ${\begin{matrix} x = 5 \\ y = 2 \end{matrix}$ ，求原方程组的正确解．

查看试题解析
20. 如图，在三角形ABC中，AD⊥BC于点D ， EF⊥BC于点F ， ∠B＝∠GDC ．请说明∠1＝∠2的理由．

查看试题解析
21. 如图，已知方格纸的每一横行中从第二（从左往右）个数起的数都比它左边相邻的数大m ，各竖列中从第二（从上往下）个数起的数都比它上边相邻的数大n ．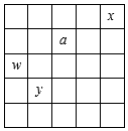

(1)、若a＝8，x＝12，y＝9，求m ， n的值；

(2)、若w＝0，求x与a的数量关系．

查看试题解析
22. 我市某包装生产企业承接了一批礼品盒制作业务，为了确保质量，该企业进行试生产．他们购得规格是170cm×40cm的标准板材作为原材料，每张标准板材再按照裁法一或裁法二裁下A型与B型两种板材（不计损耗），如图甲．（单位：cm）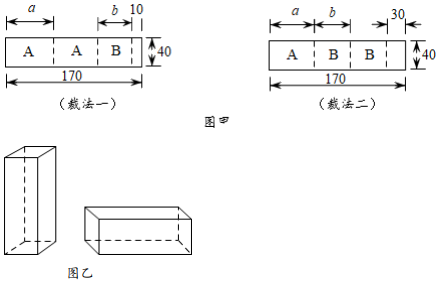

(1)、列出方程（组），求出图甲中a与b的值；

(2)、在试生产阶段，若将30张标准板材用裁法一裁剪，4张标准板材用裁法二裁剪，再将得到的A型与B型板材做侧面和底面，做成图乙的竖式（高大于长）与横式（长大于高）两种无盖礼品盒．
①两种裁法共生产A型板材张，B型板材张；

②能否在做成若干个上述的两种无盖礼品盒后，恰好把①中的A型板材和B型板材用完？若能，则竖式无盖礼品盒与横式无盖礼品盒分别做了几个？若不能，则最多能做成竖式和横式两种无盖礼品盒共多少个？并直接写出此时做成的横式无盖礼品盒的个数．

查看试题解析
23. 如图，已知直线BC∥OA ， ∠C＝∠OAB＝108°，E ， F在线段BC上（不与点B ， C重合），且满足∠FOB＝∠AOB ， OE平分∠COF ．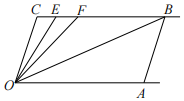

(1)、问：OC与AB是否平行？并说明理由；

(2)、求∠EOB的度数；

(3)、若左右平移线段AB ，是否存在∠OEC＝2∠OBA？若存在，求出此时∠OEC的度数；若不存在，请说明理由．

查看试题解析