浙江省丽水市2020-2021学年八年级下学期数学期中考试试卷(一)
试卷更新日期:2021-04-25 类型:期中考试
一、选择题(本题有10小题,每小题3分,共30分)
-
1. 下列方程是一元二次方程的是( )A、y+1=2 B、3x+2y=1 C、x2=5x D、xy=52. 下列根式是最简二次根式的是( )A、 B、 C、 D、3. 将一元二次方程3x2﹣2x=6化为一般形式,若二次项系数为3,则一次项系数和常数项分别为( )A、﹣2,6 B、﹣2,﹣6 C、2,6 D、2,﹣64. 下列计算正确的是( )A、 =±5 B、3 ﹣ =2 C、(﹣ )2=﹣5 D、 ÷ =45. 当用配方法解方程x2+2x﹣1=0时,配方结果正确的是( )A、(x+2)2=2 B、(x+1)2=2 C、(x+2)2=3 D、(x+1)2=36. 某基金2019年总投入10.8万元,到2021年总额预计达到14万元,设该基金的年平均涨幅为x , 则可列方程为( )A、10.8(1+x)=14 B、10.8(1+2x)=14 C、10.8(1+x)2=14 D、10.8(1+x+x2 )=147. 若x , y为实数,且y=2+ + ,则|x+y|的值是( )A、5 B、3 C、2 D、18. 若关于x的一元二次方程mx2+4x+1=0无实数根,则一次函数y=(4﹣m)x﹣m不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 如图,小梦要测量学校旗杆的高度BD , 在点A处测得∠BAD=45°,在点C处测得∠BCD=60°.已知AC=8米,点 A、C、D在同一直线上,则旗杆的高度BD为( )
 A、(4 +4)米 B、(7 +7)米 C、(14 +14)米 D、(4 +12)米10. 《周髀算经》中有一种几何方法可以用来解形如x(x+5)=24的方程的正数解,方法为:如图,将四个长为x+5,宽为x的长方形纸片(面积均为24)拼成一个大正方形,于是大正方形的面积为24×4+25=121,边长为11,故得x(x+5)=24的正数解为x= =3.小明按此方法解关于x的方程x2+mx﹣n=0时,构造出图形.已知大正方形的面积为10,小正方形的面积为4,则( )
A、(4 +4)米 B、(7 +7)米 C、(14 +14)米 D、(4 +12)米10. 《周髀算经》中有一种几何方法可以用来解形如x(x+5)=24的方程的正数解,方法为:如图,将四个长为x+5,宽为x的长方形纸片(面积均为24)拼成一个大正方形,于是大正方形的面积为24×4+25=121,边长为11,故得x(x+5)=24的正数解为x= =3.小明按此方法解关于x的方程x2+mx﹣n=0时,构造出图形.已知大正方形的面积为10,小正方形的面积为4,则( )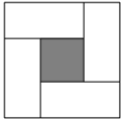 A、m=2,n= B、m= ,n=2 C、m= ,n=2 D、m=7,n=
A、m=2,n= B、m= ,n=2 C、m= ,n=2 D、m=7,n=二、填空题(本题有6小题,每小题4分,共24分)
-
11. 若式子 有意义,则x的取值范围是.12. 比较大小:﹣ ﹣2 .(填“>”或“<”)13. 已知实数a在数轴上的位置如图所示,化简|a+1|+ 的结果是 .
 14. 已知一元二次方程2x2+bx+c=0的两个根为x1=1和x2=2,则b= , c= .15. 已知关于x的一元二次方程(m﹣1)2x2+3mx+3=0有一个实数根为﹣1,则该方程的另一个实数根为 .16. 对于实数m , n , 我们定义一种运算为:m※n=mn+m﹣n , 则(a+b)※(a﹣b)= , 则方程x※(2※x)=﹣3的解是 .
14. 已知一元二次方程2x2+bx+c=0的两个根为x1=1和x2=2,则b= , c= .15. 已知关于x的一元二次方程(m﹣1)2x2+3mx+3=0有一个实数根为﹣1,则该方程的另一个实数根为 .16. 对于实数m , n , 我们定义一种运算为:m※n=mn+m﹣n , 则(a+b)※(a﹣b)= , 则方程x※(2※x)=﹣3的解是 .三、解答题(本题有8小题,共66分。)
-
17. 计算:(1)、 × ﹣ .(2)、( +1)( ﹣1)﹣( ﹣ )2 .18. 解方程:(1)、x2+2x﹣3=0;
(2)、(2x﹣1)2=2(2x﹣1).
19. 在如图所示的方格图中,每个小方格的边长均为1,则△ABC的周长为多少? 20. 已知x= +1,y= ﹣1,求x2+2xy+y2的值.21. 已知关于x的方程x(kx﹣4)﹣x2+4=0.(1)、若此方程有两个不相等的实数根,求k的取值范围;(2)、当k取何值时,此方程有两个相等的实数根,并求出这两个根.22. 如图,某水库大坝的横截面是梯形,其迎水坡AD的坡比为4:3,背水坡BC的坡比为1:2,大坝的高为20m , 坝顶CD的宽为10m . 求大坝横截面的周长.
20. 已知x= +1,y= ﹣1,求x2+2xy+y2的值.21. 已知关于x的方程x(kx﹣4)﹣x2+4=0.(1)、若此方程有两个不相等的实数根,求k的取值范围;(2)、当k取何值时,此方程有两个相等的实数根,并求出这两个根.22. 如图,某水库大坝的横截面是梯形,其迎水坡AD的坡比为4:3,背水坡BC的坡比为1:2,大坝的高为20m , 坝顶CD的宽为10m . 求大坝横截面的周长.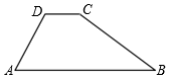 23. 某水果店销售一批草莓,草莓的进价为10元/千克,市场调研发现:当草莓的售价为15元/千克时,平均每天能售出8千克,而当草莓的售价每降0.5元/千克时,平均每天能多售出4千克.(1)、当草莓的售价定为12元/千克时,求该水果店每天草莓的销售量和销售利润.(2)、该水果店想在每天成本不超过200元的情况下,使得每天草莓的销售利润达到64元,售价应定为多少?24. 如图,在△ABC中,∠B=90°,cm , AB=6 cm , BC=6cm,点P从点A出发,以每秒 cm的速度沿AB匀速运动,同时点Q从点B出发以每秒3cm的速度沿B→C→A匀速运动,当有一点停止运动时,另一点也停止运动,设运动时间为t秒.
23. 某水果店销售一批草莓,草莓的进价为10元/千克,市场调研发现:当草莓的售价为15元/千克时,平均每天能售出8千克,而当草莓的售价每降0.5元/千克时,平均每天能多售出4千克.(1)、当草莓的售价定为12元/千克时,求该水果店每天草莓的销售量和销售利润.(2)、该水果店想在每天成本不超过200元的情况下,使得每天草莓的销售利润达到64元,售价应定为多少?24. 如图,在△ABC中,∠B=90°,cm , AB=6 cm , BC=6cm,点P从点A出发,以每秒 cm的速度沿AB匀速运动,同时点Q从点B出发以每秒3cm的速度沿B→C→A匀速运动,当有一点停止运动时,另一点也停止运动,设运动时间为t秒. (1)、当t=1时,直接写出P , Q两点间的距离.(2)、是否存在t , 使得△BPQ的面积是△ABC面积的 ?若存在,请求出t的值;若不存在,请说明理由.(3)、当△BPQ为直角三角形时,求t的取值范围.
(1)、当t=1时,直接写出P , Q两点间的距离.(2)、是否存在t , 使得△BPQ的面积是△ABC面积的 ?若存在,请求出t的值;若不存在,请说明理由.(3)、当△BPQ为直角三角形时,求t的取值范围.