四川省宜宾市叙州区2021届九年级下学期数学期中考试试卷
试卷更新日期:2021-04-25 类型:期中考试
一、选择题:本大题共12个小题,每小题4分,共48分.
-
1. 6的相反数是( )A、6 B、﹣6 C、 D、﹣2. 我国自主研发的北斗系统技术世界领先,2020年6月23日在西昌卫星发射中心成功发射最后一颗北斗三号组网卫星,该卫星发射升空的速度约为7100米/秒.将7100用科学记数法表示为( )A、7100 B、0.71×104 C、71×102 D、7.1×1033. 一个立体图形的三视图如图所示,则该立体图形是( )
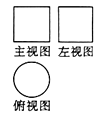 A、圆柱 B、圆锥 C、长方体 D、球4. 一元二次方程x2﹣2x=0的两根分别为x1和x2 , 则x1x2为( )A、﹣2 B、1 C、2 D、05. 不等式组 的解集在数轴上表示正确的是( )A、
A、圆柱 B、圆锥 C、长方体 D、球4. 一元二次方程x2﹣2x=0的两根分别为x1和x2 , 则x1x2为( )A、﹣2 B、1 C、2 D、05. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、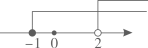 D、
D、 6. 在▱ABCD中,若∠BAD与∠CDA的角平分线交于点E,则△AED的形状是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定7. 7名学生的鞋号(单位:厘米)由小到大是:20,21,22,22,22,23,23,则这组数据的众数和中位数分别是( )A、20,21 B、21,22 C、22,22 D、22,238. 如图,M、N分别是△ABC的边AB、AC的中点,若∠A=65°,∠ANM=45°,则∠B=( )
6. 在▱ABCD中,若∠BAD与∠CDA的角平分线交于点E,则△AED的形状是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定7. 7名学生的鞋号(单位:厘米)由小到大是:20,21,22,22,22,23,23,则这组数据的众数和中位数分别是( )A、20,21 B、21,22 C、22,22 D、22,238. 如图,M、N分别是△ABC的边AB、AC的中点,若∠A=65°,∠ANM=45°,则∠B=( ) A、20° B、45° C、65° D、70°9. 学校为了丰富学生知识,需要购买一批图书,其中科普类图书平均每本的价格比文学类图书平均每本的价格多8元,已知学校用15000元购买科普类图书的本数与用12000元购买文学类图书的本数相等.设文学类图书平均每本x元,则列方程正确的是( )A、 = B、 = C、 = D、 = +810. 如图,在矩形ABCD中BC=8,CD=6,将△ABE沿BE折叠,使点A恰好落在对角线BD上F处,则DE的长是( )
A、20° B、45° C、65° D、70°9. 学校为了丰富学生知识,需要购买一批图书,其中科普类图书平均每本的价格比文学类图书平均每本的价格多8元,已知学校用15000元购买科普类图书的本数与用12000元购买文学类图书的本数相等.设文学类图书平均每本x元,则列方程正确的是( )A、 = B、 = C、 = D、 = +810. 如图,在矩形ABCD中BC=8,CD=6,将△ABE沿BE折叠,使点A恰好落在对角线BD上F处,则DE的长是( )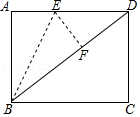 A、3 B、 C、5 D、11. 如图,△ABC和△ECD都是等边三角形,且点B,C,D在一条直线上,连结BE、AD,点M、N分别是线段BE、AD上的两点,且BM= BE,AN= AD,则△CMN的形状是( )
A、3 B、 C、5 D、11. 如图,△ABC和△ECD都是等边三角形,且点B,C,D在一条直线上,连结BE、AD,点M、N分别是线段BE、AD上的两点,且BM= BE,AN= AD,则△CMN的形状是( )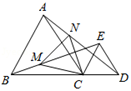 A、等腰三角形 B、直角三角形 C、等边三角形 D、不等边三角形12. 函数y=ax2+bx+c(a≠0)的图象与x轴交于点(2,0),顶点坐标为(﹣1,n),其中n>0.以下结论正确的是( )
A、等腰三角形 B、直角三角形 C、等边三角形 D、不等边三角形12. 函数y=ax2+bx+c(a≠0)的图象与x轴交于点(2,0),顶点坐标为(﹣1,n),其中n>0.以下结论正确的是( )①abc>0;②函数y=ax2+bx+c(a≠0)在x=1和x=﹣2处的函数值相等;③函数y=kx+1的图象与y=ax2+bx+c(a≠0)的函数图象总有两个不同交点;④函数y=ax2+bx+c(a≠0)在﹣3≤x≤3内既有最大值又有最小值.
A、①③ B、①②③ C、①④ D、②③④二、填空题:本大题共6个小题,每小题4分,共24分.
-
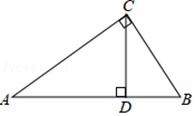
13. 分解因式:2a3b﹣4a2b2+2ab3= .14. 不等式组1< x﹣2≤2的所有整数解的和为.15. 将抛物线 的图象,向左平移1个单位,再向下平移2个单位,所得图象的解析式为 .16. 如图,已知直角△ABC中,CD是斜边AB上的高,AC=4,BC=3,则AD= .
 17. 如图,AB是半圆的直径,AC是一条弦,D是 的中点,DE⊥AB于点E且DE交AC于点F , DB交AC于点G , 若 = ,则 = .
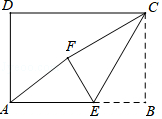
17. 如图,AB是半圆的直径,AC是一条弦,D是 的中点,DE⊥AB于点E且DE交AC于点F , DB交AC于点G , 若 = ,则 = .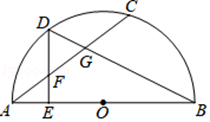 18. 如图,在矩形ABCD中,AB=3,CB=2,点E为线段AB上的动点,将△CBE沿CE折叠,使点B落在矩形内点F处,下列结论正确的是(写出所有正确结论的序号)
18. 如图,在矩形ABCD中,AB=3,CB=2,点E为线段AB上的动点,将△CBE沿CE折叠,使点B落在矩形内点F处,下列结论正确的是(写出所有正确结论的序号)①当E为线段AB中点时,AF∥CE;
②当E为线段AB中点时,AF= ;
③当A、F、C三点共线时,AE= ;
④当A、F、C三点共线时,△CEF≌△AEF .
三、解答题:本大题共7个小题,共78分.
-
19.(1)、计算: ;(2)、化简: ÷(1﹣ ).20. 如图,AB=AD , AC=AE , ∠BAE=∠DAC . 求证:∠C=∠E .
 21. 某校在七、八、九三个年级中进行“一带一路”知识竞赛,分别设有一等奖、二等奖、三等奖、优秀奖、纪念奖.现对三个年级同学的获奖情况进行了统计,其中获得纪念奖有17人,获得三等奖有10人,并制作了如图不完整的统计图.
21. 某校在七、八、九三个年级中进行“一带一路”知识竞赛,分别设有一等奖、二等奖、三等奖、优秀奖、纪念奖.现对三个年级同学的获奖情况进行了统计,其中获得纪念奖有17人,获得三等奖有10人,并制作了如图不完整的统计图. (1)、求三个年级获奖总人数;(2)、请补全扇形统计图的数据;(3)、在获一等奖的同学中,七年级和八年级的人数各占 ,其余为九年级的同学,现从获一等奖的同学中选2名参加市级比赛,通过列表或者树状图的方法,求所选出的2人中既有七年级又有九年级同学的概率.22. 如图,AB和CD两幢楼地面距离BC为30 米,楼AB高30米,从楼AB的顶部点A测得楼CD的顶部点D的仰角为45°.
(1)、求三个年级获奖总人数;(2)、请补全扇形统计图的数据;(3)、在获一等奖的同学中,七年级和八年级的人数各占 ,其余为九年级的同学,现从获一等奖的同学中选2名参加市级比赛,通过列表或者树状图的方法,求所选出的2人中既有七年级又有九年级同学的概率.22. 如图,AB和CD两幢楼地面距离BC为30 米,楼AB高30米,从楼AB的顶部点A测得楼CD的顶部点D的仰角为45°.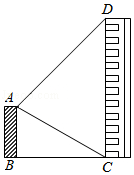 (1)、求∠CAD的大小;(2)、求楼CD的高度(结果保留根号).23. 如图,已知反比例函数y= (k>0)的图象和一次函数y=﹣x+b的图象都过点P(1,m),过点P作y轴的垂线,垂足为A , O为坐标原点,△OAP的面积为1.
(1)、求∠CAD的大小;(2)、求楼CD的高度(结果保留根号).23. 如图,已知反比例函数y= (k>0)的图象和一次函数y=﹣x+b的图象都过点P(1,m),过点P作y轴的垂线,垂足为A , O为坐标原点,△OAP的面积为1.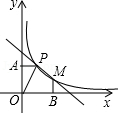 (1)、求反比例函数和一次函数的解析式;(2)、设反比例函数图象与一次函数图象的另一交点为M , 过M作x轴的垂线,垂足为B , 求五边形OAPMB的面积.24. 如图,线段AB经过⊙O的圆心O , 交⊙O于A、C两点,BC=1,AD为⊙O的弦,连结BD , ∠BAD=∠ABD=30°,连结DO并延长交⊙O于点E , 连结BE交⊙O于点M .
(1)、求反比例函数和一次函数的解析式;(2)、设反比例函数图象与一次函数图象的另一交点为M , 过M作x轴的垂线,垂足为B , 求五边形OAPMB的面积.24. 如图,线段AB经过⊙O的圆心O , 交⊙O于A、C两点,BC=1,AD为⊙O的弦,连结BD , ∠BAD=∠ABD=30°,连结DO并延长交⊙O于点E , 连结BE交⊙O于点M .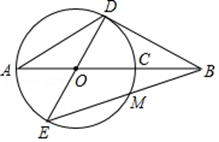 (1)、求证:直线BD是⊙O的切线;(2)、求⊙O的半径OD的长;(3)、求线段BM的长.25. 在平面直角坐标系xOy中,已知抛物线的顶点坐标为(2,0),且经过点(4,1),如图,直线y= x与抛物线交于A、B两点,直线l为y=﹣1.
(1)、求证:直线BD是⊙O的切线;(2)、求⊙O的半径OD的长;(3)、求线段BM的长.25. 在平面直角坐标系xOy中,已知抛物线的顶点坐标为(2,0),且经过点(4,1),如图,直线y= x与抛物线交于A、B两点,直线l为y=﹣1. (1)、求抛物线的解析式;(2)、在l上是否存在一点P , 使PA+PB取得最小值?若存在,求出点P的坐标;若不存在,请说明理由.(3)、知F(x0 , y0)为平面内一定点,M(m , n)为抛物线上一动点,且点M到直线l的距离与点M到点F的距离总是相等,求定点F的坐标.
(1)、求抛物线的解析式;(2)、在l上是否存在一点P , 使PA+PB取得最小值?若存在,求出点P的坐标;若不存在,请说明理由.(3)、知F(x0 , y0)为平面内一定点,M(m , n)为抛物线上一动点,且点M到直线l的距离与点M到点F的距离总是相等,求定点F的坐标.