宁夏银川市贺兰县2020-2021学年七年级下学期数学期中考试试卷
试卷更新日期:2021-04-25 类型:期中考试
一、选择题(共8小题,每小题3分,共24分)
-
1. 下列计算结果正确的是( )A、3a﹣(﹣a)=2a B、a3×(﹣a)2=a5 C、a5÷a=a5 D、(﹣a2)3=a62. 如果(ambn)3=a9b12 , 那么m , n的值分别为( )A、9,4 B、3,4 C、4,3 D、9,63. 如图,过点A的一次函数的图象与正比例函数y=2x的图象相交于点B , 则这个一次函数的解析式是( )
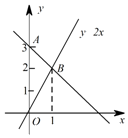 A、y=2x+3 B、y=x﹣3 C、y=2x﹣3 D、y=﹣x+34. 下列运算正确的是( )A、a2⋅a3=a6 B、a8÷a4=a2 C、a3+a3=2a6 D、(a2)3=a65. 如图所示,下列结论中不正确的是
A、y=2x+3 B、y=x﹣3 C、y=2x﹣3 D、y=﹣x+34. 下列运算正确的是( )A、a2⋅a3=a6 B、a8÷a4=a2 C、a3+a3=2a6 D、(a2)3=a65. 如图所示,下列结论中不正确的是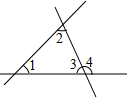 A、 和 是同位角 B、 和 是同旁内角 C、 和 是同位角 D、 和 是内错角6. 如图,直角边长为1的等腰直角三角形与边长为2的正方形在同一水平线上,三角形沿水平线从左向右匀速穿过正方形.设穿过时间为t , 正方形与三角形不重合部分的面积为S(阴影部分),则S与t的大致图象为( )
A、 和 是同位角 B、 和 是同旁内角 C、 和 是同位角 D、 和 是内错角6. 如图,直角边长为1的等腰直角三角形与边长为2的正方形在同一水平线上,三角形沿水平线从左向右匀速穿过正方形.设穿过时间为t , 正方形与三角形不重合部分的面积为S(阴影部分),则S与t的大致图象为( ) A、
A、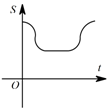 B、
B、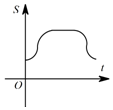 C、
C、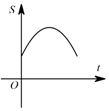 D、
D、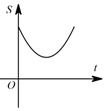 7. 如图,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=35°,则∠2的度数为( )
7. 如图,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=35°,则∠2的度数为( )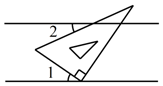 A、10° B、20° C、25° D、30°8. 电子文件的大小常用 等作为单位,其中 ,某视频文件的大小约为 等于( )A、 B、 C、 D、
A、10° B、20° C、25° D、30°8. 电子文件的大小常用 等作为单位,其中 ,某视频文件的大小约为 等于( )A、 B、 C、 D、二、填空题(共8小题,每小题3分,共24分)
-
9. 当x时,(x﹣4)0等于1.10. 将x2+6x+3配方成(x+m)2+n的形式,则m= .
11. 若an﹣3⋅a2n+1=a10 , 则n= .12. 已知y是关于x的函数,函数图象如图所示,则当y>0时,自变量x的取值范围是 .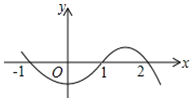 13. 若平面上4条直线两两相交,且无三条共线,则一共有对同旁内角.14. 如果x+y=1,x2+y2=3,那么x3+y3= .15. 82014×(﹣0.125)2015= .16. 已知正整数a , b , c(其中a≠1)满足abc=ab+50,则a+b+c的最小值是 , 最大值是 .
13. 若平面上4条直线两两相交,且无三条共线,则一共有对同旁内角.14. 如果x+y=1,x2+y2=3,那么x3+y3= .15. 82014×(﹣0.125)2015= .16. 已知正整数a , b , c(其中a≠1)满足abc=ab+50,则a+b+c的最小值是 , 最大值是 .三、解答题(共10小题;共72分)
-
17. 写出下列各问题所列的关系式中的常量与变量:(1)、时针旋转一周内,旋转的角度n(度)与旋转所需要的时间t(分)之间的关系式n=6t;
(2)、一辆汽车以40千米/时的速度向前匀速直线行驶时,汽车行驶的路程s(千米)与行驶时间t(时)之间的关系式s=40t .
18. 如图,点A表示小明家,点B表示小明外婆家,若小明先去外婆家拿渔具,然后再去河边钓鱼,怎样走路程最短,请画出行走路径,并说明理由. 19. 若xn=3,yn=4,求(2xn)2⋅2yn的值.20.
19. 若xn=3,yn=4,求(2xn)2⋅2yn的值.20.请用学过的方法研究一类新函数y= (k为常数,k≠0)的图象和性质.
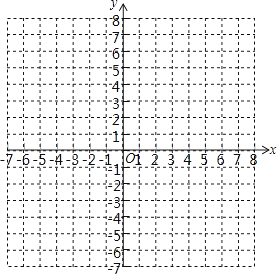 (1)、在给出的平面直角坐标系中画出函数y= 的图象;(2)、对于函数y= ,当自变量x的值增大时,函数值y怎样变化?21. 如果 ,求m , a , b的值.22. 阅读:已知a+b=﹣4,ab=3,求a2+b2的值.
(1)、在给出的平面直角坐标系中画出函数y= 的图象;(2)、对于函数y= ,当自变量x的值增大时,函数值y怎样变化?21. 如果 ,求m , a , b的值.22. 阅读:已知a+b=﹣4,ab=3,求a2+b2的值.解:∵a+b=﹣4,ab=3,
∴a2+b2=(a+b)2﹣2ab=(﹣4)2﹣2×3=10.
已知a+b=6,ab=2,请你根据上述解题思路求下列各式的值.
(1)、a2+b2;(2)、(a﹣b)2;
(3)、a2﹣ab+b2 .
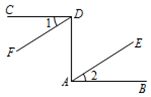
23. 如图,AB⊥AD , CD⊥AD , ∠1=∠2,求证:DF∥EA .
 24. 如图,已知正方形ABCD和ECGF的边长分别为a , b , a+b=17,ab=60,求阴影部分的面积.
24. 如图,已知正方形ABCD和ECGF的边长分别为a , b , a+b=17,ab=60,求阴影部分的面积.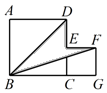 25. 如图,指出图中直线AC , BC被直线AB所截的同位角、内错角、同旁内角.
25. 如图,指出图中直线AC , BC被直线AB所截的同位角、内错角、同旁内角.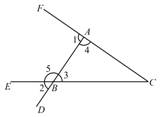 26. 在前面的学习中,我们通过对同一面积的不同表达和比较,利用图1和图2发现并验证了平方差公式和完全平方公式,不仅更清晰地“看到“公式的结构,同时感受到这样的抽象代数运算也有直观的背景.这种利用面积关系解决问题的方法,使抽象的数量关系因几何直观而形象化.请你利用上述方法解决下列问题:
26. 在前面的学习中,我们通过对同一面积的不同表达和比较,利用图1和图2发现并验证了平方差公式和完全平方公式,不仅更清晰地“看到“公式的结构,同时感受到这样的抽象代数运算也有直观的背景.这种利用面积关系解决问题的方法,使抽象的数量关系因几何直观而形象化.请你利用上述方法解决下列问题: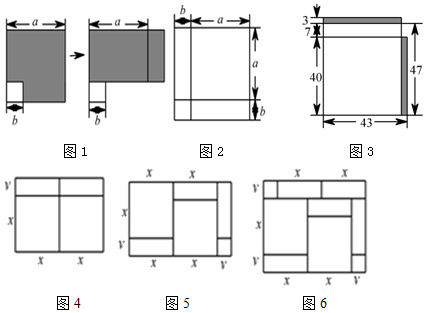 (1)、请写出图4、图5、图6所表示的代数恒等式.
(1)、请写出图4、图5、图6所表示的代数恒等式.
(2)、试画出一个几何图形,使它的面积能表示(x+y)(x+3y)=x2+4xy+3y2 .(3)、【拓展应用】提出问题:47×43,56×54,79×71,⋯⋯是一些十位数字相同,且个位数字之和是10的两个两位数相乘的算式,是否可以找到一种速算方法?几何建模:用矩形的面积表示两个正数的乘积,以47×43为例:
画长为47,宽为43的矩形,如图3,将这个47×43的矩形从右边切下长40,宽3的一条,拼接到原矩形的上面.
分析:几何建模步骤原矩形面积可以有两种不同的表达方式,47×43的矩形面积或(40+7+3)×40的矩形与右上角3×7的矩形面积之和,即47×43=(40+10)×40+3×7=5×4×100+3×7=2021,用文字表述47×43的速算方法是:十位数字4加1的和与4相乘,再乘以100,加上个位数字3与7的积,构成运算结果.请你参照上述几何建模步骤,计算57×53.要求画出示意图,写出几何建模步骤(标注有关线段).归纳提炼:两个十位数字相同,并且个位数字之和是10的两位数相乘的速算方法是 (用文字表述):证明上述速算方法的正确性.