宁夏银川市贺兰县2020-2021学年八年级下学期数学期中考试试卷

试卷更新日期：2021-04-25 类型：期中考试

进入出卷网下载

一、选择题（共8小题，每小题3分，共24分）

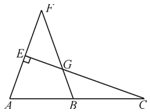
1. 已知a＞b，若c是任意实数，则下列不等式中总是成立的是（　　）

A、a+c＜b+c B、a﹣c＞b﹣c C、ac＜bc D、ac＞bc

查看试题解析
2. 下列x的值不是不等式﹣2x+4＜0的解的是（）

A、﹣2 B、3 C、3.5 D、10

查看试题解析
3. 如图，在△ABC中，∠B＝70°，∠C＝30°，分别以点A和点C为圆心，大于 $\frac{1}{2}$ AC的长为半径画弧，两弧相交于点M、N ，作直线MN ，交BC于点D ，连接AD ，则∠BAD的度数为（）

A、40° B、45° C、50° D、60°

查看试题解析
4. 联通公司推出两种手机收费方案．方案一：月租费36元，本地通话话费0.1元/分；方案二：不收月租费，本地通话费为0.6元/分．设小明的爸爸一个月通话时间为x分钟．小明爸爸一个月通话时间为多少时，选择方案一比方案二优惠（）

A、60分钟 B、70分钟 C、72分钟 D、80分钟

查看试题解析
5. 点P是等边三角形ABC所在平面上一点，若P和△ABC的三个顶点所组成的△PAB ， △PBC ， △PAC都是等腰三角形，则这样的点P的个数为（）

A、1 B、4 C、7 D、10

查看试题解析
6. 如图是跳棋盘，其中格点上的黑色点为棋子，剩余的格点上没有棋子．我们约定跳棋游戏的规则是：把跳棋棋子在棋盘内沿直线隔着棋子对称跳行，跳行一次称为一步．已知点A为已方一枚棋子，欲将棋子A跳进对方区域（阴影部分的格点），则跳行的最少步数为（）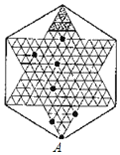

A、2 步 B、3 步 C、4 步 D、5 步

查看试题解析
7. “赵爽弦图”是由4个全等的直角三角形与中间的一个小正方形拼成的一个大正方形（如图所示）．若直角三角形的两条直角边的长分别是2和1，则图中阴影区域的面积与大正方形的面积之比为（）

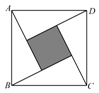A、 $\frac{1}{3}$ B、 $\frac{1}{4}$ C、 $\frac{1}{5}$ D、 $\frac{\sqrt{5}}{5}$

查看试题解析
8. 已知直线 $y = \frac{- (n + 1)}{n + 2} x + \frac{1}{n + 2}$ （n为正整数）与坐标轴围成的三角形的面积为S_n ，则S₁+S₂+S₃+⋯+S₂₀₁₂的值为（）

A、 $\frac{503}{2015}$ B、 $\frac{1006}{2015}$ C、 $\frac{1006}{2014}$ D、 $\frac{503}{2014}$

查看试题解析

二、填空题（共8小题，每小题3分，共24分）

9. 不等式组 ${\begin{matrix} x - 3 (x - 2) > 4 \\ \frac{2 x - 1}{5} \leq \frac{x + 1}{2} \end{matrix}$ 的解集为．

查看试题解析
10. 不等式x≤4的非负整数解是．

查看试题解析
11. 某班级从文化用品市场购买了签字笔和圆珠笔共15支，所付金额大于26元，但小于27元．已知签字笔每支2元，圆珠笔每支1.5元，则其中签字笔购买了支．

查看试题解析
12. 如图是由若干个粗细均匀的铁环最大限度地拉伸组成的链条．已知铁环粗1厘米，每个铁环长5厘米．设铁环间处于最大限度的拉伸状态．若要组成2米长的链条，则需要个铁环．

查看试题解析
13. 如图，O是边长为1的等边△ABC的中心，将AB ， BC ， CA分别绕点 A、点 B、点C顺时针旋转α（0°＜α＜180°），得到ABʹ，BCʹ，CAʹ，连接AʹBʹ，BʹCʹ，AʹCʹ，OAʹ，OBʹ．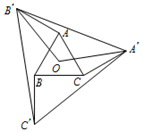

(1)、∠AʹOBʹ＝°；

(2)、当α＝°时，△AʹBʹCʹ的周长最大．

查看试题解析
14. 如图，在△ABC中，AB＝4，BC＝6，∠B＝60°，将△ABC沿射线BC的方向平移2个单位后，得到△AʹBʹCʹ，连接AʹC ，则△AʹBʹC的周长为．

查看试题解析
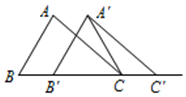15. 四边形ABCD的对角线AC，BD交于点O，点M，N，P，Q分别为边AB，BC，CD，DA的中点．有下列四个推断，
①对于任意四边形ABCD，四边形MNPQ都是平行四边形；

②若四边形ABCD是平行四边形，则MP与NQ交于点O；

③若四边形ABCD是矩形，则四边形MNPQ也是矩形；

④若四边形MNPQ是正方形，则四边形ABCD也一定是正方形．

所有正确推断的序号是．

查看试题解析
16. 如图，P是等边△ACB中的一个点，PA＝2， $P B = 2 \sqrt{3}$ ，PC＝4，则△ACB的边长是．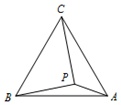

查看试题解析

三、解答题（共9小题；共72分）

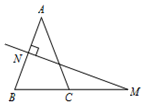
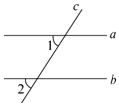
17. 已知：如图，直线a ， b被c所截，∠1，∠2是同位角，且∠1≠∠2．
求证：a不平行于b ．

查看试题解析
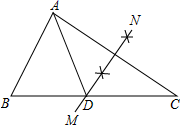
18. 如图1，把△ABC沿直线BC平移线段BC的长度，得到△ECD；如图2，以BC为轴，把△ABC沿BC翻折180°，可以得到△DBC；如图3，以点A为中心，把△ABC旋转180°，可以得到△AED ．像这样，其中一个三角形是由另一个三角形按平移、翻折、旋转等方法得到的，这种只改变位置，不改变形状、大小的图形变换，叫做三角形的全等变换．回答下列问题：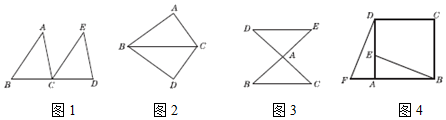

(1)、在图4中，可以使△ABE通过平移、翻折、旋转中的哪一种方法得到△ADF？

(2)、图中线段BE与DF相等吗？为什么？

查看试题解析
19. 若不等式组 ${\begin{cases} x < m + 1 ， \\ x > 2 m - 1 \end{cases}$ 无解，求m的取值范围．

查看试题解析
20. 在下列网格图中，每个小正方形的边长均为1个单位．在Rt△ABC中，∠C＝90°，AC＝3，BC＝4．

（1）试在图中做出△ABC以A为旋转中心，沿顺时针方向旋转90°后的图形△A₁B₁C₁；
（2）若点B的坐标为（﹣3，5），试在图中画出直角坐标系，并写出 A、C两点的坐标；
（3）根据（2）的坐标系作出与△ABC关于原点对称的图形△A₂B₂C₂ ，并写出B₂、C₂两点的坐标．

查看试题解析
21. 在等边△ABC中，点D ， E分别在边BC ， AC上，若CD＝2，过点D作DE∥AB ，过点E作EF⊥DE ，交BC的延长线于点F ，求EF的长．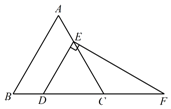

查看试题解析
22. 写出命题“如果一个角的两边与另一个角的两边分别垂直，那么这两个角相等”的逆命题，并判断原命题和逆命题的真假．若是假命题，请举出反例．

查看试题解析
23. 如图，FA⊥EC ，垂足为E ， ∠F＝40°，∠C＝20°，求∠FBC的度数．

查看试题解析
24. 解不等式组 ${\begin{matrix} 3 x - (x - 2) \geq 6 \\ x + 1 > \frac{4 x - 1}{3} \end{matrix}$ ．

查看试题解析
25. 如图，在△ABC中，AB＝AC ， AB的垂直平分线交AB于点N ，交BC的延长线于点M ，若∠BAC＝40°．

(1)、则∠NMB＝；

(2)、如果将题中∠BAC的度数改为70°，其余条件不变，那么∠NMB＝；

(3)、你发现有什么样的规律性？试证明；

(4)、若将题中的∠BAC改为钝角，你对这个规律性的认识是否需要加以修改？

查看试题解析