江苏省盐城市2021届九年级下学期数学期中考试试卷
试卷更新日期:2021-04-25 类型:期中考试
一、单选题
-
1. -2021的绝对值是( )A、2021 B、 C、- D、-20212. 下列运算正确的是 ( )A、x2·x3=x6 B、x2+x2=2x4 C、(-3a3)·(-5a5)=15a8 D、(-2x)2=-4x23. 人间四月芳菲始,踏青赏花正当时.记者从市文广旅局了解到,2021年清明小长假,我市统计的重点景区共接待游客186.5万人次,把186.5万用科学记数法表示为 ( )A、1.865×108 B、1.865×107 C、1.865×106 D、1.865×1024. 如图,直线a // b,点B在直线b上,且AB⊥BC,∠2=65°,则∠1的度数为 ( )
 A、65° B、45° C、35° D、25°5. 下列四个立体图形中,从正面看到的图形与其他三个不同的是( )A、
A、65° B、45° C、35° D、25°5. 下列四个立体图形中,从正面看到的图形与其他三个不同的是( )A、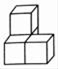 B、
B、 C、
C、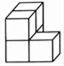 D、
D、 6. 某车间3月下旬生产零件的次品数如下(单位:个):0,2,0,2,3,0,2,3,1,2,则在这10天中该车间生产的零件的次品数的 ( )A、众数是0 B、中位数是2 C、平均数是2 D、极差是27. 若⊙O半径是2,点A在直线l上,且OA=2,则直线l与⊙O的位置关系是( )A、相切 B、相交 C、相离 D、相切或相交8. 如图,已知△ABC是等腰直角三角形,∠ABC=90°,A点坐标(-2,0),B点坐标为(1,1),点C在反比例函数 上,则k的值为( )
6. 某车间3月下旬生产零件的次品数如下(单位:个):0,2,0,2,3,0,2,3,1,2,则在这10天中该车间生产的零件的次品数的 ( )A、众数是0 B、中位数是2 C、平均数是2 D、极差是27. 若⊙O半径是2,点A在直线l上,且OA=2,则直线l与⊙O的位置关系是( )A、相切 B、相交 C、相离 D、相切或相交8. 如图,已知△ABC是等腰直角三角形,∠ABC=90°,A点坐标(-2,0),B点坐标为(1,1),点C在反比例函数 上,则k的值为( ) A、 B、 C、-4 D、-2
A、 B、 C、-4 D、-2二、填空题
-
9. 若二次根式 有意义,则x的取值范围是 .10. 分解因式:
11. 一个正多边形的每个外角为30°,则这个正多边形的边数为 .12. 在一次跳远训练中,甲、乙两人每人5次跳远的平均成绩都是2.38米,方差分别是 (米2), (米2),则在这次跳远训练中成绩比较稳定的是 .13. 已知实数m是关于x的方程-3x-1=0的一根,则代数式2-6m+2值为 .14. 如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹为120°,AB长为25cm,则纸扇外边缘弧BC长为cm. 15. 如图为甲、乙、丙三根笔直的钢管平行摆放在地面上的情形.已知乙有一部分只与甲重叠,其余部分只与丙重叠,甲没有与乙重叠的部分的长度为2m,丙没有与乙重叠的部分的长度为3m.若乙的长度最长且甲、乙的长度相差xm,乙、丙的长度相差ym,则乙的长度为m(用含有x、y的代数式表示).
15. 如图为甲、乙、丙三根笔直的钢管平行摆放在地面上的情形.已知乙有一部分只与甲重叠,其余部分只与丙重叠,甲没有与乙重叠的部分的长度为2m,丙没有与乙重叠的部分的长度为3m.若乙的长度最长且甲、乙的长度相差xm,乙、丙的长度相差ym,则乙的长度为m(用含有x、y的代数式表示). 16. 某园林单位要在一个绿化带内开挖一个△ABC的工作面,使得∠ACB=60°,CD是AB边上的高,且CD=6,则△ABC的面积最小值是 .
16. 某园林单位要在一个绿化带内开挖一个△ABC的工作面,使得∠ACB=60°,CD是AB边上的高,且CD=6,则△ABC的面积最小值是 .
三、解答题
-
17. 计算:18. 解不等式组:19. 先化简,再求值: ,其中 .20. 已知:在▱ABCD中,E、F是对角线AC上的两点,且AE=CF,对角线AC、BD交于点O.

求证:
(1)、△ABF≌△CDE;
(2)、BF//DE.
21. 如图,在平面直角坐标系中,直线l1:y=-x+3与过点A(-3,0)的直线l2交于点P(-1,m),与x轴交于点B.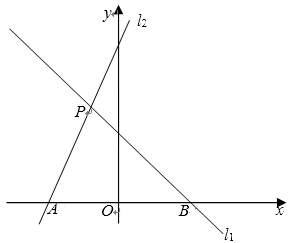 (1)、求直线l2的函数表达式;
(1)、求直线l2的函数表达式;
(2)、点M在直线l2上,MN//y轴,交直线l1于点N,若MN=AB,求点M的坐标.
22. 中国共产党,一个神圣而庄重的名字,今年我们伟大的党已经走过100年的光辉历程.为了庆祝中国共产党诞辰100周年,某校1000名学生准备在2021年7月1日“建党节”期间开展庆祝活动,对表达祝贺的方式,某班兴趣小组随机抽取了部分学生进行问卷调查,并将问卷调查的结果绘制成如下不完整的统计表:对党诞辰100周年祝贺的方式的统计表
方式
频数
百分比
诗歌朗诵
23
46%
歌唱
舞蹈
8%
其他
15
合计
100%
 (1)、本次问卷调查抽取的学生共有人,其中通过舞蹈表达祝贺的学生有人.(2)、分析上表的“频数”、“百分比”两列数据,补全扇形统计图横线上缺失的数据.(3)、根据抽样的结果,估计该校学生通过歌唱表达祝贺的约有多少人?23. 如图,已知△ABC中,AB=8,AC=6.
(1)、本次问卷调查抽取的学生共有人,其中通过舞蹈表达祝贺的学生有人.(2)、分析上表的“频数”、“百分比”两列数据,补全扇形统计图横线上缺失的数据.(3)、根据抽样的结果,估计该校学生通过歌唱表达祝贺的约有多少人?23. 如图,已知△ABC中,AB=8,AC=6. (1)、请用直尺(不带刻度)和圆规,按下列要求作图:
(1)、请用直尺(不带刻度)和圆规,按下列要求作图:①作∠CAB的角平分线交BC于点E;②作线段AE的垂直平分线分别交AB、AC于点D、F.
(2)、连接DE、EF,求四边形ADEF的周长.24. 疫情防控期间,任何人进入校园都必须测量体温,体温正常方可进校.现在学校需在东门、南门和西门分别增加一人测温,甲、乙、丙三人被随机增派到三个校门测温.小明每天走东门进校,小丽每天走西门进校.请用所学概率知识解决下列问题:(1)、写出甲、乙、丙被分配到三个校门测温的所有可能结果;(2)、小明、小丽两人中,进校时谁遇到甲的可能性大?请说明理由.25. 已知:一个⊙O与一个含有30°的Rt△CDE如图摆放,其中AB= ,CD=3,将Rt△CDE沿BA向左平移. (1)、当点C第一次落到⊙O上时,此时记为点 .求证: 与⊙O相切;(2)、当点C第二次落到⊙O上时,此时记为点 .求 、 、弧 围成的图形的面积.26. 小明为了能在4月份的体育加试中取得好成绩,每天进行掷实心球训练:当投掷实心球时会产生竖直向上的速度和水平向前的速度,研究表明:当这两个速度相等时,投掷距离最远.实心球在投掷的过程中的高度y与实心球出手后的时间t满足:y=-5t2+bt+2,水平距离x=at,a是出手后实心球水平向前的速度,b为出手后竖直向上的速度.
(1)、当点C第一次落到⊙O上时,此时记为点 .求证: 与⊙O相切;(2)、当点C第二次落到⊙O上时,此时记为点 .求 、 、弧 围成的图形的面积.26. 小明为了能在4月份的体育加试中取得好成绩,每天进行掷实心球训练:当投掷实心球时会产生竖直向上的速度和水平向前的速度,研究表明:当这两个速度相等时,投掷距离最远.实心球在投掷的过程中的高度y与实心球出手后的时间t满足:y=-5t2+bt+2,水平距离x=at,a是出手后实心球水平向前的速度,b为出手后竖直向上的速度. (1)、当 时,
(1)、当 时,①写出x与t的函数表达式为 , y与t的函数表达式为;
②结合所给的平面直角坐标系,求出y与x的函数表达式及此时投掷距离.
(2)、当a=b时,点O为投掷点,实心球落在圆心角为45°的∠AOB区域内时成绩有效,以实心球的落地点与投掷点O的距离为学生的投掷距离,已知落地点P在∠AOB区域内且到边界的距离PM= m,PN=6m,求出小明投掷的距离及实心球在此次投掷中的最高高度.27. 八年级下册,我们曾经探究过“一元一次方程、一元一次不等式与一次函数”之间的关系,学会了运用一次函数的图象可以解一元一次方程与一元一次不等式.例如:一次函数y=3x+2与x轴交点的横坐标是方程3x+2=0的解;一次函数y=3x+2在x轴上方部分图像的自变量取值范围是不等式3x+2>0的解集.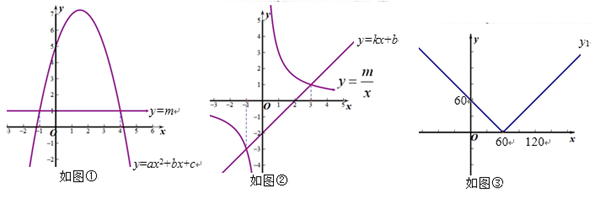
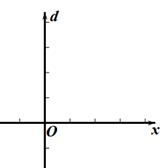 (1)、【类比解决】
(1)、【类比解决】利用图像解下列方程或不等式.
Ⅰ.如图①,方程ax2+bx+c-m=0的解为;
Ⅱ.如图②,不等式kx+b< 的解为 .
(2)、【拓展探究】已知函数y1=|60-x|,y2=|120-x|.
Ⅰ.利用分类思想,可将函数y1=|60-x|先转化为 ,然后分别画出y1=60-x的图像x≤60的部分和y1=x-60的图像x>60的部分,就可以得到函数y1=|60-x|的图像,如图③所示.请在图③所在的平面直角坐标系中直接画出y2=|120-x|的图像.
Ⅱ.已知min{m,n} =m(m≤n),例如:min{1,-2} =-2.若y=min{y1 , y2}的图像为W,请计算图像W与坐标轴围成图形的总面积.
(3)、【实际应用】有一条长为600米的步行道OA,A是垃圾投放点w1,若以O为原点,OA为x轴正半轴建立直角坐标系,设B(x,0),现要在步行道上建另一座垃圾投放点w2(t,0),点B与w1的距离为d1=|600-x|,点B与w2的距离为d2=|x-t|,d表示与B点距离最近的垃圾投放点的距离,即:d=min{d1,d2}.若可以通过函数d的图像与坐标轴围成的总面积来测算扔垃圾的便利程度,面积越小越便利.问:垃圾投放点w2建在何处才能比建在OA中点时更加便利?