河南省平顶山市2020-2021学年七年级下学期数学期中考试试卷
试卷更新日期:2021-04-25 类型:期中考试
一、选择题(本大题共10小题,共30分)
-
1. 下列运算正确的是( )A、a2+a2=a4 B、(-b2)3=-b6 C、2x•2x2=2x3 D、(m-n)2=m2-n22. 某种原子的直径为0.0000000002米,用科学记数法表示为( )A、0.2×10﹣10 B、2×10﹣10 C、1×10﹣10 D、0.1×10﹣103. 若ax=3,ay=2,则a2x+y等于( )A、6 B、7 C、8 D、184. 如果 是完全平方式,那么k的值是( )A、-12 B、6 C、±12 D、±65. 下列图形中, 1和 2是同位角的是( )
A、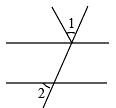 B、
B、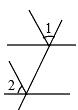 C、
C、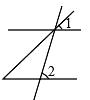 D、
D、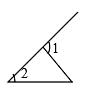 6. 如图,直线a∥b,若∠1=50°,∠3=95°,则∠2的度数为( )
6. 如图,直线a∥b,若∠1=50°,∠3=95°,则∠2的度数为( )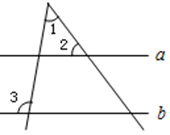 A、35° B、40° C、45° D、55°7. 将一直角三角板与两边平行的纸条如图放置.若∠1=60°,则∠2的度数为( )
A、35° B、40° C、45° D、55°7. 将一直角三角板与两边平行的纸条如图放置.若∠1=60°,则∠2的度数为( ) A、60° B、45° C、50° D、30°8. 如图,点E在BC的延长线上,下列条件不能判断AB∥CD的是( )
A、60° B、45° C、50° D、30°8. 如图,点E在BC的延长线上,下列条件不能判断AB∥CD的是( )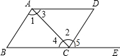 A、∠1=∠2 B、∠3=∠4 C、∠5=∠B D、∠B+∠BCD=180°9. 把一张对面互相平行的纸条折成如图所示那样,EF是折痕,若∠EFB=32°则下列结论正确的有( )
A、∠1=∠2 B、∠3=∠4 C、∠5=∠B D、∠B+∠BCD=180°9. 把一张对面互相平行的纸条折成如图所示那样,EF是折痕,若∠EFB=32°则下列结论正确的有( )
( 1 )∠C′EF=32°(2)∠AEC=116°(3)∠BGE=64°(4)∠BFD=116°.
A、1个 B、2个 C、3个 D、410. 两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,在探究筝形的性质时,得到如下结论:①△ABD≌△CBD;②AC⊥BD;③四边形ABCD的面积= AC·BD.其中正确的结论有( )
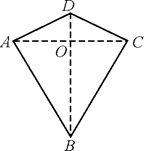 A、0个 B、1个 C、2个 D、3个
A、0个 B、1个 C、2个 D、3个二、填空题(本大题共5小题,共15分)
-
11. 已知 , ,则xy的值为 .12. 如图,一个上下边平行的纸条按如图所示方法折叠一下,则 度 .
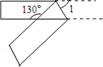 13. 已知直线 ,将一个含45°角的直角三角板ABC按如图所示方式放置,其中斜边BC与直线n交于点D.若 ,则 的度数为.
13. 已知直线 ,将一个含45°角的直角三角板ABC按如图所示方式放置,其中斜边BC与直线n交于点D.若 ,则 的度数为. 14. 如图,知 ,则 .
14. 如图,知 ,则 . 15. 如图,点 , , 在同一条直线上, ,请你只添加一个条件,使得 .你添加的条件是 . (要求:不再添加辅助线,只需填一个答案即可)
15. 如图,点 , , 在同一条直线上, ,请你只添加一个条件,使得 .你添加的条件是 . (要求:不再添加辅助线,只需填一个答案即可)
三、计算题(本大题共2小题,共30分)
-
16.(1)、2y•(-2xy3)(2)、(2x+y)2-(2x+3y)(2x-3y)(3)、22021×(0.5)2020(4)、﹣32+|﹣3|+(﹣1)2016×(π﹣3)0﹣( )﹣117. 化简并求值:
[(x+2y)2-(x+y)(3x-y)-5y2]÷2x,其中x=-2,y= .
四、解答题(本大题共5小题,共30.0分)
-
18. 已知: 及边 上一点 .求作: ,使得 = .

要求:
(1)、尺规作图,保留作图痕迹,不写作法;(2)、请你写出作图的依据.19. 如图,直线AD分与直线BE、直线CE、直线CF、直线BF相交于点A、G、D、H,且∠1=∠2,∠B=∠C.请问:AB∥CD吗?试说明理由。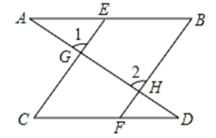 20. 如图,EF∥AD,∠1=∠2,∠BAC=80°.求∠AGD的度数.
20. 如图,EF∥AD,∠1=∠2,∠BAC=80°.求∠AGD的度数.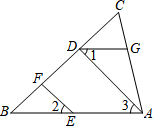 21.(1)、如图,在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P.
21.(1)、如图,在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P.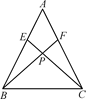
求证:PB=PC.
(2)、补充完成下列推理过程:如图,在△ABC中,AB=AC,点D,E分别是BC,AC上的点,且BD=CE,连接AD,DE,若∠ADE=∠B.
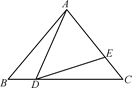
求证:AD=DE.
证明:∵AB=AC,∴∠B=∠C(▲ ).
∵∠ADC=∠B+∠_▲_ (_▲),且∠ADE=∠B,
∴∠ADC=∠ADE+∠_▲_.又∵∠ADC=∠ADE+∠CDE,∴∠BAD=∠CDE.
在△BAD和△CDE中,
∴△BAD≌△CDE(__▲).∴AD=DE(_▲).
22. 如图,AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在的直线交于点E,∠ADC=70°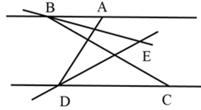
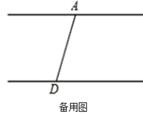 (1)、求∠EDC的度数;(2)、若∠ABC=30°,求∠BED的度数;(3)、将线段BC沿DC方向移动,使得点B在点A的右侧,其他条件不变,若∠ABC=n°,请直接写出∠BED的度数?(用含n的代数式表示)
(1)、求∠EDC的度数;(2)、若∠ABC=30°,求∠BED的度数;(3)、将线段BC沿DC方向移动,使得点B在点A的右侧,其他条件不变,若∠ABC=n°,请直接写出∠BED的度数?(用含n的代数式表示)