陕西省西安市未央区2020-2021学年七年级上学期数学期末考试试卷
试卷更新日期:2021-04-25 类型:期末考试
一、单选题
-
1. 2020年天猫“双十一”全球狂欢季实时成交额突破4982亿元,创造新历史.将数据4982亿用科学记数法表示为( )A、 4982×108 B、4.982×1011 C、49.82×1011 D、4.982×10102. 下列调查中,最适合采用抽样调查(抽查)的是( )A、调查“神舟十一号飞船”各部分零件情况 B、调查旅客随身携带的违禁物品 C、调查全国观众对中央一台“新闻联播”的收视情况 D、调查某中学七年级某班学生数学寒假作业完成情况3. 如图,一个正方体有盖盒子(可密封)里装入六分之一高度的水,改变正方体盒子的放置方式,下列选项中不是盒子里的水能形成的几何体是( )
 A、正方体 B、长方体 C、三棱柱 D、三棱锥4. 下面的说法正确的是( )A、单项式 的次数是2次 B、 的系数是3 C、 与 是同类项 D、 不是多项式5. 如图,点A,B,C顺次在直线上,点M是线段AC的中点,点N是线段BC的中点,已知AB=16cm,MN=( )
A、正方体 B、长方体 C、三棱柱 D、三棱锥4. 下面的说法正确的是( )A、单项式 的次数是2次 B、 的系数是3 C、 与 是同类项 D、 不是多项式5. 如图,点A,B,C顺次在直线上,点M是线段AC的中点,点N是线段BC的中点,已知AB=16cm,MN=( )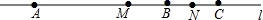 A、6cm B、8cm C、9cm D、10cm6. 下列生活实例中,数学原理解释错误的一项是( )A、从一条河向一个村庄引一条最短的水渠,其中数学原理是:在同一平面内,过一点有且只有一条直线垂直于已知直线 B、两个村庄之间修一条最短的公路,其中的数学原理是:两点之间线段最短 C、把一个木条固定到墙上需要两颗钉子,其中的数学原理是:两点确定一条直线 D、从一个货站向一条高速路修一条最短的公路,其中的数学原理是:连结直线外一点与直线上各点的所有线段中,垂线段最短7. 某商品的价格标签已丢失,售货员只知道它的进价为80元,打七折售出后,仍可获利5%,你认为标签上的价格为( )元.A、110 B、120 C、130 D、1408. 如图,在下面四种用相同的正方体储物箱堆放在一起的形态中,从正面看到的和从左面看到的图形不相同的是( )A、
A、6cm B、8cm C、9cm D、10cm6. 下列生活实例中,数学原理解释错误的一项是( )A、从一条河向一个村庄引一条最短的水渠,其中数学原理是:在同一平面内,过一点有且只有一条直线垂直于已知直线 B、两个村庄之间修一条最短的公路,其中的数学原理是:两点之间线段最短 C、把一个木条固定到墙上需要两颗钉子,其中的数学原理是:两点确定一条直线 D、从一个货站向一条高速路修一条最短的公路,其中的数学原理是:连结直线外一点与直线上各点的所有线段中,垂线段最短7. 某商品的价格标签已丢失,售货员只知道它的进价为80元,打七折售出后,仍可获利5%,你认为标签上的价格为( )元.A、110 B、120 C、130 D、1408. 如图,在下面四种用相同的正方体储物箱堆放在一起的形态中,从正面看到的和从左面看到的图形不相同的是( )A、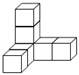 B、
B、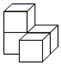 C、
C、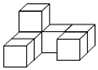 D、
D、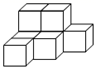 9. 中国快递越来越“科技范儿”,分拣机器人、大数据AI调度等智能装备系统让分拣效率大大提升.某分拣仓库采用智能分拣系统计划平均每天分拣20万件包裹,但实际每天分拣量与计划相比有出入,超过计划量记为正,未达计划量记为负,下面是该仓库10月份第一周分拣包裹的情况(单位:万件):+5,﹣1,﹣3,+6,﹣1,+4,﹣8,该仓库本周实际分拣包裹一共是( )A、138万件 B、140万件 C、141万件 D、142万件10. 下面是用黑色棋子摆成的美丽图案,按照这样的规律摆下去,第10个这样的图案需要黑色棋子的个数为( )
9. 中国快递越来越“科技范儿”,分拣机器人、大数据AI调度等智能装备系统让分拣效率大大提升.某分拣仓库采用智能分拣系统计划平均每天分拣20万件包裹,但实际每天分拣量与计划相比有出入,超过计划量记为正,未达计划量记为负,下面是该仓库10月份第一周分拣包裹的情况(单位:万件):+5,﹣1,﹣3,+6,﹣1,+4,﹣8,该仓库本周实际分拣包裹一共是( )A、138万件 B、140万件 C、141万件 D、142万件10. 下面是用黑色棋子摆成的美丽图案,按照这样的规律摆下去,第10个这样的图案需要黑色棋子的个数为( )


 A、148 B、152 C、174 D、202
A、148 B、152 C、174 D、202二、填空题
-
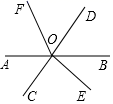
11. 在1, ,0, 四个数中,最小的数是.12. 如图,直线AB、CD相交于点O,∠COE是直角,OF平分∠AOD,若∠BOE=42°,则∠AOF的度数是.
 13.
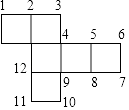
13.如图是一个正方体纸盒的展开图,当折成纸盒时,与数11重合的数是 .
 14. 一组“数值转换机”按下面的程序计算,如果输入的数是30,则输出的结果为56,要使输出的结果为76,则输入的最小正整数是.
14. 一组“数值转换机”按下面的程序计算,如果输入的数是30,则输出的结果为56,要使输出的结果为76,则输入的最小正整数是.
三、解答题
-
15. 计算﹣23+|5﹣14|+25×(﹣ ).16. 先化简,再求值:2(3xy-x2)-3(xy-2x2)-xy,其中x=- ,y=3.17. 解方程: .18. 如图,平面上有A、B、C、D四个点,根据下列语句画图.
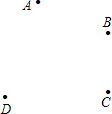
( 1 )画直线AB,作射线AD,画线段BC;
( 2 )连接DC,并将线段DC延长至E,使DE=2DC.
19. 已知a、b互为相反数且a≠0,c、d互为倒数,|m|是最小的正整数,求2m+ -cd的值.20. 2020年2月,西安市积极响应国家“停课不停学”的号召,推行“网课教学”.为了解学生对网上在线学习效果的满意度,某校设置了:非常满意、满意、基本满意、不满意四个选项.随机抽查了部分学生,要求每名学生都只选其中的一项,并将抽查结果绘制成如图统计图(不完整).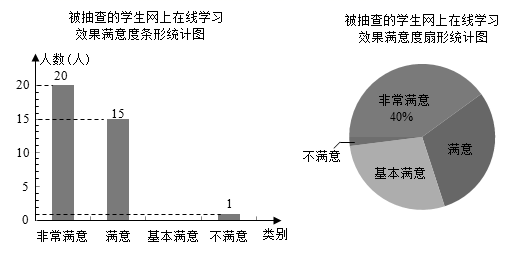
请根据图中信息解答下列问题:
(1)、求被抽查的学生人数,并补全条形统计图;(温馨提示:请画在答题卡相对应的图上)(2)、求扇形统计图中表示“满意”的扇形的圆心角度数;(3)、若该校共有3800名学生参与网上在线学习,根据抽查结果,试估计该校对学习效果的满意度是“非常满意”或“满意”的学生共有多少人?21. 如图,OB、OC是 内部的两条射线, OM平分 ,ON平分 .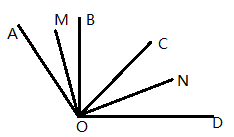 (1)、若 ,求 的度数;(2)、若 ,求 的度数(用含x的代数式表示)22. 开学发新书,两摞规格相同的数学新课本如图所示,整齐地叠放在课桌上,请根据图中所给的数据信息,解答下列问题:
(1)、若 ,求 的度数;(2)、若 ,求 的度数(用含x的代数式表示)22. 开学发新书,两摞规格相同的数学新课本如图所示,整齐地叠放在课桌上,请根据图中所给的数据信息,解答下列问题: (1)、每本数学新课本的厚度为厘米;(2)、当数学新课本数为x(本)时,请直接写出同样叠放在桌面上的一摞数学新课本最上面高出地面的距离(用含x的代数式表示);(3)、如果有一个班级的学生每人要领取1本数学新课本,全班的数学新课本放在桌面上,班级中 的学生领取后,桌上剩余的数学新课本整齐地摆放成一摞,课本最上面高出地面的距离为96.8厘米,你能从中知道该班学生的人数吗?请说出理由.23. 如图,有两条线段,AB=2(单位长度),CD=1(单位长度)在数轴上,点A在数轴上表示的数是﹣12,点D在数轴上表示的数是15.
(1)、每本数学新课本的厚度为厘米;(2)、当数学新课本数为x(本)时,请直接写出同样叠放在桌面上的一摞数学新课本最上面高出地面的距离(用含x的代数式表示);(3)、如果有一个班级的学生每人要领取1本数学新课本,全班的数学新课本放在桌面上,班级中 的学生领取后,桌上剩余的数学新课本整齐地摆放成一摞,课本最上面高出地面的距离为96.8厘米,你能从中知道该班学生的人数吗?请说出理由.23. 如图,有两条线段,AB=2(单位长度),CD=1(单位长度)在数轴上,点A在数轴上表示的数是﹣12,点D在数轴上表示的数是15. (1)、点B在数轴上表示的数是 , 点C在数轴上表示的数是 , 线段BC的长=;(2)、若线段AB以1个单位长度/秒的速度向右匀速运动,同时线段CD以2个单位长度/秒的速度向左匀速运动.当点B与C重合时,点B与点C在数轴上表示的数是多少?(3)、若线段AB以1个单位长度/秒的速度向左匀速运动,同时线段CD以2个单位长度/秒的速度也向左匀速运动.设运动时间为t秒,当0<t<24时,M为AC中点,N为BD中点,则线段MN的长为多少?
(1)、点B在数轴上表示的数是 , 点C在数轴上表示的数是 , 线段BC的长=;(2)、若线段AB以1个单位长度/秒的速度向右匀速运动,同时线段CD以2个单位长度/秒的速度向左匀速运动.当点B与C重合时,点B与点C在数轴上表示的数是多少?(3)、若线段AB以1个单位长度/秒的速度向左匀速运动,同时线段CD以2个单位长度/秒的速度也向左匀速运动.设运动时间为t秒,当0<t<24时,M为AC中点,N为BD中点,则线段MN的长为多少?