湘教版备考2021年中考数学二轮复习专题8轴对称、旋转与中心对称
试卷更新日期:2021-04-25 类型:二轮复习
一、单选题
-
1. 如图,△ABC和△A′B′C′关于直线L对称,下列结论中正确的有( )
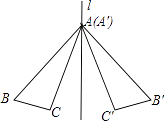
⑴△ABC≌△A′B′C′
⑵∠BAC=∠B′A′C′
⑶直线L垂直平分CC′
⑷直线BC和B′C′的交点不一定在直线L上.
A、4个 B、3个 C、2个 D、1个2. 如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有( ) A、1种 B、2种 C、3种 D、4种3. 下列语句中,正确的个数有( )
A、1种 B、2种 C、3种 D、4种3. 下列语句中,正确的个数有( )①两个关于某直线对称的图形是全等的
②两个图形关于某直线对称,对称点一定在该直线的两旁
③两个成轴对称的图形的对应点连线的垂直平分线,就是它们的对称轴
④平面内两个全等的图形一定关于某直线对称.
A、1个 B、2个 C、3个 D、4个4. 如图,图中显示的是从镜子中看到背后墙上的电子钟读数,由此你可以推断这时的实际时间是( ) A、 B、 C、 D、5. 将一个正方形纸片按如图1、图2依次对折后,再按如图3打出一个心形小孔,则展开铺平后的图案是( )
A、 B、 C、 D、5. 将一个正方形纸片按如图1、图2依次对折后,再按如图3打出一个心形小孔,则展开铺平后的图案是( )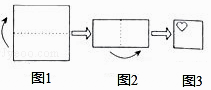 A、
A、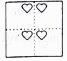 B、
B、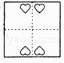 C、
C、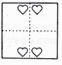 D、
D、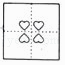 6. 如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为( )
6. 如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为( ) A、 B、2 C、2 D、7. 如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
A、 B、2 C、2 D、7. 如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )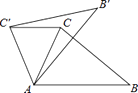 A、35° B、40° C、50° D、65.8. 下列图形中,是中心对称图形的是( )A、
A、35° B、40° C、50° D、65.8. 下列图形中,是中心对称图形的是( )A、 B、
B、 C、
C、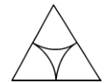 D、
D、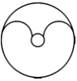 9. 如图,∠AOB=30°,∠AOB 内有一定点 P,且 OP=12,在 OA 上有一动点 Q,OB 上有 一动点 R。若△PQR 周长最小,则最小周长是( )
9. 如图,∠AOB=30°,∠AOB 内有一定点 P,且 OP=12,在 OA 上有一动点 Q,OB 上有 一动点 R。若△PQR 周长最小,则最小周长是( )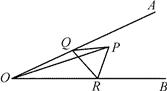 A、6 B、12 C、16 D、2010. 如图△ABC与△CDE都是等边三角形,且∠EBD=65°,则∠AEB的度数是( )
A、6 B、12 C、16 D、2010. 如图△ABC与△CDE都是等边三角形,且∠EBD=65°,则∠AEB的度数是( )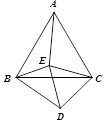 A、115° B、120° C、125° D、130°11. 如图,在4× 4的网格纸中,△ABC的三个顶点都在格点上.现要在这张网格纸中找出一格点作为旋转中心,绕着这个中心旋转后的三角形的顶点也在格点上,若旋转前后的两个三角形构成中心对称图形,那么满足条件的旋转中心有( )
A、115° B、120° C、125° D、130°11. 如图,在4× 4的网格纸中,△ABC的三个顶点都在格点上.现要在这张网格纸中找出一格点作为旋转中心,绕着这个中心旋转后的三角形的顶点也在格点上,若旋转前后的两个三角形构成中心对称图形,那么满足条件的旋转中心有( )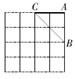 A、2个 B、3个 C、4个 D、20个
A、2个 B、3个 C、4个 D、20个二、填空题
-
12. 如图, 是 的边 上的中线,将线段 绕点D顺时针旋转 后,点A的对应点E恰好落在 边上,若 , ,则 的长为.
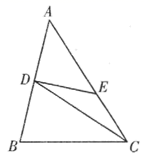 13. 如图,把一张长方形的纸沿对角线折叠,若 ,则 .
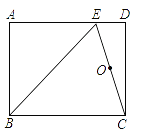
13. 如图,把一张长方形的纸沿对角线折叠,若 ,则 .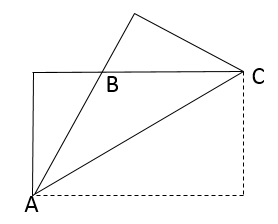 14. 如图,正方形ABCD旋转后能与正方形CDEF重合,那么点A,B,C,D中,可以作为旋转中心的有个.
14. 如图,正方形ABCD旋转后能与正方形CDEF重合,那么点A,B,C,D中,可以作为旋转中心的有个.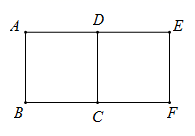 15. 如图,在 的正方形的网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形.图中的 为格点三角形,在图中最多能画出个不同的格点三角形与 成轴对称.
15. 如图,在 的正方形的网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形.图中的 为格点三角形,在图中最多能画出个不同的格点三角形与 成轴对称. 16. 如图,已知正方形ABCD的边长是4,点E是AB边上一动点,连接CE,过点B作BG⊥CE于点G,点P是AB边上另一动点,则PD+PG的最小值为 .
16. 如图,已知正方形ABCD的边长是4,点E是AB边上一动点,连接CE,过点B作BG⊥CE于点G,点P是AB边上另一动点,则PD+PG的最小值为 .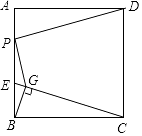 17. 如图,矩形ABCD中,AB=12cm,BC=24cm,如果将该矩形沿对角线BD折叠,那么图中阴影部分的面积 .
17. 如图,矩形ABCD中,AB=12cm,BC=24cm,如果将该矩形沿对角线BD折叠,那么图中阴影部分的面积 .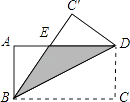 18. 如图,将n个边长都为1cm的正方形按如图所示摆放,点A1, A2,…,An分别是正方形的中心,则n个正方形重叠形成的重叠部分的面积和为
18. 如图,将n个边长都为1cm的正方形按如图所示摆放,点A1, A2,…,An分别是正方形的中心,则n个正方形重叠形成的重叠部分的面积和为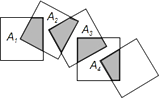 19. 如图,在 中,∠C=90°,AC=3,BC=4,点 是 中点,将 绕点 旋转得 ,则在旋转过程中点 两点间的最大距离是 .
19. 如图,在 中,∠C=90°,AC=3,BC=4,点 是 中点,将 绕点 旋转得 ,则在旋转过程中点 两点间的最大距离是 . 20. 下列图形中,①等腰三角形;②平行四边形;③等腰梯形;④圆;⑤正六边形;⑥菱形;⑦正五边形,是中心对称图形的有(填序号)
20. 下列图形中,①等腰三角形;②平行四边形;③等腰梯形;④圆;⑤正六边形;⑥菱形;⑦正五边形,是中心对称图形的有(填序号)三、解答题
-
21. 如图,A点是牧马营地.每天牧马人都要从营地出发,赶着马群先到河边饮水,再到草地吃草,然后回到营地.问:怎样的放牧路线,路程最短?
 22. 如图,△ABC中,∠BAC=120o , 以BC为边向外作等边△BCD,把△ABD绕着D点按顺时针方向旋转60o后到△ECD的位置。若AB=6,AC=4,求∠BAD的度数和AD的长.
22. 如图,△ABC中,∠BAC=120o , 以BC为边向外作等边△BCD,把△ABD绕着D点按顺时针方向旋转60o后到△ECD的位置。若AB=6,AC=4,求∠BAD的度数和AD的长.
四、作图题
-
23.
在 的方格中,△ABC的三个顶点都在格点上.
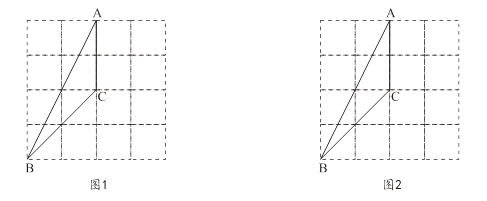 (1)、在图1中画出与△ABC成轴对称且与△ABC有公共边的格点三角形(画出一个即可);(2)、将图2中的△ABC绕着点C按顺时针方向旋转90°,画出经旋转后的三角形.24. 有一个养鱼专业户,在如图所示地形的两个池塘里养鱼,他每天早上要从住处P分别前往两个池塘投放鱼食,试问他怎样走才能以最短距离回到住地?(请用尺规作图,保留作图痕迹,不写做法)
(1)、在图1中画出与△ABC成轴对称且与△ABC有公共边的格点三角形(画出一个即可);(2)、将图2中的△ABC绕着点C按顺时针方向旋转90°,画出经旋转后的三角形.24. 有一个养鱼专业户,在如图所示地形的两个池塘里养鱼,他每天早上要从住处P分别前往两个池塘投放鱼食,试问他怎样走才能以最短距离回到住地?(请用尺规作图,保留作图痕迹,不写做法)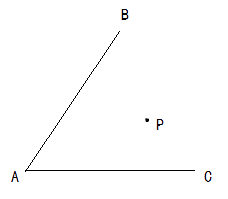 25. 由16个边长相等的小正方形组成的图形如图所示,请你用一条割线(可以是折线)将它分割成两个图形,使之关于某一点成中心对称,要求给出两种不同的方法.
25. 由16个边长相等的小正方形组成的图形如图所示,请你用一条割线(可以是折线)将它分割成两个图形,使之关于某一点成中心对称,要求给出两种不同的方法.
五、综合题
-
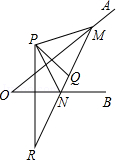
26. 如图,∠AOB=30°,点P是∠AOB内一点,PO=8,在∠AOB的两边分别有点R、Q(均不同于O),求△PQR周长的最小值.
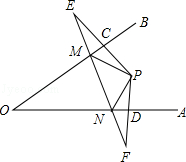
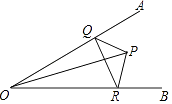 27. 如图,点P是∠AOB外的一点,点Q与P关于OA对称,点R与P关于OB对称,直线QR分别交OA,OB于点M,N,若PM=PN=3,MN=4,求线段QR的长.
27. 如图,点P是∠AOB外的一点,点Q与P关于OA对称,点R与P关于OB对称,直线QR分别交OA,OB于点M,N,若PM=PN=3,MN=4,求线段QR的长.