湘教版备考2021年中考数学二轮复习专题7相交线与平行线

试卷更新日期：2021-04-24 类型：二轮复习

进入出卷网下载

一、单选题

1. 下列语句：
①不相交的两条直线叫平行线
②在同一平面内，两条直线的位置关系只有两种：相交和平行
③如果线段AB和线段CD不相交，那么直线AB和直线CD平行
④如果两条直线都和第三条直线平行，那么这两条直线平行
⑤过一点有且只有一条直线与已知直线平行
正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
2. 两条直线最多有1个交点，三条直线最多有3个交点，四条直线最多有6个交点，那么六条直线最多有（）

A、21个交点 B、18个交点 C、15个交点 D、10个交点

查看试题解析
3. 已知n（n≥3，且n为整数）条直线中只有两条直线平行，且任何三条直线都不交于同一个点．如图，当n=3时，共有2个交点；当n=4时，共有5个交点；当n=5时，共有9个交点；…依此规律，当共有交点个数为27时，则n的值为（）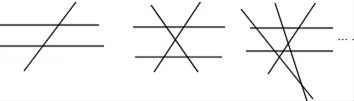

A、6 B、7 C、8 D、9

查看试题解析
4. 如图，AB∥EF∥CD，∠ABC=46°，∠CEF=154°，则∠BCE 等于（）

A、16° B、20° C、23° D、26°

查看试题解析
5. 如图，下列条件：①∠1＝∠3；②∠2＝∠3；③∠4＝∠5；④∠2＋∠4＝180°中，能判断直线l₁∥l₂的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 如图，∠BCD＝95°，AB∥DE，则∠α与∠β满足（）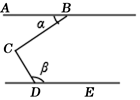

A、∠α+∠β＝95° B、∠β﹣∠α＝95° C、∠α+∠β＝85° D、∠β﹣∠α＝85°

查看试题解析
7. 如图所示，把长方形ABCD的斜对角AC等分成6段，以每一段为斜对角线作6个小长方形，若AB＝1，BC＝2.5，则6个小长方形的周长之和等于（）

A、3.5 B、3 C、7 D、5

查看试题解析
8. 如图，矩形 $A B C D$ 中， $A B = 4$ ， $A D = 2$ ， $E$ 为 $A B$ 的中点， $F$ 为 $E C$ 上一动点， $P$ 为 $D F$ 中点，连接 $P B$ ，则 $P B$ 的最小值是（）

A、2 B、4 C、 $\sqrt{2}$ D、 $2 \sqrt{2}$

查看试题解析
9. 如图，AB∥CD，点E为AB上方一点，FB，HG分别为∠EFG，∠EHD的角平分线，若∠E+2∠G＝150°，则∠EFG的度数为（）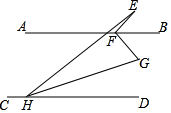

A、90° B、95° C、100° D、150°

查看试题解析

二、填空题

10. 如图，EF∥AD，∠1=∠2， ∠BAC=70°，将求∠AGD的过程填空完整。
解：∵EF∥AD
∴∠2=（）
又∵∠1=∠2
∴∠1=∠3（）
∴AB∥（）
∵∠BAC+=180°（）
∵∠BAC=70° ∴∠AGD=。

查看试题解析
11. “浏阳河弯过九道弯，五十里水路到湘江．”如图所示，某段河水流经B ， C ， D三点拐弯后与原来流向相同，若∠ABC＝120°，∠BCD＝80°，则∠EDC＝．

查看试题解析
12. 如图所示， $A C ⊥ B C$ 于C ， $A D ⊥ C D$ 于D ， $A B = 5 ，$ $A D = 3$ ，则AC的取值范围是.

查看试题解析
13. 如图，已知直线m//n，A，B 为直线m上的两点，C，P 为直线n上的两点．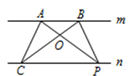

(1)、请写出图中面积相等的各对三角形：；

(2)、如果A，B，C 为三个定点，点P 在直线n上移动，那么，无论P 点移动到任何位置，总有．
理由是：．

查看试题解析
14. 如图，已知∠1=∠2，∠B=40°，则∠3= ．

查看试题解析

三、解答题

15. 将一副直角三角板如图放置，已知AE∥BC，求∠AFD的度数．

查看试题解析
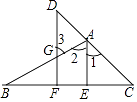
16.
如图，已知D是CA延长线上一点，AE⊥BC，DF⊥BC，垂足分别为E、F，DF与AB相交于点G，且∠D=∠3，请说明AE平分∠BAC．

查看试题解析
17.
如图，在6×4的正方形网格中，点A、B、C、D、E、F都在格点上．连接点A、B得线段AB．

(1)、连接C、D、E、F中的任意两点，共可得　条线段，在图中画出来；

(2)、在（1）中所连得的线段中，与AB平行的线段是　；

(3)、用三角尺或量角器度量、检验，AB及（1）中所连得的线段中，互相垂直的线段有几对？（请用“⊥”表示出来）　．

查看试题解析
18.
将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起（其中，∠A=60°，∠D=30°；∠E=∠B=45°）：

(1)、若∠DCE=45°，则∠ACB的度数为

(2)、若∠ACB=140°，求∠DCE的度数

(3)、由（1）猜想∠ACB与∠DCE的数量关系，并说明理由．

(4)、当∠ACE＜180°且点E在直线AC的上方时，这两块三角尺是否存在一组边互相平行？若存在，请直接写出∠ACE角度所有可能的值（不必说明理由）；若不存在，请说明理由．

查看试题解析

四、作图题

19. 如图，已知直线l ，点A是直线l外一点，用尺规作l的垂线，使它经过点A（请保留作图痕迹，不写做法）。

查看试题解析
20.
在如图所示的方格纸上过点P画直线AB的平行线，过点P作PM⊥AB于点M．

查看试题解析

五、综合题

21.
如图1，AB∥CD，EOF是直线AB、CD间的一条折线．

(1)、试证明：∠O=∠BEO+∠DFO．

(2)、如果将折一次改为折二次，如图2，则∠BEO、∠O、∠P、∠PEC之间会满足怎样的数量关系，证明你的结论．

查看试题解析
22. 如图，点E在直线BH、DC之间，点A为BH上一点，且AE⊥CE， $∠ D C E - ∠ H A E = 90 °$ .

(1)、求证：BH∥CD；

(2)、如图：直线AF交DC于F，AM平分∠EAF，AN平分∠BAE. 试探究∠MAN，∠AFG的数量关系.

查看试题解析
23. 平面上有7条不同的直线，如果其中任何三条直线都不共点．

(1)、请画出满足上述条件的一个图形，并数出图形中各直线之间的交点个数；

(2)、请再画出各直线之间的交点个数不同的图形（至少两个）；

(3)、你能否画出各直线之间的交点个数为n的图形，其中n分别为6，21，15？

(4)、请尽可能多地画出各直线之间的交点个数不同的图形，从中你能发现什么规律？

查看试题解析
24. 学习完平行线的性质与判定之后，我们发现借助构造平行线的方法可以帮我们解决许多问题．

(1)、小明遇到了下面的问题：如图 $l_{1} ∥ l_{2}$ ，点P在 $l_{1}$ 、 $l_{2}$ 内部，探究 $∠ A$ ， $∠ APB$ ， $∠ B$ 的关系．小明过点P作 $l_{1}$ 的平行线，可得到 $∠ APB$ ， $∠ A$ ， $∠ B$ 之间的数量关系是： $∠ APB =$ .

(2)、如图2，若 $AC ∥ BD$ ，点P在AC、BD外部， $∠ A$ ， $∠ B$ ， $∠ APB$ 的数量关系如何？为此，小明进行了下面不完整的推理证明.请将这个证明过程补充完整，并在括号内填上依据．过点P作 $PE ∥ AC$ ．
∴ $∠ A = ∠ APE$ （）

∵ $AC ∥ BD$ ，

∴ $BD ∥ PE$ （）

∴ $∠ B = ∠ BPE$ ，

∵ $∠ APB = ∠ BPE - ∠ APE$ ，

∴ $∠ APB =$ .（）

(3)、随着以后的学习你还会发现平行线的许多用途．如图3，在小学中我们已知道，三角形ABC中， $∠ A + ∠ B + ∠ C = 180^{°}$ ．试构造平行线说明理由.

查看试题解析