高考必做大题05：热力学综合
试卷更新日期：2021-04-24 类型：三轮冲刺
一、计算题
-
1. 如图所示，将横截面积S=100cm2、容积为V=5L，开口向上的导热良好的气缸，置于t1=－13℃的环境中。用厚度不计的轻质活塞将体积为V1=4L的理想气体封闭在气缸中，气缸底部有一个单向阀门N。外界大气压强p0=1.0×105Pa，重力加速g=10m/s2 ， 不计一切摩擦。求：
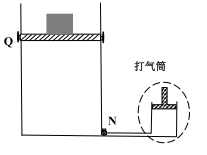
(i)将活塞用卡销Q锁定，用打气筒通过阀门N给气缸充气，每次可将体积V0=100mL，压强为p0的理想气体全部打入气缸中，则打气多少次，才能使其内部压强达到1.2p0；
(ii)当气缸内气体压强达到1.2p0时，停止打气，关闭阀门N，将质量为m=20kg的物体放在活塞上，然后拔掉卡销Q，则环境温度为多少摄氏度时，活塞恰好不脱离气缸。
2. 如图所示，固定的气缸Ⅰ和气缸Ⅱ的活塞用劲度系数为k＝200N/cm的轻质弹簧相连，两活塞横截面积的大小满足S1＝2S2 ， 其中S2＝20cm2 ． 两气缸均用导热材料制成，内壁光滑，两活塞可自由移动。初始时两活塞静止不动，与气缸底部的距离均为L0＝30cm，环境温度为T0＝300K，外界大气压强为 ，弹簧处于原长。现只给气缸Ⅰ缓慢加热，使气缸Ⅱ的活塞缓慢移动了15cm。已知活塞没有到达气缸口，弹簧能保持水平，气缸内气体可视为理想气体。求此时：
（a）弹簧的形变量；
（b）气缸Ⅰ内气体的温度。
3. 如图所示，一竖直放置的导热性能良好的汽缸上端开口，汽缸壁内设有卡口，卡口到缸底间距离为10cm，口下方由活塞封闭一定质量的理想气体。已知活塞质量为4kg，横截面积为2cm2 ， 厚度可忽略，不计汽缸壁与活塞之间的摩擦。开始时活塞处于静止状态活塞与卡口之间的作用力为20N，现利用抽气机抽出汽缸内一部分气体，使活塞刚好与卡口间无作用力，抽出的气体充入到一导热性能良好的真空容器内，容器横截面积为1cm2 ， 高度为20cm。已知大气压强为p0=105Pa，环境温度保持不变，重力加速度g取10m/s2 ， 求此时充入气体的容器中气体压强。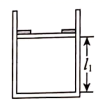
4. 一粗细均匀、两端封闭的U形玻璃管竖直放置，管内水银柱及空气柱长度如图所示，右侧水银柱长l1=20. 0cm，气体压强p1=70. 0cmHg，左侧水银柱长l2=35. 0cm，气体的长度l3=15. 0cm，现打开U形玻璃管右侧端口，求稳定后玻璃管左侧气体的长度将变为多少？设整个过程中气体温度保持不变，大气压强p0=75. 0cmHg（ ）
5. 如图所示，用细管连接A、B两个绝热的气缸，细管中有一可以自由移动的绝热活塞M，细管容积不计．A、B中分别装有完全相同的理想气体，初态的体积均为V1=1.0×10－2m3 ， 压强均为p1=1.0×105Pa，温度和环境温度相同且均为t1=27℃，A中导热活塞N的横截面积SA=500cm2 ． 现缓缓加热B中气体，保持A气体的温度不变，同时给N施加水平向右的推力，使活塞M的位置始终保持不变．稳定时，推力F= ×103N，外界大气压p0=1.0×105Pa，不计活塞与缸壁间的摩擦．求：
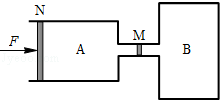
①活塞N向右移动的距离；
②B中气体的温度．(用摄氏度表示)
6. 如图所示，开口向上的汽缸C静置于水平桌面上，用一横截面积S=50cm2的轻质活塞封闭了一定质量的理想气体，一轻绳一端系在活塞上，另一端跨过两个定滑轮连着一劲度系数k=2800N/m的竖直轻弹簧A，A下端系有一质量m=14kg的物块B．开始时，缸内气体的温度t1=27℃，活塞到缸底的距离L1=120cm，弹簧恰好处于原长状态。已知外界大气压强恒为p0=1.0×105Pa，取重力加速度g=10m/s2 ， 不计一切摩擦。现使缸内气体缓慢冷却，求：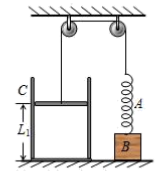
⑴当B刚要离开桌面时汽缸内封闭气体的温度；
⑵气体的温度冷却到-93℃时B离桌面的高度H．（结果保留两位有效数字）
7. 每年在元宵节的时候，我们都能看到很多市民在湘江边上放孔明灯祈福、许愿。如图，孔明灯的质量m＝0.2 kg、体积恒为 ，夜间空气温度 ，大气压强p0＝1.013×105 Pa，该条件下空气密度ρ0＝1.26 kg/m3。重力加速度 。点燃灯内蜡烛对灯内气体缓慢加热，直到灯刚能浮起时，求：
(i)灯内气体的密度ρ；
(ii)灯内气体温度为多少摄氏度.
8. 如图所示，汽缸开口向上固定在水平面上，其横截面积为S，内壁光滑，A，B为距离汽缸底部h2处的等高限位装置，限位装置上装有压力传感器，可探测活塞对限位装置的压力大小。活塞质量为m，在汽缸内封闭了一段高为hl、温度为T1的理想气体。对汽缸内气体缓缓降温，已知重力加速度为g，大气压强为p0 ， 变化过程中活塞始终保持水平状态。求：
①当活塞刚好与限位装置接触（无弹力）时，汽缸内气体的温度T2；
②当A，B处压力传感器的示数之和为2mg时，汽缸内气体的温度T3。
9. 如图所示，上端开口的光滑圆柱形汽缸竖直放置，横截面积为40cm2的活塞将一定质量的气体和一形状不规则的固体A封闭在汽缸内．在汽缸内距缸底60cm处设有a、b两限制装置，使活塞只能向上滑动．开始时活塞搁在a、b上，缸内气体的压强为P0(P0=1.0×105Pa为大气压强)，温度为300K，现缓慢加热汽缸内气体，当温度为360K时，活塞恰好离开a、b；当温度为396K时，活塞上升了3cm．g取10m/s2 ． 求：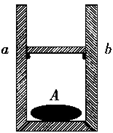
①当温度为360K时，缸内气体的压强；
②活塞的质量；
③固体A的体积．
10. 如图所示，水平固定放置的气缸，由截面积不同的两圆筒连接而成。活塞A、B面积分别为2S和S，汗塞A、B用长为2l的细直杆连接，活塞与筒壁气密性好且摩擦不计。现活塞间密闭有一定质量的理想气体，两活塞外侧(A的左方和B的右方)都是大气，大气压强始终保持为p0 ， 当气缸內气体温度为T0时，活塞B与两圆筒连接处的距离为l且处于静止状态。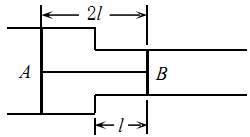
(i)现使气缸内气体温度缓慢下降，活塞A刚刚缓慢右移到两圆筒连接处时，求密闭气体的温度T1；
(ii)若气缸内气体温度缓慢下降至T0/2，求细直杆对活塞的弹力大小F
二、综合题
-
11. 如图所示，R为变阻箱，电压表为理想电压表，电源电动势 ，当变阻箱阻值为 时，闭合电键后，电压表读数 ，求：
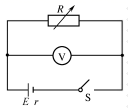(1)、电路中的电流I和电源内阻r；(2)、电源的输出功率P和效率 ；(3)、试推导说明当R为多大时，电源的输出功率最大。12. 热学中解决理想气体实验定律相关的问题时，经常使用 作为压强的单位，例如标准大气压 。如图所示。上端封闭、下端开口的细长的玻璃管固定在粗糙的斜面上。长为 的水银柱封闭了一段空气柱，空气柱的长度 。已知斜面的倾角 ，玻璃管与斜面的动摩擦因数 ，外界的压强为标准大气压，环境的温度保持不变， ， 。试求：
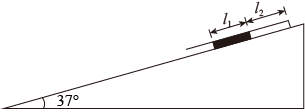(1)、此时玻璃管内气体的压强（用 作单位）。(2)、释放玻璃管，在玻璃管沿斜面下滑的过程中，管内空气柱的长度。13. 如图，绝热气缸a与导热气缸b、c均固定于地面，由刚性杆连接着的两个绝热活塞均可在气缸内无摩擦滑动。开始时a、b两个气缸内装有体积相等、温度均为T0的理想气体，真空气缸c的容积与此时a、b两个气缸中的气体体积相等，通过阀门与气缸b相连。现将阀门打开，稳定后，a中气体压强为原来的0.6倍，环境温度保持不变。
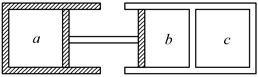(1)、求稳定后气缸a中气体的温度；(2)、请用热力学第一定律解释上述过程气缸a中气体温度变化的原因。14. 夏天游乐场经常见到如图甲所示的儿童玩具水枪，用手握住压力手柄，前后抽动，给储水瓶打气加压。打气加压完成后压力手柄位置不动，扣动扳机，水从枪口立即射出。其原理如图乙所示，储水瓶总容积为V0 ， 一开始灌入体积为0.8V0的水，瓶内空气压强与外界大气压强p0相等。已知打气筒每次把压强为p0、体积为0.02V0的空气压入瓶中，所有过程瓶中的气体温度保持不变，不考虑水的重力影响，求：
(1)、通过打气使储水瓶内气体压强为1.4p0时，扣动扳机让水连续射出待水不流出时（即储水瓶内气体压强与外界大气压强相等），储水瓶剩余水的体积；(2)、保持(1)问中剩余水量不变，若要使储水瓶内气体压强重新超过1.4p0 ， 至少需要打气的次数。15. 根据某种轮胎说明书可知，轮胎内气体压强的正常值在 至 之间，轮胎的容积 。已知当地气温 ，大气压强 ，设轮胎的容积和充气过程轮胎内气体的温度保持不变。(1)、若轮胎中原有气体的压强为 ，求最多可充入压强为 的气体的体积V；(2)、充好气的轮胎内气压 ，被运送到气温 的某地。为保证轮胎能正常使用，请通过计算说明是否需要充气。16. 如图所示，长为l＝100cm、上端开口、下端封闭、粗细均匀的玻璃管竖直放置，在玻璃管中注入长度为h＝25cm的水银柱，稳定后被封闭的空气柱的长度为l1＝51cm。现将玻璃管缓慢旋转 至开口向下竖直放置，此过程中被封闭的空气柱的温度保持不变，已知大气压强p0＝75cmHg。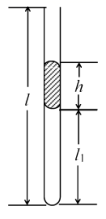
(1)、若玻璃管在旋转的过程中被封闭的空气柱的质量保持不变，求玻璃管开口向下时，管内空气柱的长度。(2)、若玻璃管在旋转的过程中被封闭的空气柱的质量发生了变化，当玻璃管开口向下时，管内水银柱的长度不变，且其下端恰好与管口相平，求空气柱质量的改变量Δm与原来封闭的空气柱的质量m的比值。17. 如图所示，一绝热汽缸固定在倾角为30°的固定斜面上，通过绝热活塞封闭着一定质量的理想气体，活塞的质量为 ，横截面积为S。初始时，气体的温度为 ，活塞与汽缸底部相距为L。通过电热丝缓慢加热气体，当气体吸收热量Q时，活塞上升到与汽缸底部相距2L处，已知大气压强为 ，重力加速度为g，不计活塞与汽缸壁之间的摩擦。求：
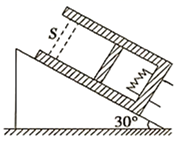(1)、此时气体的温度；(2)、加热过程中气体内能的增加量。18. 如图所示，一根粗细均匀、长 的细玻璃管 开口朝下竖直放置，玻璃管中有段长 的水银柱，上端封闭了一段长 的空气柱，外界大气温度为27℃，外界大气压强恒为 .现将玻璃管缓慢旋转至开口竖直向上，若空气柱可以看作理想气体，求：
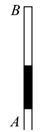(1)、开口竖直向上时，封闭空气柱的长度；(2)、再对B端缓慢加热，封闭气柱温度为多少开时，水银柱上端恰好上升到管口处.