河北省石家庄市2021届高三下学期数学质检试卷一

试卷更新日期：2021-04-23 类型：高考模拟

进入出卷网下载

一、单选题

1. 若集合 $A$ ， $B$ ， $U$ 满足： $A ⊊ B ⊊ U$ ，则 $U =$ （）

A、 $A \cup ∁_{U} B$ B、 $B \cup ∁_{U} A$ C、 $A \cap ∁_{U} B$ D、 $B \cap ∁_{U} A$

查看试题解析
2. 设向量 $\vec{a} = (1, 2)$ ， $\vec{b} = (m, - 1)$ ，且 $(\vec{a} + \vec{b}) ⊥ \vec{a}$ ，则实数 $m =$ （）

A、-3 B、 $\frac{3}{2}$ C、-2 D、 $- \frac{3}{2}$

查看试题解析
3. 甲、乙、丙三人从红、黄、蓝三种颜色的帽子中各选一顶戴在头上，每人帽子的颜色互不相同，乙比戴蓝帽的人个头高，丙和戴红帽的人身高不同，戴红帽的人比甲个头小，则甲、乙、丙所戴帽子的颜色分别为（）

A、红、黄、蓝 B、黄、红、蓝 C、蓝、红、黄 D、蓝、黄、红

查看试题解析
4. $a > 2$ 是 $a + \frac{2}{a} > 3$ 的（）

A、充要条件 B、必要不充分条件 C、充分不必要条件 D、既不充分也不必要条件

查看试题解析
5. 2021年是巩固脱贫攻坚成果的重要一年，某县为响应国家政策，选派了6名工作人员到 $A$ 、 $B$ 、 $C$ 三个村调研脱贫后的产业规划，每个村至少去1人，不同的安排方式共有（）

A、630种 B、600种 C、540种 D、480种

查看试题解析
6. 已知菱形 $A B C D$ 边长为2， $∠ A B C = 60 °$ ，沿对角线 $A C$ 折叠成三棱锥 $B^{'} - A C D$ ，使得二面角 $B^{'} - A C - D$ 为60°，设 $E$ 为 $B^{'} C$ 的中点， $F$ 为三棱锥 $B^{'} - A C D$ 表面上动点，且总满足 $A C ⊥ E F$ ，则点 $F$ 轨迹的长度为（）

A、 $2 \sqrt{3}$ B、 $3 \sqrt{3}$ C、 $\sqrt{3}$ D、 $\frac{3 \sqrt{3}}{2}$

查看试题解析
7. 已知数列 ${a_{n}}$ 的通项公式为 $a_{n} = n \sin \frac{n π}{3}$ ，则 $a_{1} + a_{2} + a_{3} + \dots + a_{2021} =$ （）

A、 $1011 \sqrt{3}$ B、 $- \frac{5}{2} \sqrt{3}$ C、 $\frac{5}{2} \sqrt{3}$ D、 $- 1011 \sqrt{3}$

查看试题解析
8. 若 $f (x)$ 图象上存在两点 $A$ ， $B$ 关于原点对称，则点对 $[A ， B]$ 称为函数 $f (x)$ 的“友情点对”（点对 $[A ， B]$ 与 $[B ， A]$ 视为同一个“友情点对”）若 $f (x) = {\begin{array}{l} \frac{x^{3}}{e^{x}} ， x \geq 0 \\ a x^{2} ， x < 0 \end{array}$ 恰有两个“友情点对”，则实数 $a$ 的取值范围是（）

A、 $(- \frac{1}{e} ， 0)$ B、 $(0 ， \frac{1}{e})$ C、 $(0 ， 1)$ D、 $(- 1 ， 0)$

查看试题解析

二、多选题

9. 关于 ${(1 - 2 x)}^{2021} = a_{0} + a_{1} \cdot x + a_{2} \cdot x^{2} + \dots + a_{2001} \cdot x^{2021} (x \in R)$ ，则（）

A、 $a_{0} = 1$ B、 $a_{1} + a_{2} + a_{3} + \dots + a_{2021} = 3^{2021}$ C、 $a_{3} = 8 C_{2021}^{3}$ D、 $a_{1} - a_{2} + a_{3} - a_{4} + \dots + a_{2021} = 1 - 3^{2021}$

查看试题解析
10. 设 $z$ 为复数，则下列命题中正确的是（）

A、 ${| z |}^{2} = z \bar{z}$ B、 $z^{2} = {| z |}^{2}$ C、若 $| z | = 1$ ，则 $| z + i |$ 的最大值为2 D、若 $| z - 1 | = 1$ ，则 $0 \leq | z | \leq 2$

查看试题解析
11. 函数 $f (x) = 2 \sin (ω x + φ) (ω > 0 ， 0 < φ < π)$ 的图象如图，把函数 $f (x)$ 的图象上所有的点向右平移 $\frac{π}{6}$ 个单位长度，可得到函数 $y = g (x)$ 的图象，下列结论正确的是（）

A、 $φ = \frac{π}{3}$ B、函数 $g (x)$ 的最小正周期为 $π$ C、函数 $g (x)$ 在区间 $[- \frac{π}{3} ， \frac{π}{12}]$ 上单调递增 D、函数 $g (x)$ 关于点 $(- \frac{π}{3} ， 0)$ 中心对称

查看试题解析
12. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左右焦点分别为 $F_{1}$ 、 $F_{2}$ ，长轴长为4，点 $P (\sqrt{2} ， 1)$ 在椭圆内部，点 $Q$ 在椭圆上，则以下说法正确的是（）

A、离心率的取值范围为 $(0 ， \frac{1}{2})$ B、当离心率为 $\frac{\sqrt{2}}{4}$ 时， $| Q F_{1} | + | Q P |$ 的最大值为 $2 a + \frac{\sqrt{6}}{2}$ C、存在点 $Q$ 使得 $\vec{Q F_{1}} \cdot \vec{Q F_{2}} = 0$ D、 $\frac{1}{| Q F_{1} |} + \frac{1}{| Q F_{2} |}$ 的最小值为1

查看试题解析

三、填空题

13. 已知随机变量 $X$ 服从正态分布 $N (10, σ^{2})$ ，若 $P (X < 8) = 0.23$ ，则 $P (X < 12) =$ .

查看试题解析
14. 如图所示，一个圆锥的侧面展开图为以 $A$ 为圆心，半径长为2的半圆，点 $D$ 、 $M$ 在 $\overset{⌢}{B C}$ 上，且 $\overset{⌢}{B D}$ 的长度为 $\frac{π}{3}$ ， $\overset{⌢}{B M}$ 的长度为 $π$ ，则在该圆锥中，点 $M$ 到平面 $A B D$ 的距离为.

查看试题解析
15. 已知定义在 $R$ 上的函数 $f (x)$ ，其导函数为 $f^{'} (x)$ ，满足 $f^{'} (x) > 2$ ， $f (2) = 4$ ，则不等式 $x f (x - 1) > 2 x^{2} - 2 x$ 的解集为.

查看试题解析
16. 已知抛物线 $y^{2} = 2 p x (p > 0)$ 的焦点为 $F$ ，过 $F$ 且被抛物线截得的弦长为2的直线有且仅有两条，写出一个满足条件的抛物线的方程，此时该弦中点到 $y$ 轴的距离为.

查看试题解析

四、解答题

17. 已知公差不为0的等差数列 ${a_{n}}$ 满足 $a_{1} = 1$ ，且 $a_{1}$ ， $a_{2}$ ， $a_{5}$ 成等比数列.
（Ⅰ）求数列 ${a_{n}}$ 的通项公式；

（Ⅱ）若 $b_{n} = 2^{n - 1}$ ，求数列 ${a_{n} \cdot b_{n}}$ 的前 $n$ 项和 $T_{n}$ .

查看试题解析
18. 在 $△ A B C$ 中，角 $A$ ， $B$ ， $C$ 所对的边分别为 $a$ ， $b$ ， $c$ ，满足 $\sqrt{3} c = b (\sin A + \sqrt{3} \cos A)$ .
（Ⅰ）求角 $B$ 的大小；

（Ⅱ）若 $a + c = 2$ ，求 $b$ 的取值范围.

查看试题解析
19. 2022年北京冬奥会标志性场馆——国家速滑馆的设计理念来源于一个冰和速度结合的创意，沿着外墙面由低到高盘旋而成的“冰丝带”，就像速度滑冰运动员高速滑动时留下的一圈圈风驰电掣的轨迹，冰上划痕成丝带，22条“冰丝带”又象征北京2022年冬奥会.其中“冰丝带”呈现出圆形平面、椭圆形平面、马鞍形双曲面三种造型，这种造型富有动感，体现了冰上运动的速度和激情这三种造型取自于球、椭球、椭圆柱等空间几何体，其设计参数包括曲率、挠率、面积体积等对几何图形的面积、体积计算方法的研究在中国数学史上有过辉煌的成就，如《九章算术》中记录了数学家刘徽提出利用牟合方盖的体积来推导球的体积公式，但由于不能计算牟合方盖的体积并没有得出球的体积计算公式直到200年以后数学家祖冲之、祖眶父子在《缀术》提出祖暅原理：“幂势既同，则积不容异”，才利用牟合方盖的体积推导出球的体积公式原理的意思是：两个等高的几何体若在所有等高处的水平截面的面积相等，则这两个几何体的体积相等.

（Ⅰ）利用祖暅原理推导半径为 $R$ 的球的体积公式时，可以构造如图②所示的几何体 $M$ ，几何体 $M$ 的底面半径和高都为 $R$ ，其底面和半球体的底面同在平面 $α$ 内.设与平面 $α$ 平行且距离为 $d$ 的平面 $β$ 截两个几何体得到两个截面，请在图②中用阴影画出与图①中阴影截面面积相等的图形并给出证明；

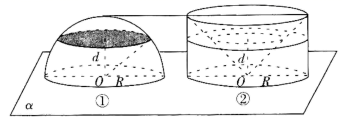
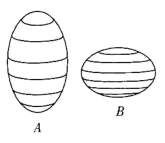
（Ⅱ）现将椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 所围成的椭圆面分别绕其长轴、短轴旋转一周后得两个不同的椭球 $A$ ， $B$ （如图），类比（Ⅰ）中的方法，探究椭球 $A$ 的体积公式，并写出椭球 $A$ ， $B$ 的体积之比.

查看试题解析
20. “T2钻石联赛”是世界乒联推出一种新型乒乓球赛事，其赛制如下：采用七局四胜制，比赛过程中可能出现两种模式：“常规模式”和“FAST5模式”.在前24分钟内进行的常规模式中，每小局比赛均为11分制，率先拿满1分的选手赢得该局；如果两名球员在24分钟内都没有人赢得4局比赛，那么将进入“FAST5”模式，“FAST5”模式为5分制的小局比赛，率先拿满5分的选手赢得该局.24分钟计时后开始的所有小局均采用“FAST5”模式.某位选手率先在7局比赛中拿下4局，比赛结束.现有甲、乙两位选手进行比赛，经统计分析甲、乙之间以往比赛数据发现，24分钟内甲、乙可以完整打满2局或3局，且在11分制比赛中，每局甲获胜的概率为 $\frac{2}{3}$ ，乙获胜的概率为 $\frac{1}{3}$ ；在“FAST5”模式，每局比赛双方获胜的概率都为 $\frac{1}{2}$ ，每局比赛结果相互独立.
（Ⅰ）求4局比赛决出胜负的概率；

（Ⅱ）设在24分钟内，甲、乙比赛了3局，比赛结束时，甲乙总共进行的局数记为 $X$ ，求 $X$ 的分布列及数学期望.

查看试题解析
21. 已知坐标原点为 $O$ ，双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的焦点到其渐近线的距离为 $\sqrt{2}$ ，离心率为 $\sqrt{3}$ .
（Ⅰ）求双曲线的方程；

（Ⅱ）设过双曲线上动点 $P (x_{0} ， y_{0})$ 的直线 $x_{0} x - \frac{y_{0} y}{2} = 1$ 分别交双曲线的两条渐近线于 $A$ ， $B$ 两点，求 $△ A O B$ 的外心 $M$ 的轨迹方程.

查看试题解析
22. 已知函数 $f (x) = \frac{- x \sin x}{\cos x}$ ，且方程 $f (x) - a = 0$ 在 $[\frac{2 π}{3} ， \frac{3 π}{4}]$ 上有解.
（Ⅰ）求实数 $a$ 的取值范围；

（Ⅱ）设函数 $g (x) = (a + 1) \sin x - x \cos x (x \in [\frac{π}{2} ， π])$ 的最大值为 $G (a)$ ，求函数 $G (a)$ 的最小值；

查看试题解析