河北省邯郸市2021届高三数学一模试卷
试卷更新日期:2021-04-23 类型:高考模拟
一、单选题
-
1. 已知集合 , ( )A、 B、 C、 D、2. 已知复数 ,则 ( )A、2 B、-2 C、4 D、63. 已知 ,则 ( )A、 B、 C、 D、4. 函数 的部分图象大致是( )A、
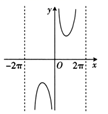 B、
B、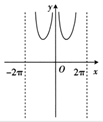 C、
C、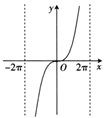 D、
D、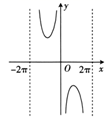 5. 构建德智体美劳全面培养的教育体系是我国教育一直以来努力的方向.某中学积极响应党的号召,开展各项有益于德智体美劳全面发展的活动.如图所示的是该校高三(1)、(2)班两个班级在某次活动中的德智体美劳的评价得分对照图(得分越高,说明该项教育越好).下列说法正确的是( )
5. 构建德智体美劳全面培养的教育体系是我国教育一直以来努力的方向.某中学积极响应党的号召,开展各项有益于德智体美劳全面发展的活动.如图所示的是该校高三(1)、(2)班两个班级在某次活动中的德智体美劳的评价得分对照图(得分越高,说明该项教育越好).下列说法正确的是( )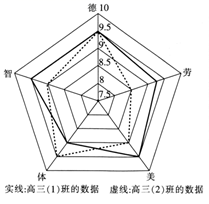 A、高三(2)班五项评价得分的极差为1.5 B、除体育外,高三(1)班的各项评价得分均高于高三(2)班对应的得分 C、高三(1)班五项评价得分的平均数比高三(2)班五项评价得分的平均数要高 D、各项评价得分中,这两班的体育得分相差最大6. 已知抛物线 的焦点为F , P为C在第一象限上一点,若 的中点到y轴的距离为3,则直线 的斜率为( )A、 B、 C、2 D、47. 设 是双曲线 的两个焦点,O为坐标原点,点 在C的左支上,且 ,则 的面积为( )A、8 B、 C、4 D、8. 中国古典乐器一般按“八音”分类,这是我国最早按乐器的制造材料来对乐器进行分类的方法,最早见于《周礼·春官·大师》.八音分为“金、石、土、革、丝、木、鲍、竹”,其中“金、石、木、革”为打击乐器,“土、鲍、竹”为吹奏乐器,“丝”为弹拨乐器.某同学安排了包括“土、鲍、竹”在内的六种乐器的学习,每种乐器安排一节,连排六节,并要求“土”与“鲍”相邻排课,但均不与“竹”相邻排课,且“丝”不能排在第一节,则不同的排课方式的种数为( )A、960 B、1024 C、1296 D、20219. 函数 的图象向右平移 个单位长度后得到函数 的图象,对于函数 ,下列说法不正确的是( )A、 的最小正周期为 B、 的图象关于直线 对称 C、 在区间 上单调递增 D、 的图象关于点 对称
A、高三(2)班五项评价得分的极差为1.5 B、除体育外,高三(1)班的各项评价得分均高于高三(2)班对应的得分 C、高三(1)班五项评价得分的平均数比高三(2)班五项评价得分的平均数要高 D、各项评价得分中,这两班的体育得分相差最大6. 已知抛物线 的焦点为F , P为C在第一象限上一点,若 的中点到y轴的距离为3,则直线 的斜率为( )A、 B、 C、2 D、47. 设 是双曲线 的两个焦点,O为坐标原点,点 在C的左支上,且 ,则 的面积为( )A、8 B、 C、4 D、8. 中国古典乐器一般按“八音”分类,这是我国最早按乐器的制造材料来对乐器进行分类的方法,最早见于《周礼·春官·大师》.八音分为“金、石、土、革、丝、木、鲍、竹”,其中“金、石、木、革”为打击乐器,“土、鲍、竹”为吹奏乐器,“丝”为弹拨乐器.某同学安排了包括“土、鲍、竹”在内的六种乐器的学习,每种乐器安排一节,连排六节,并要求“土”与“鲍”相邻排课,但均不与“竹”相邻排课,且“丝”不能排在第一节,则不同的排课方式的种数为( )A、960 B、1024 C、1296 D、20219. 函数 的图象向右平移 个单位长度后得到函数 的图象,对于函数 ,下列说法不正确的是( )A、 的最小正周期为 B、 的图象关于直线 对称 C、 在区间 上单调递增 D、 的图象关于点 对称二、多选题
-
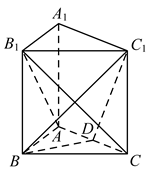
10. 攒尖是我国古代建筑中屋顶的一种结构形式,宋代称为最尖,清代称攒尖,通常有圆形攒尖、三角攒尖、四角攒尖、八角攒尖,也有单檐和重檐之分,多见于亭阁式建筑,园林建筑.下面以四角攒尖为例,如图,它的屋顶部分的轮廓可近似看作一个正四棱锥.已知此正四棱锥的侧面与底面所成的锐二面角为 ,这个角接近 ,若取 ,侧棱长为 米,则( )
 A、正四棱锥的底面边长为6米 B、正四棱锥的底面边长为3米 C、正四棱锥的侧面积为 平方米 D、正四棱锥的侧面积为 平方米11. 新学期到来,某大学开出了新课“烹饪选修课”,面向2020级本科生开放.该校学生小华选完内容后,其他三位同学根据小华的兴趣爱好对他选择的内容进行猜测.甲说:小华选的不是川菜干烧大虾,选的是烹制中式面食.乙说:小华选的不是烹制中式面食,选的是烹制西式点心.丙说:小华选的不是烹制中式面食,也不是家常菜青椒土豆丝.已知三人中有一个人说的全对,有一个人说的对了一半,剩下的一个人说的全不对,由此推断小华选择的内容( )A、可能是家常菜青椒土豆丝 B、可能是川菜干烧大虾 C、可能是烹制西式点心 D、可能是烹制中式面食12. 已知函数 ,若关于x的方程 恰有两个不同解 ,则 的取值可能是( )A、-3 B、-1 C、0 D、2
A、正四棱锥的底面边长为6米 B、正四棱锥的底面边长为3米 C、正四棱锥的侧面积为 平方米 D、正四棱锥的侧面积为 平方米11. 新学期到来,某大学开出了新课“烹饪选修课”,面向2020级本科生开放.该校学生小华选完内容后,其他三位同学根据小华的兴趣爱好对他选择的内容进行猜测.甲说:小华选的不是川菜干烧大虾,选的是烹制中式面食.乙说:小华选的不是烹制中式面食,选的是烹制西式点心.丙说:小华选的不是烹制中式面食,也不是家常菜青椒土豆丝.已知三人中有一个人说的全对,有一个人说的对了一半,剩下的一个人说的全不对,由此推断小华选择的内容( )A、可能是家常菜青椒土豆丝 B、可能是川菜干烧大虾 C、可能是烹制西式点心 D、可能是烹制中式面食12. 已知函数 ,若关于x的方程 恰有两个不同解 ,则 的取值可能是( )A、-3 B、-1 C、0 D、2三、填空题
-
13. 已知平面向量 ,非零向量 满足 ,则 . (答案不唯一,写出满足条件的一个向量坐标即可)14. 已知 ,则 的最小值为 .15. 已知函数 满足 ,则曲线 在点 处的切线斜率为 .16. 在正四棱锥 中, ,若四棱锥 的体积为 ,则该四棱锥外接球的体积为 .
四、解答题
-
17. 已知各项均为正数的等差数列 的公差为4,其前n项和为 且 为 的等比中项(1)、求 的通项公式;18. 设 的内角A , B , C的对边分别为a , b , c , 且满足(1)、求 的值;(2)、若点D为边 的中点, ,求 的值.19. 为了树立和践行绿水青山就是金山银山的理念,加强环境的治理和生态的修复,某市在其辖区内某一个县的27个行政村中各随机选择农田土壤样本一份,对样本中的铅、锦、铭等重金属的含量进行了检测,并按照国家土壤重金属污染评价级标准(清洁、尚清洁、轻度污染、中度污染、重度污染)进行分级,绘制了如图所示的条形图
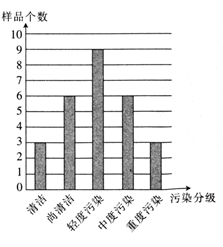 (1)、从轻度污染以上(包括轻度污染)的行政村中按分层抽样的方法抽取6个,求在轻度、中度、重度污染的行政村中分别抽取的个数;(2)、规定:轻度污染记污染度为1,中度污染记污染度为2,重度污染记污染度为3.从(1)中抽取的6个行政村中任选3个,污染度的得分之和记为X , 求X的数学期望.
(1)、从轻度污染以上(包括轻度污染)的行政村中按分层抽样的方法抽取6个,求在轻度、中度、重度污染的行政村中分别抽取的个数;(2)、规定:轻度污染记污染度为1,中度污染记污染度为2,重度污染记污染度为3.从(1)中抽取的6个行政村中任选3个,污染度的得分之和记为X , 求X的数学期望.