吉林省名校调研系列卷2020-2021学年七年级下学期数学第一次月考试卷
试卷更新日期:2021-04-23 类型:月考试卷
一、选择题(每小题2分,共12分)
-
1. 如图,不是平移设计的是( )A、
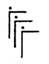 B、
B、 C、
C、 D、
D、 2. 在下面四个图形中, 与 是对顶角的是( ).A、
2. 在下面四个图形中, 与 是对顶角的是( ).A、 B、
B、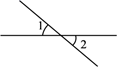 C、
C、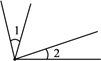 D、
D、 3. 如图,下列说法错误的是( )
3. 如图,下列说法错误的是( ) A、∠A与∠B是同旁内角 B、∠1与∠3是同位角 C、∠2与∠A是同位角 D、∠2与∠3是内错角4. 如图,AC⊥BC,AC=4,点D是线段BC上的动点,则A,D两点之间的距离不可能是( )
A、∠A与∠B是同旁内角 B、∠1与∠3是同位角 C、∠2与∠A是同位角 D、∠2与∠3是内错角4. 如图,AC⊥BC,AC=4,点D是线段BC上的动点,则A,D两点之间的距离不可能是( )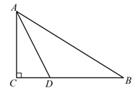 A、3.5 B、4.5 C、5 D、5.55. 如图,因为AB⊥l,BC⊥l,B为垂足,所以AB和BC重合,其理由是( )
A、3.5 B、4.5 C、5 D、5.55. 如图,因为AB⊥l,BC⊥l,B为垂足,所以AB和BC重合,其理由是( )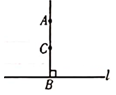 A、两点确定一条直线 B、在同一平面内,过一点有且只有一条直线与已知直线垂直 C、垂直同一条直线的两条直线平行 D、垂线段最短6. 如图,直线AB∥CD∥EF,点O在直线EF上,下列结论正确的是( )
A、两点确定一条直线 B、在同一平面内,过一点有且只有一条直线与已知直线垂直 C、垂直同一条直线的两条直线平行 D、垂线段最短6. 如图,直线AB∥CD∥EF,点O在直线EF上,下列结论正确的是( )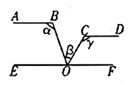 A、∠a+∠β-∠γ= 90° B、∠a+∠r-∠β=180° C、∠y+∠β-∠a=180° D、∠a+∠β+∠γ=180°
A、∠a+∠β-∠γ= 90° B、∠a+∠r-∠β=180° C、∠y+∠β-∠a=180° D、∠a+∠β+∠γ=180°二、填空题(每小题3分,共24分)
-
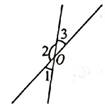
7. 将“两直线平行,同位角相等”改写成“如果……那么……的形式是 。8. 如图,两直线交于点O,若∠1=34°,则∠2=°;∠3 =°。
 9. 如图,若∠1=∠2=∠3=54°,则∠4= °。
9. 如图,若∠1=∠2=∠3=54°,则∠4= °。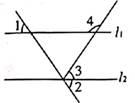 10. 如图,一把长方形直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若∠CBD=55°,
10. 如图,一把长方形直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若∠CBD=55°,则∠EDA的度数是。
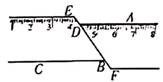 11. 如图,AB⊥l1 , AC⊥l2 , 若AB=4,BC=3,AC=5,则点A到直线l1的距离是。
11. 如图,AB⊥l1 , AC⊥l2 , 若AB=4,BC=3,AC=5,则点A到直线l1的距离是。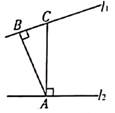 12. 如图,要使BE∥DF,需补充一个条件,你认为这个条件应该是(填一个条件即可)。
12. 如图,要使BE∥DF,需补充一个条件,你认为这个条件应该是(填一个条件即可)。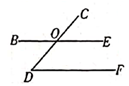 13. 如图是一块电脑主板的示意图,每一转角处都是直角,数据如图所示(单位:mm),则该主板的周长是 mm。
13. 如图是一块电脑主板的示意图,每一转角处都是直角,数据如图所示(单位:mm),则该主板的周长是 mm。 14. 将一副常规直角三角板和一张对边平行的纸条按如图方式摆放,两个三角板的一直角边重合其中一个三角板的斜边与纸条一边重合,则∠1的度数是 。
14. 将一副常规直角三角板和一张对边平行的纸条按如图方式摆放,两个三角板的一直角边重合其中一个三角板的斜边与纸条一边重合,则∠1的度数是 。
三、解答题(每小题5分,共20分)
-
15. 如图,∠1+∠2=180°。求证:a∥b。
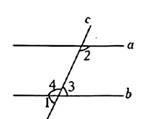 16. 如图,直线AB、CD相交于点O,OE把∠BOD分成两部分,若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数。
16. 如图,直线AB、CD相交于点O,OE把∠BOD分成两部分,若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数。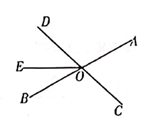 17. 如图,在每个小正方形的边长均为1的方格纸中,三角形ABC的顶点都在方格纸的格点上,将三角形ABC先向左平移2格,再向上平移4格。
17. 如图,在每个小正方形的边长均为1的方格纸中,三角形ABC的顶点都在方格纸的格点上,将三角形ABC先向左平移2格,再向上平移4格。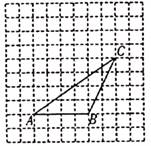 (1)、请在图中画出平移后的三角形A'B'C';(2)、求出三角形ABC的面积。18. 如图,已知直线AB和CD相父于点O,OM平分∠BOD,∠MON=90°,∠AOC=50°,
(1)、请在图中画出平移后的三角形A'B'C';(2)、求出三角形ABC的面积。18. 如图,已知直线AB和CD相父于点O,OM平分∠BOD,∠MON=90°,∠AOC=50°,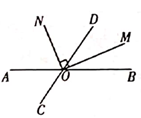 (1)、求∠AON的度数;(2)、写出∠DON的余角。
(1)、求∠AON的度数;(2)、写出∠DON的余角。四、解答题(每小题7分,共28分)
-
19. 如图,∠1=∠2,∠3=∠E.求:AD∥BE。
 20. 如图,AB、CD相交于点E,∠ACE=∠AEC,∠BDE=∠BED,过点A作AF⊥BD,垂足为F。求证:AC⊥AF(请把下面的证明过程补充完整)。
20. 如图,AB、CD相交于点E,∠ACE=∠AEC,∠BDE=∠BED,过点A作AF⊥BD,垂足为F。求证:AC⊥AF(请把下面的证明过程补充完整)。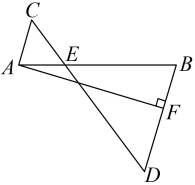
证明:∵∠ACE=∠AEC,∠BDE=∠BED,
又∠AEC=∠BED,()
∴∠ACE=∠BDE.
∴AC∥DB,()
∴∠CAF=∠AFD,()
∵AF⊥DB,
∵∠AFD=90°,()
∴∠CAF=90°,
∴AC⊥AF。
21. 如图,某工程队从A点出发,沿北偏西67°方向修一条公路AD,在BD路段出现中塌陷区,就改变方向,由B点沿北偏东23°方向继续修建B段,到达C点又改变方向,使所修路段CE∥AB,求此时∠ECB的度数,并说明理由。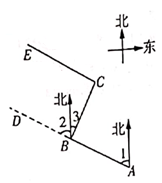 22. 如图,EF∥AB,∠DCB=65°,∠CBF=20°,∠EFB=135°。
22. 如图,EF∥AB,∠DCB=65°,∠CBF=20°,∠EFB=135°。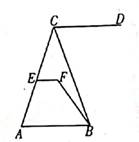 (1)、向直线CD与AB有怎样的位置关系?并说明理由;(2)、若∠CEF=60°,求∠ACB的度数。
(1)、向直线CD与AB有怎样的位置关系?并说明理由;(2)、若∠CEF=60°,求∠ACB的度数。五、解答题(每小题8分,共16分)
-
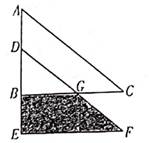
23. 如图,已知三角形ABC中,∠ABC=90°,边BC=12cm,把三角形ABC向下平移至三角形DEF后,AD=5cm,GC=4cm,请求出图中阴影部分的面积。
 24. 如图,在三角形ABC的三边上有D、E、F三点,点G在线段DF上,∠1与∠2互补,∠3=∠C。
24. 如图,在三角形ABC的三边上有D、E、F三点,点G在线段DF上,∠1与∠2互补,∠3=∠C。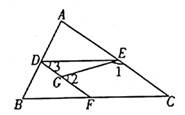 (1)、若∠C=40°,求∠BFD的度数;(2)、判断DE与BC的位置关系,并说明理由。
(1)、若∠C=40°,求∠BFD的度数;(2)、判断DE与BC的位置关系,并说明理由。六、解答题(每小题10分,共20分)
-
25. 一副常规直角三角板中的两块直角三角板的直角顶点(按如图方式叠放在一起,已知∠A=60°,∠D=30°,∠E=∠B=45°。
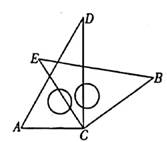 (1)、若∠DCE=50°.则∠ACB的度数为;(2)、由(1)猜想∠ACB与∠DCE的数量关系,并说明理由;(3)、若∠ACE<90°且点E在直线AC的上方,当这两块直角三角板有一组边互相平行时,请直接写出∠ACE角度所有可能的值。26. 如图.直线l1∥l2 , 直线EF和直线l1、l2分别交于C、D两点,点A、B分别在直线l1、l2上,点P在直线EF上,连接:PA、PB。
(1)、若∠DCE=50°.则∠ACB的度数为;(2)、由(1)猜想∠ACB与∠DCE的数量关系,并说明理由;(3)、若∠ACE<90°且点E在直线AC的上方,当这两块直角三角板有一组边互相平行时,请直接写出∠ACE角度所有可能的值。26. 如图.直线l1∥l2 , 直线EF和直线l1、l2分别交于C、D两点,点A、B分别在直线l1、l2上,点P在直线EF上,连接:PA、PB。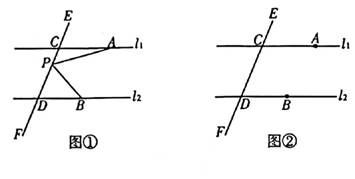 (1)、猜想:如图①,若点P在线段CD上,∠PAC=15°,∠PBD=40°,则∠APB的大小为度;(2)、探究:如图①,若点P在线段CD上,直接写出∠PAC、∠APB、∠PBD之间的数量关系;(3)、拓展:如图②,若点P在射线CE上或在射线DF上时,请探究∠PAC、∠APB、∠PBD之间的数量关系。
(1)、猜想:如图①,若点P在线段CD上,∠PAC=15°,∠PBD=40°,则∠APB的大小为度;(2)、探究:如图①,若点P在线段CD上,直接写出∠PAC、∠APB、∠PBD之间的数量关系;(3)、拓展:如图②,若点P在射线CE上或在射线DF上时,请探究∠PAC、∠APB、∠PBD之间的数量关系。