山西省临汾市侯马市2019-2020学年八年级下学期数学期末试卷

试卷更新日期：2021-04-23 类型：期末考试

进入出卷网下载

一、单选题

1. 若分式 $\frac{x - 3}{x + 4}$ 的值为0，则x的值是（）

A、 $x = 3$ B、 $x = 0$ C、 $x = - 3$ D、 $x = - 4$

查看试题解析
2. 已知点A（3m+1，﹣2）在第三象限，则m的取值范围是（）

A、m＜﹣ $\frac{1}{3}$ B、m＞﹣ $\frac{1}{3}$ C、m≤﹣ $\frac{1}{3}$ D、m≥﹣ $\frac{1}{3}$

查看试题解析
3. 如图，平行四边形ABCD的对角线交于点O，且AB＝5，△OCD的周长为21，则对角线AC与BD的和是（）

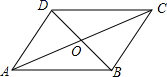A、16 B、21 C、32 D、42

查看试题解析
4. 甲、乙、丙、丁四人进行射击测试，射击成绩的平均数都约为8.8环，方差分别为S_甲²＝0.63，S_乙²＝0.42，S_丙²＝0.48，S_丁²＝0.51，则四人中成绩最稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
5. 新型冠状病毒“COVID﹣19”的平均半径约为50纳米（1纳米＝10^﹣9米），这一数据用科学记数法表示，正确的是（）

A、50×10^﹣9米 B、5.0×10^﹣9米 C、5.0×10^﹣8米 D、0.5×10^﹣7米

查看试题解析
6. 下列能够判定一个四边形是正方形的条件是（）
①一组邻边相等且对角线相等并互相平分；

②对角线互相垂直平分；

③四条边相等且四个内角也相等；

④对角线相等的菱形．

A、①②④ B、①③④ C、③④ D、①②③④

查看试题解析
7. 已知点A（1，y₁）、B（2，y₂）、C（﹣3，y₃）都在反比例函数 $y = \frac{6}{x}$ 的图象上，则y₁、y₂、y₃的大小关系是( )

A、y₃＜y₁＜y₂ B、y₁＜y₂＜y₃ C、y₂＜y₁＜y₃ D、y₃＜y₂＜y₁

查看试题解析
8. 如图，小聪在作线段AB的垂直平分线时，他是这样操作的：分别以A和B为圆心，大于 $\frac{1}{2}$ AB的长为半径画弧，两弧相交于C，D，则直线CD即为所求．根据他的作图方法可知四边形ADBC一定是（）

A、矩形 B、菱形 C、正方形 D、等腰梯形

查看试题解析
9. 如图，矩形ABCD的对角线AC与BD交于点O ，过点O作BD的垂线分别交AD ， BC于E ， F两点．若AC＝2 $\sqrt{3}$ ，∠DAO＝30°，则FC的长度为(　　)

A、1 B、2 C、 $\sqrt{2}$ D、 $\sqrt{3}$

查看试题解析
10. 如图，点 P 是反比例函数 y =6/x的图象上的任意一点，过点 P分别作两坐标轴的垂线，与坐标轴构成矩形 OAPB，点 D 是矩形OAPB 内任意一点，连接 DA、DB、DP、DO，则图中阴影部分的面积（）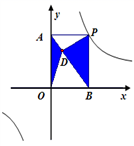

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 一组数据5，－2，3，x，3，－2，若每个数据都是这组数据的众数，则这组数
据的平均数是．

查看试题解析
12. 如图，把矩形ABCD纸片沿着过点A的直线AE折叠，使得点D落在BC边上的点F处，若∠BAF＝40°，则∠DAE＝°．

查看试题解析
13. 若关于若关于x的分式方程 $\frac{2 x - a}{x - 1} = 1$ 的解为正数，那么字母a的取值范围是.

查看试题解析
14. 如图，已知矩形ABCD，AB在y轴上，AB=2，BC=3，点A的坐标为(0，1)，在AD边上有一点E(2，1)，过点E的直线与BC交于点F．若EF平分矩形ABCD的面积，则直线EF的解析式为。

查看试题解析
15. 在一条笔直的公路上有A、B、C三地，C地位于A、B两地之间，甲车从A地沿这条公路匀速驶向C地，乙车从B地沿这条公路匀速驶向A地，在甲车出发至甲车到达C地的过程中，甲、乙两车各自与C地的距离y（km）与甲车行驶时间t（h）之间的函数关系如图所示．下列结论：①甲车出发2h时，两车相遇；②乙车出发1.5h时，两车相距170km；③乙车出发2 $\frac{5}{7}$ h时，两车相遇；④甲车到达C地时，两车相距40km．其中正确的是（填写所有正确结论的序号）．

查看试题解析

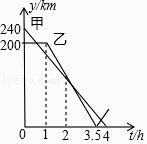
三、解答题

16.

(1)、计算： $\sqrt{4} + {(π - 2)}^{0} - | - 5 | + {(\frac{2}{3})}^{- 2}$ ；

(2)、化简： $\frac{2 x}{x + 1} - \frac{2 x + 4}{x^{2} - 1} \div \frac{x + 2}{x^{2} - 2 x + 1}$ ．

查看试题解析

17. 为让同学们更深入的了解新冠病毒，某校举办了一场新冠病毒知识竞赛，满分10分，学生得分为整数，成绩达到6分以上（包括6分）为合格，达到9分以上（包含9分）为优秀．这次竞赛中甲乙两组学生成绩分布的条形统计图如图所示．

(1)、补充完成下面的成绩统计分析表；

组别	平均数	中位数	方差	合格率	优秀率
甲组	6.7		3.41	90%	20%
乙组		7.5		70%	10%

(2)、小明同学说：“这次竞赛我得了7分，在我们小组中排名属中游略偏上!”观察上表可知，小明是组的学生；（填“甲”或“乙”）

(3)、甲组同学说他们组的成绩好于乙组，因为他们组的合格率、优秀率均高于乙组，但乙组同学不同意，认为他们组的成绩要好于甲组．请你给出两条支持乙组同学观点的理由．

查看试题解析

18. 已知函数y₁＝﹣x和y₂＝﹣ $\frac{4}{x}$ ．

(1)、在同一个平面直角坐标系中画出这两个函数的图象；

(2)、根据图象，写出它们的交点坐标；

(3)、根据图象，说明当x取什么值时，y₁＞y₂？

查看试题解析
19. 在校园手工制作活动中，现有甲、乙两人接到手工制作纸花任务，已知甲每小时制作纸花比乙每小时制作纸花少20朵，甲制作240朵纸花的时间与乙制作320朵纸花的时间相同，求乙每小时制作多少朵纸花？

查看试题解析
20. 如图，点E是正方形ABCD的边CD上的一点，点F是CB的延长线上一点，且DE＝BF，问线段AE与线段AF之间有何关系，并说明理由．

查看试题解析
21. 如图，在菱形ABCD中，∠ABC＝120°，点E是边AB的中点，P是对角线AC上的一个动点，若AB＝2 $\sqrt{3}$ ，求PB+PE的最小值是多少？

查看试题解析
22. 已知，在直角坐标系中，平行四边形OABC的顶点A，C坐标分别为A(2，0)，C(－1，2)，反比例函数 $y = \frac{m}{x}$ 的图象经过点B (m≠0)

(1)、求出反比例函数的解析式

(2)、将 $▱$ OABC沿着x轴翻折，点C落在点D处，做出点D并判断点D是否在反比例函数 $y = \frac{m}{x}$ 的图象上

(3)、在x轴是否存在一点P使△OCP为等腰三角形，若存在，写出点P的坐标；若不存在，请说明理由．

查看试题解析
23. 如图，正方形ABCO的边OA、OC在坐标轴上，点B坐标为（6，6），将正方形ABCO绕点C逆时针旋转角度α（0°＜α＜90°），得到正方形CDEF ， ED交线段AB于点G ， ED的延长线交线段OA于点H ，连结CH、CG ．

(1)、求证：CG平分∠DCB；

(2)、在正方形ABCO绕点C逆时针旋转的过程中，求线段HG、OH、BG之间的数量关系；

(3)、连结BD、DA、AE、EB ，在旋转的过程中，四边形AEBD是否能在点G满足一定的条件下成为矩形？若能，试求出直线DE的解析式；若不能，请说明理由．

查看试题解析