山西省晋中市寿阳县2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2021-04-23 类型:期末考试
一、单选题
-
1. 在以下”绿色食品、响应环保、可回收物、节水“四个标志图案中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知a<b , 则下列不等式正确的是( )A、a﹣3<b﹣3 B、 > C、﹣a<﹣b D、6a>6b3. 下列各式从左到右的变形,属于因式分解的是( )A、 B、 C、 D、4. 若分式 有意义,则x的取值应该该满足( )A、x= B、x= C、x≠ D、x≠5. 甲、乙二人做某种机械零件,已知每小时甲比乙少做8个,甲做120个所用的时间与乙做150个所用的时间相等,设甲每小时做x个零件,下列方程正确的是( )A、 B、 C、 D、6. 如图.已知四边形ABCD是平行四边形,结合作图痕迹,下列说法错误的是( )
2. 已知a<b , 则下列不等式正确的是( )A、a﹣3<b﹣3 B、 > C、﹣a<﹣b D、6a>6b3. 下列各式从左到右的变形,属于因式分解的是( )A、 B、 C、 D、4. 若分式 有意义,则x的取值应该该满足( )A、x= B、x= C、x≠ D、x≠5. 甲、乙二人做某种机械零件,已知每小时甲比乙少做8个,甲做120个所用的时间与乙做150个所用的时间相等,设甲每小时做x个零件,下列方程正确的是( )A、 B、 C、 D、6. 如图.已知四边形ABCD是平行四边形,结合作图痕迹,下列说法错误的是( )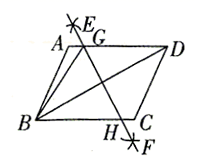 A、 与 垂直 B、 C、 平分 D、若 的周长为4,则平行四边形 的周长为87. 如图,四边形ABCD是边长为5cm的菱形,其中对角线BD与AC交于点O,BD=6cm,则对角线AC的长度是( )
A、 与 垂直 B、 C、 平分 D、若 的周长为4,则平行四边形 的周长为87. 如图,四边形ABCD是边长为5cm的菱形,其中对角线BD与AC交于点O,BD=6cm,则对角线AC的长度是( )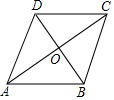 A、8cm B、4cm C、3cm D、6cm8. 直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k2x<k1x+b的解集为( )
A、8cm B、4cm C、3cm D、6cm8. 直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k2x<k1x+b的解集为( ) A、x<﹣1 B、x>﹣1 C、x>2 D、x<29. 如图,用一条宽相等的足够长的纸条,打一个结,如图(1)所示,然后轻轻拉紧、压平就可以得到如图(2)所示的正五边形ABCDE,则∠BAC=( ).
A、x<﹣1 B、x>﹣1 C、x>2 D、x<29. 如图,用一条宽相等的足够长的纸条,打一个结,如图(1)所示,然后轻轻拉紧、压平就可以得到如图(2)所示的正五边形ABCDE,则∠BAC=( ).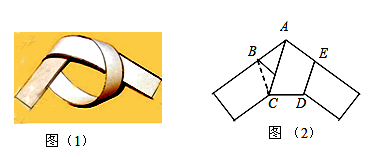 A、30° B、36° C、40° D、72°10. 如图,矩形 的面积为28,对角线交于点O;以 、 为邻边作平行四边形 ,对角线交于点 ;以 、 为邻边作平行四边形 ;…依此类推,则平行四边形 的面积为( )
A、30° B、36° C、40° D、72°10. 如图,矩形 的面积为28,对角线交于点O;以 、 为邻边作平行四边形 ,对角线交于点 ;以 、 为邻边作平行四边形 ;…依此类推,则平行四边形 的面积为( )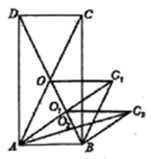 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 分式 与 的最简公分母是 .12. 若分式方程 有增根,则 的值是13. 如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=4,BC=10,则EF的长为 .
 14. 如图,在 中, 平分 交 于点E, ,垂足为F.若 ,则 等于.
14. 如图,在 中, 平分 交 于点E, ,垂足为F.若 ,则 等于.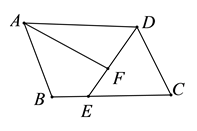 15. 如图,在菱形ABCD中,AB=18cm,∠A=60°,点E以2cm/s的速度沿AB边由A向B匀速运动,同时点F以4cm/s的速度沿CB边由C向B运动,F到达点B时两点同时停止运动.当点E运动秒时,△DEF为等边三角形.
15. 如图,在菱形ABCD中,AB=18cm,∠A=60°,点E以2cm/s的速度沿AB边由A向B匀速运动,同时点F以4cm/s的速度沿CB边由C向B运动,F到达点B时两点同时停止运动.当点E运动秒时,△DEF为等边三角形.
三、解答题
-
16. 计算(1)、因式分解:(2)、化简:(3)、解不等式组,并把解集在数轴上表示出来:(4)、解分式方程:17. 先化简,再求值: ,其中 .18. 如图,已知 的边 在直线 上,若将 绕点A按逆时针方向旋转,使点C落在直线 上的 处,得到 .
 (1)、请用尺规作图作出 ,并标明字母;(保留作图痕迹,不写作法)(2)、若角 ,则 .19. 数学课后,小玲和同桌小娟各自拿出自己的漂亮的正方形手帕,她们俩各有一条方格手帕和一条绣花手帕,如图,小玲说:“我的方格手帕的边长比你的方格手帕的边长大0.6 .”小娟说:“我的绣花手帕的边长比你的绣花手帕的边长大0.6 .”设小玲的两块手帕的面积和为 ,小娟的两块手帕的面积和为 ,请同学们运用因式分解的方法算一算 与 的差.
(1)、请用尺规作图作出 ,并标明字母;(保留作图痕迹,不写作法)(2)、若角 ,则 .19. 数学课后,小玲和同桌小娟各自拿出自己的漂亮的正方形手帕,她们俩各有一条方格手帕和一条绣花手帕,如图,小玲说:“我的方格手帕的边长比你的方格手帕的边长大0.6 .”小娟说:“我的绣花手帕的边长比你的绣花手帕的边长大0.6 .”设小玲的两块手帕的面积和为 ,小娟的两块手帕的面积和为 ,请同学们运用因式分解的方法算一算 与 的差.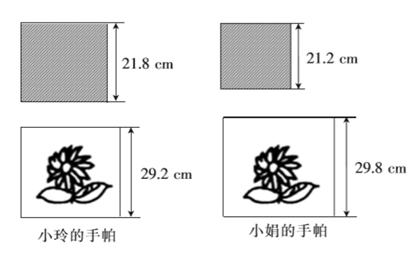 20. 如图,在四边形 中, , 与 交于点E , E是 的中点,延长 到点F , 使 ,连接 .
20. 如图,在四边形 中, , 与 交于点E , E是 的中点,延长 到点F , 使 ,连接 .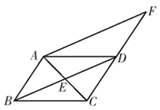 (1)、求证: .(2)、求证:四边形 是平行四边形.21. 面对新冠肺炎疫情带来的挑战,党中央全面部署疫情防控和经济社会发展重点工作,复工复产按下“快进”键,全国掀起了“为‘鄂’拼单”的热潮.某特产超市看准商机,用10000元购进一批湖北特产玉露茶,销量可观,于是又用18000元购进一批同款规格的玉露茶,但第二次进价比第一次每盒下降10元,第二次所购进数量恰好是第一次数量的2倍.(1)、求第一次购进玉露茶时每盒的价格;(2)、已知该超市第一批玉露茶在进价基础上提高50%出售.若要保证售完这两批玉露茶的获利不低于11000元,则第二批玉露茶每盒的售价至少应为多少元?22. 阅读下列材料:通过小学的学习我们知道,分数可分为“真分数”和“假分数”.而假分数都可化为带分数,如: .我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.如: , 这样的分式就是假分式;再如: , 这样的分式就是真分式.类似的,假分式也可以化为带分式(即:整式与真分式的和的形式).如: ;再如: .
(1)、求证: .(2)、求证:四边形 是平行四边形.21. 面对新冠肺炎疫情带来的挑战,党中央全面部署疫情防控和经济社会发展重点工作,复工复产按下“快进”键,全国掀起了“为‘鄂’拼单”的热潮.某特产超市看准商机,用10000元购进一批湖北特产玉露茶,销量可观,于是又用18000元购进一批同款规格的玉露茶,但第二次进价比第一次每盒下降10元,第二次所购进数量恰好是第一次数量的2倍.(1)、求第一次购进玉露茶时每盒的价格;(2)、已知该超市第一批玉露茶在进价基础上提高50%出售.若要保证售完这两批玉露茶的获利不低于11000元,则第二批玉露茶每盒的售价至少应为多少元?22. 阅读下列材料:通过小学的学习我们知道,分数可分为“真分数”和“假分数”.而假分数都可化为带分数,如: .我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.如: , 这样的分式就是假分式;再如: , 这样的分式就是真分式.类似的,假分式也可以化为带分式(即:整式与真分式的和的形式).如: ;再如: .解决下列问题:
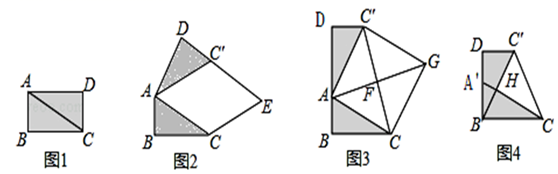
(1)、分式 是分式(填“真分式”或“假分式”);(2)、把假分式 化为带分式的形式(写出过程);(3)、如果分式 的值为整数,那么x的整数值为 .23. (问题情境):在综合与实践课上,老师让同学们以“矩形纸片的剪拼”为主题开展数学活动.如图1,将矩形纸片ABCD沿对角线AC剪开,得到△ABC和△ACD.并且量得AB=2cm,AC=4cm.
 (1)、(操作发现):
(1)、(操作发现):将图1中的△ACD以点A为旋转中心,按逆时针方向旋转∠α,使∠α=∠BAC,得到如图2所示的△AC′D,过点C作AC′的平行线,与DC′的延长线交于点E,则以点A、C、E、C′为顶点的四边形是什么特殊四边形?并说明理由.
(2)、创新小组将图1中的△ACD以点A为旋转中心,按逆时针方向旋转,使B、A、D三点在同一条直线上,得到如图3所示的△AC′D,连接CC′,取CC′的中点F,连接AF并延长至点G,使FG=AF,连接CG、C′G,得到四边形ACGC′,发现它是正方形,请你证明这个结论.(3)、(实践探究):缜密小组在创新小组发现结论的基础上,进行如下操作:将△ABC沿着BD方向平移,使点B与点A重合,此时A点平移至A′点,A′C与BC′相交于点H,如图4所示,连接CC′,直接写出 的值.