山西省大同市灵丘县2019-2020学年八年级下学期数学期末试卷

试卷更新日期：2021-04-23 类型：期末考试

进入出卷网下载

一、单选题

1. 下列运算正确的是（　　）

A、 $\sqrt{36}$ =±6 B、4 $\sqrt{3}$ ﹣3 $\sqrt{3}$ =1 C、 $\sqrt{12} \div \sqrt{2}$ =6 D、 $\sqrt{\frac{3}{2}} \times \sqrt{24}$ =6

查看试题解析
2. 以下列各组数为边长，不能构成直角三角形的是（）

A、5，12，13 B、1，2， $\sqrt{5}$ C、1， $\sqrt{3}$ ，2 D、4，5，6

查看试题解析
3. 下列命题中，是真命题的是（）

A、两条对角线互相平分的四边形是平行四边形 B、两条对角线相等的四边形是矩形 C、两条对角线互相垂直的四边形是菱形 D、两条对角线互相垂直且相等的四边形是正方形

查看试题解析
4. 如图，两把完全一样的直尺叠放在一起，重合的部分构成一个四边形，这个四边形一定是（）

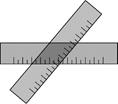A、矩形 B、菱形 C、正方形 D、无法判断

查看试题解析
5. 下列函数的图象不经过第一象限，且y随x的增大而减小的是（）

A、 $y = - x$ B、 $y = x + 1$ C、 $y = - 2 x + 1$ D、 $y = x - 1$

查看试题解析
6. 为了调查某校同学的体质健康状况，随机抽查了若干名同学的每天锻炼时间如表：

每天锻炼时间（分钟）

20

40

60

90

学生数

2

3

4

1

则关于这些同学的每天锻炼时间，下列说法错误的是（）

A、众数是60 B、平均数是21 C、抽查了10个同学 D、中位数是50

查看试题解析
7. 如图， $▱ A B C D$ 中，AC．BD为对角线，BC=3，BC边上的高为2，则阴影部分的面积为（　　）

A、3 B、6 C、12 D、24

查看试题解析
8. 如图，在菱形ABCD中，AB＝6，∠ABC＝60°，M为AD中点，P为对角线BD上一动点，连接PA和PM，则PA＋PM的最小值是（）

A、3 B、2 $\sqrt{3}$ C、3 $\sqrt{3}$ D、6

查看试题解析
9. 将矩形纸片ABCD按如图所示的方式折叠，得到菱形AECF．若AB=6，则BC的长为（）．

A、3 B、3 $\sqrt{2}$ C、2 $\sqrt{3}$ D、 $\frac{3 \sqrt{2}}{2}$

查看试题解析
10. 如图，把Rt△ABC放在直角坐标系内，其中∠CAB=90°，BC=10，点A、B的坐标分别为（2，0）、（8，0），将△ABC沿x轴向右平移，当点C落在直线y=x﹣5上时，线段BC扫过的面积为（）．

A、80 B、88 C、96 D、100

查看试题解析

二、填空题

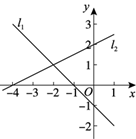
11. 函数y= $\sqrt{3 - x} + \frac{1}{x - 2}$ 中自变量x的取值范围是

查看试题解析
12. 有一个三角形两边长为3和4，要使该三角形为直角三角形，则第三边长为

查看试题解析
13. 如图，在平面直角坐标系xOy中，直线 $l_{1}$ ， $l_{2}$ 分别是函数 $y = k_{1} x + b_{1}$ 和 $y = k_{2} x + b_{2}$ 的图象，则可以估计关于x的不等式 $k_{1} x + b_{1} > k_{2} x + b_{2}$ 的解集为．

查看试题解析
14. 如图，在正方形ABCD中，点D的坐标是（0，1），点A的坐标是（-2，2），则点B的坐标为．

查看试题解析
15. 如图，点A，B，E在同一条直线上，正方形ABCD，BEFG的边长分别为3，4，H为线段DF的中点，则BH= ．

查看试题解析

三、解答题

16. 计算：

(1)、（ $\sqrt{8}$ － $\sqrt{2}$ ）× $\sqrt{\frac{1}{2}}$ ．

(2)、化简 $\sqrt{a^{2} - 4 a + 4}$ ＋|a﹣1|，其中1＜a＜ $\sqrt{2}$ ．

查看试题解析
17. 如图，在Rt△ABC中，∠C=90°，以AC为一边向外作等边三角形ACD，点E为AB的中点，连结DE．

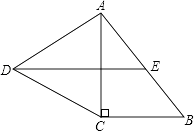(1)、证明DE∥CB；

(2)、探索AC与AB满足怎样的数量关系时，四边形DCBE是平行四边形．

查看试题解析
18. 小泽和小帅两同学分别从甲地出发，骑自行车沿同一条路到乙地参加社会实践活动．如图折线OAB和线段CD分别表示小泽和小帅离甲地的距离y（单位：千米）与时间x（单位：小时）之间函数关系的图象．根据图中提供的信息，解答下列问题：

(1)、小帅的骑车速度为千米/小时；点C的坐标为；

(2)、求线段AB对应的函数表达式；

(3)、当小帅到达乙地时，小泽距乙地还有多远？

查看试题解析

19. 某班在一次班会课上，就“遇见路人摔倒后如何处理”的主题进行讨论，并对全班 50 名学生的处理方式进行统计，得出相关统计表和统计图．

组别	A	B	C	D
处理方式	迅速离开	马上救助	视情况而定	只看热闹
人数	m	30	n	5

请根据表图所提供的信息回答下列问题：

(1)、统计表中的 m＝， n＝；

(2)、补全频数分布直方图；

(3)、若该校有 2000 名学生，请据此估计该校学生采取“马上救助”方式的学生有多少人？

查看试题解析

20. 如图，在平面直角坐标系xOy中，直线 $l$ 的表达式为 $y = 2 x - 6$ ，点A ， B的坐标分别为（1，0），（0，2），直线AB与直线 $l$ 相交于点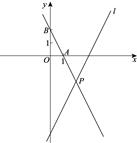P ．

(1)、求直线AB的表达式；

(2)、求点P的坐标；

(3)、若直线 $l$ 上存在一点C ，使得△APC的面积是△APO的面积的2倍，直接写出点C的坐标．

查看试题解析
21. 已知：如图已知直线 $A B$ 的函数解析式为 $y = - 2 x + 8$ ，与x轴交于点A，与y轴交于点B．

(1)、求A、B两点的坐标；

(2)、若点 $P (m ， n)$ 为线段 $A B$ 上的一个动点（与A、B不重合），作 $P E ⊥ x$ 轴于点E， $P F ⊥ y$ 轴于点F，连接 $E F$ ，问：
①若 $△ P A O$ 的面积为S，求S关于m的函数关系式，并写出m的取值范围；

②是否存在点P，使 $E F$ 的值最小？若存在，求出 $E F$ 的最小值；若不存在，请说明理由．

查看试题解析
22. 某公司销售部有营业员15人，该公司为了调动营业员的积极性，决定实行目标管理，根据目标完成的情况对营业员进行适当的奖励，为了确定一个适当的月销售目标，公司有关部门统计了这15人某月的销售量，如下表所示：

月销售量/件数

1770

480

220

180

120

90

人数

1

1

3

3

3

4

(1)、直接写出这15名营业员该月销售量数据的平均数、中位数、众数；

(2)、如果想让一半左右的营业员都能达到月销售目标，你认为(1)中的平均数、中位数、众数中，哪个最适合作为月销售目标？请说明理由.

查看试题解析
23. 在图1，2，3中，已知 $▱ A B C D$ ， $∠ A B C = 120^{°}$ ，点E为线段 $B C$ 上的动点，连接 $A E$ ，以 $A E$ 为边向上作菱形 $A E F G$ ，且 $∠ E A G = 120^{°}$ ．

(1)、如图1，当点E与点B重合时， $∠ C E F =$ °；

(2)、如图2，连接 $A F$ ．
①填空： $∠ F A D$ ▲ $∠ E A B$ （填“>”，“<”，“=”）；

②求证：点F在 $∠ A B C$ 的平分线上；

(3)、如图3，连接 $E G$ ， $D G$ ，并延长 $D G$ 交 $B A$ 的延长线于点H，当四边形 $A E G H$ 是平行四边形时，求 $\frac{B C}{A B}$ 的值．

查看试题解析

每天锻炼时间（分钟）	20	40	60	90
学生数	2	3	4	1

月销售量/件数	1770	480	220	180	120	90
人数	1	1	3	3	3	4