河北省唐山市路南区2018-2019学年八年级下学期数学期末试卷
试卷更新日期:2021-04-23 类型:期末考试
一、单选题
-
1. 等于( )A、 B、 C、 D、2. 函数 中,自变量x的取值范围是( )A、 B、 C、 D、3. 已知一个表面积为 的正方体,这个正方体的棱长为( )A、 B、 C、 D、4. 四边形的三个相邻内角的度数依次如下,那么其中是平行四边形的为( )A、 , , B、 , , C、 , , D、 , ,5. 实数a,b在数轴上对应点的位置如图所示,化简 |a| + 的结果是( )
 A、-2a + b B、2a-b C、-b D、b6. 如图,为测量位于一水塘旁的两点A,B间的距离,在地面上确定点O,分别取 , 的中点C,D,量得 ,则A,B之间的距离为( )
A、-2a + b B、2a-b C、-b D、b6. 如图,为测量位于一水塘旁的两点A,B间的距离,在地面上确定点O,分别取 , 的中点C,D,量得 ,则A,B之间的距离为( ) A、 B、 C、 D、7. 如图,将正方形OABC放在平面直角坐标系中,O是原点,点A的坐标为(1, ),则点C的坐标为( )
A、 B、 C、 D、7. 如图,将正方形OABC放在平面直角坐标系中,O是原点,点A的坐标为(1, ),则点C的坐标为( )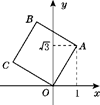 A、(- ,1) B、(-1, ) C、( ,1) D、(- ,-1)8. 我校四名跳远运动员之前的10次跳远测试中成绩的平均数相同,方差s2如表所示,如果要选出一名跳远成绩最稳定的选手参加抚顺市运动会,应选择的选手是( )
A、(- ,1) B、(-1, ) C、( ,1) D、(- ,-1)8. 我校四名跳远运动员之前的10次跳远测试中成绩的平均数相同,方差s2如表所示,如果要选出一名跳远成绩最稳定的选手参加抚顺市运动会,应选择的选手是( )选手
甲
乙
丙
丁
s2
0.5
0.5
0.6
0.4
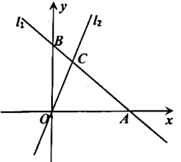
A、甲 B、乙 C、丙 D、丁9. 已知汽车油箱内有油40L,每行驶100km耗油10L,则汽车行驶过程中油箱内剩余的油量Q (L)与行驶路程s(km)之间的函数表达式是( )A、Q=40+ B、Q=40﹣ C、Q=40﹣ D、Q=40+10. 如图,在菱形 中, , ,O为对角线 的中点,过O点作 ,垂足为E.则下列说法错误的是( )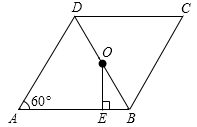 A、点O为菱形 的对称中心 B、 C、 为等边三角形 D、11. 已知,y与 成正比例,且比例系数为 ,则当 时,x的值为( )A、 B、 C、 D、12. 如图,在平面直角坐标系中, 的顶点坐标分别为 , , ,当直线 与 有交点时,k的取值范围是( )
A、点O为菱形 的对称中心 B、 C、 为等边三角形 D、11. 已知,y与 成正比例,且比例系数为 ,则当 时,x的值为( )A、 B、 C、 D、12. 如图,在平面直角坐标系中, 的顶点坐标分别为 , , ,当直线 与 有交点时,k的取值范围是( )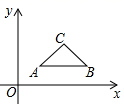 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 一组数据 的平均数是14. 若一次函数 的图象经过第二、三、四象限,则m的取值范围是 .15. 如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG,若AD=5,DE=6,则AG的长是 .
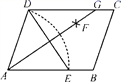 16. 如图,在直角△OAB中,∠AOB=30°,将△OAB绕点O逆时针旋转100°得到△OA1B1 , 则∠A1OB=°.
16. 如图,在直角△OAB中,∠AOB=30°,将△OAB绕点O逆时针旋转100°得到△OA1B1 , 则∠A1OB=°.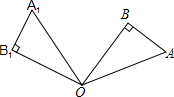 17. 已知实数m,n满足 ,则 .18. 如图,一个函数的图象由射线 ,线段 ,射线 组成,其中点 , , , .当y随x的增大而增大时,则x的取值范围是 .
17. 已知实数m,n满足 ,则 .18. 如图,一个函数的图象由射线 ,线段 ,射线 组成,其中点 , , , .当y随x的增大而增大时,则x的取值范围是 .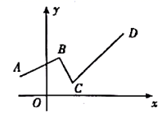
三、解答题
-
19. 计算:(1)、(2)、20. 根据下列要求,完成解答.
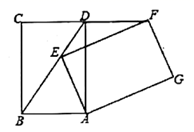
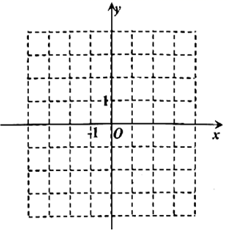 (1)、列表如下,在所给坐标系中,画出函数 的图象.(2)、判断点 , 是否在函数 的图象上?(3)、若点 在函数 的图象上,求出m的值.21. 如图, 的周长是 ,对角线 与 交于点O, 于点A,点E是 中点, 的周长比 的周长多 .
(1)、列表如下,在所给坐标系中,画出函数 的图象.(2)、判断点 , 是否在函数 的图象上?(3)、若点 在函数 的图象上,求出m的值.21. 如图, 的周长是 ,对角线 与 交于点O, 于点A,点E是 中点, 的周长比 的周长多 .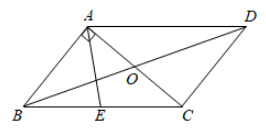 (1)、求边 、 的长;(2)、求 的长度;(3)、求 的面积.22. 一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.两车同时出发,设慢车行驶的时间为 ,两车之间的距离为 ,图中的折线表示y与x之间的函数关系,根据图象回答以下问题:
(1)、求边 、 的长;(2)、求 的长度;(3)、求 的面积.22. 一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.两车同时出发,设慢车行驶的时间为 ,两车之间的距离为 ,图中的折线表示y与x之间的函数关系,根据图象回答以下问题: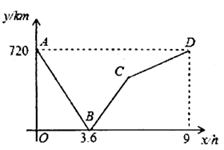 (1)、两车的速度和为 ;(2)、当 h时,两车相遇;(3)、最先到达的是车;图中点C的实际意义为;(4)、快车用 行驶的距离与慢车行驶h的距离相等;(5)、当两车的距离为 ,会有个时刻?23. 某厂为了解工人在单位时间内加工同一种零件的技能水平,随机抽取了 名工人加工的零件进行检测,统计出他们各自加工的合格品数是 到 这八个整数,现提供统计图的部分信息如图,请解答下列问题:
(1)、两车的速度和为 ;(2)、当 h时,两车相遇;(3)、最先到达的是车;图中点C的实际意义为;(4)、快车用 行驶的距离与慢车行驶h的距离相等;(5)、当两车的距离为 ,会有个时刻?23. 某厂为了解工人在单位时间内加工同一种零件的技能水平,随机抽取了 名工人加工的零件进行检测,统计出他们各自加工的合格品数是 到 这八个整数,现提供统计图的部分信息如图,请解答下列问题: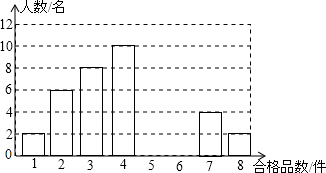 (1)、这 名工人加工出的合格品数的中位数为;(2)、如果合格品数分别为 、 的人数都不会超过 人,小刘同学说:这 名工人加工出合格品数的众数的取值一定会在 、 、 中产生.你认为小刘说法正确吗?;会同时是 、 、 三个吗?(3)、厂方认定,工人在单位时间内加工出的合格品数不低于 件为技能合格,否则,将接受技能再培训.已知该厂有同类工人 名,请估计该厂将接受技能再培训的人数.
(1)、这 名工人加工出的合格品数的中位数为;(2)、如果合格品数分别为 、 的人数都不会超过 人,小刘同学说:这 名工人加工出合格品数的众数的取值一定会在 、 、 中产生.你认为小刘说法正确吗?;会同时是 、 、 三个吗?(3)、厂方认定,工人在单位时间内加工出的合格品数不低于 件为技能合格,否则,将接受技能再培训.已知该厂有同类工人 名,请估计该厂将接受技能再培训的人数.