河北省唐山市古冶区2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2021-04-23 类型:期末考试
一、单选题
-
1. 下列图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列运算错误的是( )A、 B、 C、 D、3. 下列二次根式是最简二次根式的是( )A、 B、 C、 D、4. 平行四边形的一个内角为 ,与它相邻的另一个内角等于( )A、 B、 C、 D、5. 甲和乙一起练习射击,第一轮10枪打完后两人的成绩如图所示.设他们这10次射击成绩的方差为 、 ,下列关系正确的是( )
2. 下列运算错误的是( )A、 B、 C、 D、3. 下列二次根式是最简二次根式的是( )A、 B、 C、 D、4. 平行四边形的一个内角为 ,与它相邻的另一个内角等于( )A、 B、 C、 D、5. 甲和乙一起练习射击,第一轮10枪打完后两人的成绩如图所示.设他们这10次射击成绩的方差为 、 ,下列关系正确的是( ) A、 B、 C、 D、无法确定6. 已知点 和点 是正比例函数 图象上的两点,则a与b的大小关系是( )A、 B、 C、 D、以上都不对7. 某公司10名职工的5月份工资统计如下,该公司10名职工5月份工资的众数和中位数分别是( )
A、 B、 C、 D、无法确定6. 已知点 和点 是正比例函数 图象上的两点,则a与b的大小关系是( )A、 B、 C、 D、以上都不对7. 某公司10名职工的5月份工资统计如下,该公司10名职工5月份工资的众数和中位数分别是( )工资(元)
2000
2200
2400
2600
人数(人)
1
3
4
2
A、2400元、2400元 B、2400元、2300元 C、2200元、2200元 D、2200元、2300元8. 已知在平面直角坐标系 中,点 ,点B在直线 上,则 两点间的最小距离是( )A、1 B、 C、2 D、49. 现有两根铁棒,它们的长分别为2米和3米,如果想焊接一个直角三角形铁架,那么第三根铁棒的长为( )A、 米 B、5米 C、 米 D、 米或 米10. 菱形ABCD的对角线AC=6,BD=8,那么边AB的长度 是( )A、10 B、5 C、 D、11. 如图,在△ABC中,D、E分别是AB、AC的中点,AC=8,F是DE上一点,连接AF,CF,DF=1,若∠AFC=90°,则BC的长度为( ) A、10 B、12 C、14 D、1612. 甲乙两城市相距600千米,一辆货车和一辆客车均从甲城市出发匀速行驶至乙城市.已知货车出发1小时后客车再出发,先到终点的车辆原地休息.在汽车行驶过程中,设两车之间的距离为s(千米),客车出发的时间为t(小时),它们之间的关系如图所示,则下列结论错误的是( )
A、10 B、12 C、14 D、1612. 甲乙两城市相距600千米,一辆货车和一辆客车均从甲城市出发匀速行驶至乙城市.已知货车出发1小时后客车再出发,先到终点的车辆原地休息.在汽车行驶过程中,设两车之间的距离为s(千米),客车出发的时间为t(小时),它们之间的关系如图所示,则下列结论错误的是( ) A、货车的速度是60千米/小时 B、离开出发地后,两车第一次相遇时,距离出发地150千米 C、货车从出发地到终点共用时7小时 D、客车到达终点时,两车相距180千米
A、货车的速度是60千米/小时 B、离开出发地后,两车第一次相遇时,距离出发地150千米 C、货车从出发地到终点共用时7小时 D、客车到达终点时,两车相距180千米二、填空题
-
13. 化简=
14. 若直角三角形的两直角边的长分别为a、b,且满足 ,则该直角三角形的斜边长为 .15. 将一次函数 的图象向上平移3个单位,所得的直线不经过第象限.16. 如图,在 中, ,将 绕点A顺时针旋转 后得到 (点B的对应点是 ,点 的对应点是 ),连接 .若 ,则 . 17. 甲、乙、丙、丁四位同学五次数学测验成绩统计如表.如果从这四位同学中,选出一位成绩较好且状态稳定的同学参加全国数学联赛,那么应选 同学.
17. 甲、乙、丙、丁四位同学五次数学测验成绩统计如表.如果从这四位同学中,选出一位成绩较好且状态稳定的同学参加全国数学联赛,那么应选 同学.甲
乙
丙
丁
平均数
80
85
85
80
方 差
42
42
54
59
18. 在数学课上,老师提出问题:如图,将锐角三角形纸片 经过两次折叠,得到边 上的点 ,使得四边形 恰好为菱形.小明给出的折叠方法:如图,① 边向 边折叠,使 边落在 边上,得到折痕交 于D;②C点向 边折叠,使C点与D点重合,得到折痕交 边于E,交 边于F.老师说:“小明的作法正确.”请回答:小明这样折叠的依据是①是平行四边形;②是菱形.
三、解答题
-
19. 如图,每个小方格都是边长为1的正方形.
 (1)、可得 是直角三角形,请你说明理由:(2)、 的周长为 , 面积为 .20. 在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系, 的顶点都在格点上,
(1)、可得 是直角三角形,请你说明理由:(2)、 的周长为 , 面积为 .20. 在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系, 的顶点都在格点上,
⑴将 绕点O顺时针旋转 得到的 ,写出点 和 的坐标;
⑵将 绕点O逆时针旋转 得到的 ,写出点 和 的坐标;
⑶已知 关于直线l对称的 的顶点 的坐标为 ,请直接写出直线l的函数解析式.
21. 李伯种植了100棵樱桃树,为了估计今年樱桃的收入情况,到收获时,从中随机选取了20棵树的樱桃采摘,并将采摘的情况绘制了条形统计图如下,请你根据这幅统计图中给出的信息回答下面的问题:樱桃重量(千克/每棵)
12
15
16
18
20
22
24
25
树的棵数
1
1
2
3
3
1
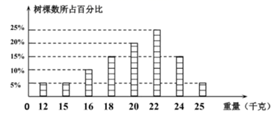 (1)、这20棵樱桃树所摘樱桃的平均重量为千克;(2)、这20棵樱桃树所摘樱桃重量的中位数是千克,众数是千克;(3)、请在以上平均数、中位数、众数三个数中,选择一个能更好地反映一棵樱桃树所摘樱桃重量平均水平的量,当每千克樱桃的批发价为12元,请估计李伯今年樱桃销售的总收入为多少元?22. 如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,分别过点A,C作AE∥DC,CE∥AB,两线交于点E.
(1)、这20棵樱桃树所摘樱桃的平均重量为千克;(2)、这20棵樱桃树所摘樱桃重量的中位数是千克,众数是千克;(3)、请在以上平均数、中位数、众数三个数中,选择一个能更好地反映一棵樱桃树所摘樱桃重量平均水平的量,当每千克樱桃的批发价为12元,请估计李伯今年樱桃销售的总收入为多少元?22. 如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,分别过点A,C作AE∥DC,CE∥AB,两线交于点E. (1)、求证:四边形AECD是菱形;(2)、如果∠B=60°,BC=2,求四边形AECD的面积.23. 在一段时间,某地区一种食品的需求量 (万斤)、供应量 (万斤)与价格x(元/斤)分别近似满足下列函数关系式: , .当需求量为0时,即停止供应.当 时,该食品的价格称为稳定价格,需求量称为稳定需求量.
(1)、求证:四边形AECD是菱形;(2)、如果∠B=60°,BC=2,求四边形AECD的面积.23. 在一段时间,某地区一种食品的需求量 (万斤)、供应量 (万斤)与价格x(元/斤)分别近似满足下列函数关系式: , .当需求量为0时,即停止供应.当 时,该食品的价格称为稳定价格,需求量称为稳定需求量. (1)、求该食品的稳定价格与稳定需求量;(2)、当价格x在范围时,该商品的需求量低于供应量;(3)、当供应量低于需求量时,政府常通过对供应方提供价格补贴来提高供货量.当供应量降低到20万斤时,为使该食品达到稳定价格,政府每斤应补贴多少元?24. 如图,在平面直角坐标系中,点O是坐标原点,四边形 是菱形,点A的坐标为 ,点C在x轴的正半轴上,直线 交y轴于点M, 边交y轴于点H,连接 .
(1)、求该食品的稳定价格与稳定需求量;(2)、当价格x在范围时,该商品的需求量低于供应量;(3)、当供应量低于需求量时,政府常通过对供应方提供价格补贴来提高供货量.当供应量降低到20万斤时,为使该食品达到稳定价格,政府每斤应补贴多少元?24. 如图,在平面直角坐标系中,点O是坐标原点,四边形 是菱形,点A的坐标为 ,点C在x轴的正半轴上,直线 交y轴于点M, 边交y轴于点H,连接 . (1)、菱形 的边长是;(2)、求直线 的解析式;(3)、动点P从点A出发,沿折线 方向以2个单位/秒的速度向终点C匀速运动,设 的面积为 ,点P的运动时间为t秒,当点P在 边上运动时,求S与t间的函数关系式.25. 如图,已知 是等腰直角三角形, ,点D是 的中点.作正方形 ,使点A、C分别在边 和 上,连接 , .
(1)、菱形 的边长是;(2)、求直线 的解析式;(3)、动点P从点A出发,沿折线 方向以2个单位/秒的速度向终点C匀速运动,设 的面积为 ,点P的运动时间为t秒,当点P在 边上运动时,求S与t间的函数关系式.25. 如图,已知 是等腰直角三角形, ,点D是 的中点.作正方形 ,使点A、C分别在边 和 上,连接 , . (1)、猜想线段 和 的数量关系是;(2)、将正方形 绕点D逆时针方向旋转 .判断(1)中的结论是否仍然成立?请利用图证明你的结论;
(1)、猜想线段 和 的数量关系是;(2)、将正方形 绕点D逆时针方向旋转 .判断(1)中的结论是否仍然成立?请利用图证明你的结论;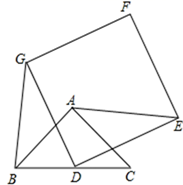 (3)、在(2)的条件下,若 ,当 时,直接写出 的值.
(3)、在(2)的条件下,若 ,当 时,直接写出 的值.