河北省衡水市景县2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2021-04-23 类型:期末考试
一、单选题
-
1. 若 ,则化简二次根式 的符合题意结果是( )A、 B、 C、 D、2. 若关于x的方程 有增根,则m的值是( )A、3 B、2 C、1 D、-13. 如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=6,BC=10,则EF的长为( )
 A、1 B、2 C、3 D、54. 将一根 24cm 的筷子,置于底面直径为 15cm , 高 8cm 的装满水的无盖圆柱形水杯中,设筷子浸没在杯子里面的长度为 hcm , 则 h 的取值范围是( )A、h≤15cm B、h≥8cm C、8cm≤h≤17cm D、7cm≤h≤16cm5. 如图,以Rt△ABC的三边为直角边分别向外作等腰直角三角形.若AB= ,则图中阴影部分的面积为( )
A、1 B、2 C、3 D、54. 将一根 24cm 的筷子,置于底面直径为 15cm , 高 8cm 的装满水的无盖圆柱形水杯中,设筷子浸没在杯子里面的长度为 hcm , 则 h 的取值范围是( )A、h≤15cm B、h≥8cm C、8cm≤h≤17cm D、7cm≤h≤16cm5. 如图,以Rt△ABC的三边为直角边分别向外作等腰直角三角形.若AB= ,则图中阴影部分的面积为( ) A、 B、 C、 D、56. 如图,正方体的棱长为4cm,A是正方体的一个顶点,B是侧面正方形对角线的交点.一只蚂蚁在正方体的表面上爬行,从点A爬到点B的最短路径是( )
A、 B、 C、 D、56. 如图,正方体的棱长为4cm,A是正方体的一个顶点,B是侧面正方形对角线的交点.一只蚂蚁在正方体的表面上爬行,从点A爬到点B的最短路径是( )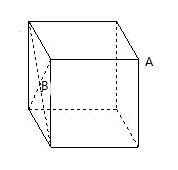 A、9 B、 C、 D、127. 如图,四边形 是菱形, , , 于点 .则 ( )
A、9 B、 C、 D、127. 如图,四边形 是菱形, , , 于点 .则 ( ) A、6 B、 C、 D、58. 某工厂一月份生产零件50万个,已知第一季度共生产零件182万个,若设该厂平均每月的增长率为x,可以列出方程( )A、 B、 C、 D、9. 在平面直角坐标系 中,点A,B在直线 上,且横坐标分别为1,2,过点A作AC⊥x轴于点C,过点B向y轴作垂线段,与直线 交于点D,若BD=OC,则下列结论一定成立的是( )A、 B、 C、 D、10. 正方形A1B1C1A2 , A2B2C2A3 , A3B3C3A4 , …,按如图所示的方式放置,点A1A2A3 , …和点B1B2B3 , …分别在直线y=x+1和x轴上.则点C2020的纵坐标是()
A、6 B、 C、 D、58. 某工厂一月份生产零件50万个,已知第一季度共生产零件182万个,若设该厂平均每月的增长率为x,可以列出方程( )A、 B、 C、 D、9. 在平面直角坐标系 中,点A,B在直线 上,且横坐标分别为1,2,过点A作AC⊥x轴于点C,过点B向y轴作垂线段,与直线 交于点D,若BD=OC,则下列结论一定成立的是( )A、 B、 C、 D、10. 正方形A1B1C1A2 , A2B2C2A3 , A3B3C3A4 , …,按如图所示的方式放置,点A1A2A3 , …和点B1B2B3 , …分别在直线y=x+1和x轴上.则点C2020的纵坐标是() A、22020 B、22019 C、22020 D、2201911. 如图,O是菱形ABCD的对角线AC、BD的交点,E、F分别是OA、OC的中点.下列结论:①S△ADE=S△EOD;②四边形BFDE也是菱形;③四边形ABCD的面积为EF×BD;④∠ADE=∠EDO;⑤△DEF是轴对称图形.其中正确的结论有( )
A、22020 B、22019 C、22020 D、2201911. 如图,O是菱形ABCD的对角线AC、BD的交点,E、F分别是OA、OC的中点.下列结论:①S△ADE=S△EOD;②四边形BFDE也是菱形;③四边形ABCD的面积为EF×BD;④∠ADE=∠EDO;⑤△DEF是轴对称图形.其中正确的结论有( )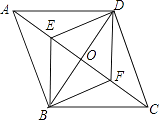 A、5个 B、4个 C、3个 D、2个
A、5个 B、4个 C、3个 D、2个二、填空题
-
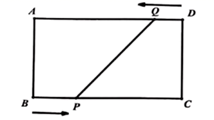
12. 已知一组数据a , b , c的方差为2,那么数据a+3,b+3,c+3的方差是 .13. 已知,在 中, ,且 边上的高为12,边BC的长为 .14. 在 中, , , ,斜边 的长为.15. 如图,在矩形 中, ,点 和点 分别从点 和点 同时出发,按逆时针方向沿矩形 的边运动,点 和点 的速度分别为 和 ,当四边形 初次为矩形时,点 和点 运动的时间为 .
三、解答题
-
16. 选用适当的方法解下列方程(1)、2x2﹣5x﹣8=0(2)、(x﹣2)(2x﹣3)=2(x﹣2)17. 为了了解某校2000名学生参加环保知识竞赛的成绩,从中抽取了部分学生的竞赛成绩(均为整数),整理后绘制成如下的频数分布直方图(如图),请结合图形解答下列问题.
 (1)、指出这个问题中的总体;(2)、求竞赛成绩在79.5~89.5这一小组的频率;(3)、如果竞赛成绩在90分以上(含90分)的同学可获得奖励,请估计全校约有多少人获得奖励.18. 某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.(1)、求每台A型电脑和B型电脑的销售利润;(2)、该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)、指出这个问题中的总体;(2)、求竞赛成绩在79.5~89.5这一小组的频率;(3)、如果竞赛成绩在90分以上(含90分)的同学可获得奖励,请估计全校约有多少人获得奖励.18. 某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.(1)、求每台A型电脑和B型电脑的销售利润;(2)、该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?最大利润是多少?
19. 如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与y轴交于点D,与正比例函数y=3x的图象相交于点C,点C的横坐标为1. (1)、求k,b的值;(2)、请直接写出不等式kx+b﹣3x>0的解集;(3)、M为射线CB上一点,过点M作y轴的平行线交y=3x于点N,当MN=OD时,求M点的坐标.20. 小明在学完了平行四边形这个章节后,想对“四边形的不稳定性”和“四边形的判定”有更好的理解,做了如下的探究:他将8个木棍和一些钉子组成了一个正方形 和平行四边形 (如图1),且 , 在一条直线上,点 落在边 上.经小明测量,发现此时 、 、 三个点在一条直线上, , .
(1)、求k,b的值;(2)、请直接写出不等式kx+b﹣3x>0的解集;(3)、M为射线CB上一点,过点M作y轴的平行线交y=3x于点N,当MN=OD时,求M点的坐标.20. 小明在学完了平行四边形这个章节后,想对“四边形的不稳定性”和“四边形的判定”有更好的理解,做了如下的探究:他将8个木棍和一些钉子组成了一个正方形 和平行四边形 (如图1),且 , 在一条直线上,点 落在边 上.经小明测量,发现此时 、 、 三个点在一条直线上, , . (1)、求 的长度;(2)、设 的长度为 , (用含 的代数式表示);(3)、小明接着探究,在保证 , 位置不变的前提条件下,从点 向右推动正方形,直到四边形 刚好变为矩形时停止推动(如图2).若此时 ,求 的长度.
(1)、求 的长度;(2)、设 的长度为 , (用含 的代数式表示);(3)、小明接着探究,在保证 , 位置不变的前提条件下,从点 向右推动正方形,直到四边形 刚好变为矩形时停止推动(如图2).若此时 ,求 的长度. 21. 如图, , , .动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l(其解析式为 ,且直线l与x轴所夹的锐角为45°)也随之移动,设移动时间为t秒.
21. 如图, , , .动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l(其解析式为 ,且直线l与x轴所夹的锐角为45°)也随之移动,设移动时间为t秒.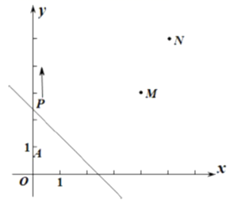 (1)、当 时,求l的解析式;(2)、若点M , N位于l的异侧,确定t的取值范围;(3)、求出t为何值时,点M关于l的对称点落在坐标轴上.22. 如图,正方形 的边 在坐标轴上,点B坐标为 ,将正方形 绕点C逆时针旋转角度 ,得到正方形 , 交线段 于点G, 的延长线交线段 于点H,连 .
(1)、当 时,求l的解析式;(2)、若点M , N位于l的异侧,确定t的取值范围;(3)、求出t为何值时,点M关于l的对称点落在坐标轴上.22. 如图,正方形 的边 在坐标轴上,点B坐标为 ,将正方形 绕点C逆时针旋转角度 ,得到正方形 , 交线段 于点G, 的延长线交线段 于点H,连 . (1)、求证: ;(2)、求 的度数;并判断线段 之间的数量关系,说明理由;(3)、连结 得到四边形 ,在旋转过程中,当G点在何位置时四边形 是矩形?请说明理由并求出点H的坐标.
(1)、求证: ;(2)、求 的度数;并判断线段 之间的数量关系,说明理由;(3)、连结 得到四边形 ,在旋转过程中,当G点在何位置时四边形 是矩形?请说明理由并求出点H的坐标.