河北省邯郸市永年区2019-2020学年八年级下学期数学期末试卷

试卷更新日期：2021-04-23 类型：期末考试

进入出卷网下载

一、单选题

1. 某班进行民主选举班干部，要求每位同学将自己心中认为最合适的一位侯选上，投入推荐箱．这个过程是收集数据中的（　　）

A、确定调查对象 B、展开调查 C、选择调查方法 D、得出结论

查看试题解析
2. 点A关于y轴的对称点 $A_{1}$ 坐标是 $(- 2, - 1)$ ，则点A的坐标是（）

A、 $(- 1, - 2)$ B、 $(2, 1)$ C、 $(- 2, 1)$ D、 $(2, - 1)$

查看试题解析
3. 如图，在 $△ A B C$ 中，D，E分别是 $A B$ ， $A C$ 的中点，则下列说法正确的是（）

A、 $A E = B D$ B、 $B D = D E$ C、 $∠ D E C + ∠ B = 180 °$ D、 $∠ B D E + ∠ B = 180 °$

查看试题解析
4. 已知 $A (- 1 ， y_{1})$ 和 $B (m, y_{2})$ 在一次函数 $y = - 3 x + b (b$ 为常数）的图象上，且 $y_{1} < y_{2}$ ，则 $m$ 的值可能是（）

A、 $- 2$ B、 $- 1$ C、 $0$ D、 $2$

查看试题解析
5. 菱形不具备的性质是（　　）

A、对角线一定相等 B、对角线互相垂直 C、是轴对称图形 D、是中心对称图形

查看试题解析
6. 国务院决定于2020年11月1日零时开展第七次全国人口普查，人口调查采用普查方式的理由是（）

A、人口调查的数目不太大 B、人口调查需要获得全面准确的信息 C、人口调查具有破坏性 D、受条件限制，无法进行抽样调查

查看试题解析
7. 下列各曲线中，不表示y是 x的函数的是（）

A、 B、 C、 D、

查看试题解析
8. 在平面直角坐标系中， $A (1 ， 2)$ ， $B (4 ， 6)$ ，若把线段 $A B$ 扩大 $2$ 倍得线段 $A^{'} B^{'}$ ，若 $A^{'} (2 ， 4)$ ，则 $B^{'}$ 的坐标可以是（）

A、 $(2 ， 3)$ B、 $(3 ， 2)$ C、 $(8 ， 12)$ D、 $(12 ， 8)$

查看试题解析
9. 若把钟面上的每个刻度均看作一个点，那么表示 $2$ 时的刻度在表示 $12$ 时的刻度的方向为（）

A、北偏东 $60 °$ B、北偏东 $30 °$ C、南偏东 $60 °$ D、南偏东 $30 °$

查看试题解析
10. 小磊利用所学的数学知识，给同伴出了这样一道题：如图，某人从点A出发，沿直线走 $5$ 米后，向左转 $θ$ ，接着沿左转后的方向前进 $5$ 米后，再向左转 $θ$ ，再沿左转后的方向前进 $5$ 米 $\dots$ $\dots$ 如此下去，当他第一次回到A点时，发现自己走了 $60$ 米，则 $θ$ 的度数为（）

A、 $28 °$ B、 $30 °$ C、 $33 °$ D、 $36 °$

查看试题解析
11. 若实数 $k$ 、 $b$ 满足 $k + b = 0$ ，且 $k > b$ ，则一次函数 $y = k x + b$ 的图象可能是（）

A、 B、 C、 D、

查看试题解析
12. 如图，是小垣同学某两天进行体育锻炼的时间统计图，第一天锻炼了1小时，第二天锻炼了40分钟，根据统计图，小垣这两天体育锻炼时间最长的项目是（）

A、跳绳 B、引体向上 C、跳远 D、仰卧起坐

查看试题解析
13. 把图1中的菱形沿对角线分成四个全等的直角三角形，将这四个直角三角形分别拼成如图2，图3所示的正方形，则图1中菱形的面积为（　　）

A、6 B、24 C、26 D、12

查看试题解析
14. 如图1，在矩形ABCD中，AB＜BC，点E为对角线AC上的一个动点，连接BE，DE，过E作EF⊥BC于F.设AE＝x，图1中某条线段的长为y，若表示y与x的函数关系的图象大致如图2所示，则这条线段可能是图1中的（）

A、线段BE B、线段EF C、线段CE D、线段DE

查看试题解析

二、填空题

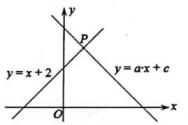
15. 在函数 $y = \frac{\sqrt{x}}{x - 1}$ 中，自变量x的取值范围是.

查看试题解析
16. 如图，直角坐标系中直线y=x+2和直线y=ax+c相交于点P(m，3)，则方程组 ${\begin{cases} y = x + 2 \\ y = a x + c \end{cases}$ 的解为。

查看试题解析
17. 如图，在平面直角坐标系中，点A，B的坐标分别为 $(- 1 ， 0)$ ， $(3 ， 0)$ ，现同时将点A，B分别向上平移 $2$ 个单位，再向右平移 $1$ 个单位，分别得到点A，B的对应点C，D，则D的坐标为，连接 $A C$ ， $B D$ ．在y轴上存在一点P，连接 $P A$ ， $P B$ ，使 $S_{Δ P A B} = S_{四边形 A B D C}$ ．则点P的坐标为．

查看试题解析

三、解答题

18. 研究发现，学生对概念的接受能力y与提出概念所用的时间x（分钟）之间有如下关系：

提出概念所用的时间x（分钟）	$2$	$5$	$7$	$10$	$12$	$13$	$14$	$17$	$20$
对概念的接受能力y	$47.8$	$53.5$	$56.3$	$59$	$59.8$	$59.9$	$59.8$	$58.3$	$55$

根据以上信息，回答下列问题：

(1)、当提出概念所用的时间为

10

分钟时，学生的接受能力约是多少？

(2)、当提出概念所用的时间为多少分钟时，学生的接受能力最强？

(3)、当

2 < x < 13

时，学生的接受能力随提出概念的时间增加而怎么样发生变化？当

13 < x < 20

时，学生的接受能力随提出概念的时间增加而怎么样发生变化？

查看试题解析

19. 如图，在边长为 $1$ 个单位长度的小正方形组成的网格中，小明家可用坐标 $(- 1 ， 2)$ 表示，汽车站可用坐标 $(3 ， - 1)$ 表示．

⑴建立平面直角坐标系，画出x轴和y轴；

⑵某星期日早晨，小明同学从家出发，沿 $(0 ， 1) \to (- 2 ， - 1) \to (- 1 ， - 2) \to (0 ， - 1) \to (1 ， 0) \to (2 ， - 1) \to (2 ， 2)$ 的路线转了一圈，又回到家里，写出他路上经过的地方．

查看试题解析
20. 如图，五边形ABCDE的内角都相等，EF平分∠AED ．求证：EF⊥BC ．

查看试题解析
21. 某校九年级学生共 $600$ 人，为了解这个年级学生的体能，从中随机抽取部分学生进行 $1$ 分钟的跳绳测试，并指定甲，乙，丙，丁四名同学对这次测试结果的数据作出整理，下面是这四名同学提供的部分信息：
甲：将全体测试数据分成 $6$ 组绘成直方图（如图）

乙：跳绳次数不少于 $105$ 次的同学占人数 $96 %$

丙：第①，②两组频率之和为 $0.12$ ，且第②组与第⑥组频数都是 $8$ ．

丁：第②，③，④组的频数之比为 $4 ： 17 ： 15$ ．

根据这四名同学提供的材料，请解答如下问题：

（每组数据含左端点值不含右端点值）

(1)、这次跳绳测试共抽取多少名学生？

(2)、如果跳绳次数不少于 $135$ 次为优秀，根据这次抽查的结果，估计全年级达到跳绳优秀的人数为多少？

查看试题解析
22. 如图，将平行四边形 $A B C O$ 放置在平面直角坐标系 $x O y$ 中，O为坐标原点，若点A的坐标是 $(6 ， 0)$ ，点C的坐标是 $(1 ， 4)$ ．

(1)、点B的坐标为；

(2)、求直线 $A C$ 的表达式；

(3)、若点C关于x轴的对称点为点E，设过点E的直线 $y = k x + b$ ，与四边形 $A B C O$ 有公共点，结合函数图象，求k的取值范围．

查看试题解析
23. 如图，AC为矩形ABCD的对角线，将边AB沿AE折叠，使点B落在AC上的点M处，将边CD沿CF折叠，使点D落在AC上的点N处．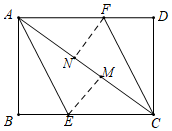

(1)、求证：四边形AECF是平行四边形；

(2)、当∠BAE为多少度时，四边形AECF是菱形？请说明理由．

查看试题解析
24. 某陶瓷公司生产茶壶和茶碗，一号窑炉每天生产 $100$ 把茶壶或和生产 $600$ 个茶碗；二号窑炉每天生产 $60$ 把茶壶或生产 $440$ 个茶碗．为了保证受热均匀，在一天当中，每个窑炉只生产茶壶或只生产茶碗．已知每把茶壶配 $6$ 个茶碗为一套茶具，每月按 $30$ 天计算，生产出的茶壶和茶碗正好配套，设一号窑炉生产茶壶x天，二号窑炉生产茶壶y天．

(1)、请你求出y与x之间的函数关系式；

(2)、设两个窑炉每月生产P套茶具．
①试求出P与x之间的函数关系式；

②当x为何值时，P取最小值，最小值是多少？

查看试题解析