河北省保定市阜平县2019-2020学年八年级下学期数学期末试卷

试卷更新日期：2021-04-23 类型：期末考试

进入出卷网下载

一、单选题

1. 要使二次根式 $\sqrt{2 x - 1}$ 有意义，字母x必须满足的条件是（　　）

A、 $x ⩽ \frac{1}{2}$ B、 $x < \frac{1}{2}$ C、 $x ⩾ \frac{1}{2}$ D、 $x > \frac{1}{2}$

查看试题解析
2. 在一次期末考试中，某一小组的6名同学的数学成绩（单位：分）分别是114，115，100，108，110，120，则这组数据的中位数是（　　）

A、100 B、108 C、112 D、120

查看试题解析
3. 四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是（）

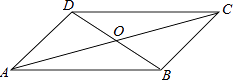A、AB∥DC，AD∥BC B、AB=DC，AD=BC C、AO=CO，BO=DO D、AB∥DC，AD=BC

查看试题解析
4. 计算 $\sqrt{18}$ ÷ $\sqrt{\frac{3}{4}}$ × $\sqrt{\frac{4}{3}}$ 结果为（）

A、3 $\sqrt{2}$ B、4 $\sqrt{2}$ C、5 $\sqrt{2}$ D、6 $\sqrt{2}$

查看试题解析
5. 一次函数 $y = - 3 x + 4$ 的图象不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
6. 已知，如图长方形ABCD中，AB=3cm，AD=9cm，将此长方形折叠，使点B与点D重合，折痕为EF，则△ABE的面积为（）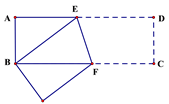

A、3cm² B、4cm² C、6cm² D、12cm²

查看试题解析
7. 有一个直角三角形的两边长分别为5和12，则第三边长为（）

A、13 B、 $\sqrt{119}$ C、13或 $\sqrt{119}$ D、无法确定

查看试题解析
8. 如图，已知四边形ABCD为菱形，AD＝5cm，BD＝6cm，则此菱形的面积为（）

A、12cm² B、24cm² C、48cm² D、96cm²

查看试题解析
9. 如图，矩形ABCD中，对角线AC、BD交于点O ．若∠AOB＝60°，BD＝10，则AB的长为（）

A、5 $\sqrt{3}$ B、5 C、4 D、3

查看试题解析
10. 如图，平行四边形 $A B C D$ 的周长为40， $Δ B O C$ 的周长比 $Δ A O B$ 的周长多10，则 $A B$ 为（）

A、5 B、20 C、10 D、15

查看试题解析
11. 已知一次函数y＝kx＋b的图像，如图所示，当x＜0时，y的取值范围是（）

A、y＞0 B、y＜0 C、－2＜y＜0 D、y＜－2

查看试题解析
12. 小李以每千克0.8元的价格从批发市场购进若干千克的西瓜到市场去销售，在销售了部分西瓜之后，余下的每千克降价0.4元，全部售完，销售金额与西瓜的千克数之间的关系如图所示，那么小李赚了（）

A、32元 B、36元 C、38元 D、44元

查看试题解析

二、填空题

13. 计算（ $\sqrt{18}$ - $\sqrt{8}$ ）× $\sqrt{2}$ 的结果是．

查看试题解析
14. 甲、乙两人各进行10次射击比赛，平均成绩均为9环，方差分别是：S_甲²＝2，S_乙²＝4，则射击成绩较稳定的是（选填“甲”或“乙”）．

查看试题解析
15. 如图，四边形ABCD是正方形，以AB为一边在正方形外部作等边三角形ABE，连结DE，则 $∠ BED =$ $°$ ．

查看试题解析
16. 已知点A（a，﹣2），B（b，﹣4）在直线y=﹣x+6上，则a、b的大小关系是ab．

查看试题解析
17. 如图平行四边形 ABCD 中，AE ^ BC于E ，AF ^ DC于 F，BC=5，AB=4，AE=3，则 AF的长为．

查看试题解析
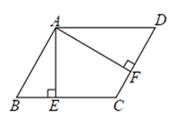18. 如图，已知函数y＝2x+b和y＝ax﹣3的图象交于点P（﹣2，﹣5），则根据图象可得不等式2x+b＞ax﹣3的解集是．

查看试题解析

三、解答题

19. 计算题：

(1)、 $2 \sqrt{12} - 6 \sqrt{\frac{1}{3}} + 3 \sqrt{48}$ ；

(2)、已知x＝ $\sqrt{3}$ ＋1，y＝ $\sqrt{3}$ ﹣1，试求x²＋2xy＋y²的值．

查看试题解析
20. 已知函数y＝(2m＋1)x＋m－3.

(1)、若函数图象经过原点，求m的值

(2)、若函数的图象平行于直线y＝3x－3，求m的值

(3)、若这个函数是一次函数，且y随着x的增大而减小，求m的取值范围．

查看试题解析
21. 如图，四边形ABCD中，AB⊥AD ，已知AD＝3cm ， AB＝4cm ， CD＝12cm ， BC＝13cm ，求四边形ABCD的面积．

查看试题解析
22. 州教育局为了解我州八年级学生参加社会实践活动情况，随机抽查了某县部分八年级学生第一学期参加社会实践活动的天数，并用得到的数据检测了两幅统计图，下面给出了两幅不完整的统计图（如图）

请根据图中提供的信息，回答下列问题：

(1)、a= ，并写出该扇形所对圆心角的度数为，请补全条形图．

(2)、在这次抽样调查中，众数和中位数分别是多少？

(3)、如果该县共有八年级学生2000人，请你估计“活动时间不少于7天”的学生人数大约有多少人？

查看试题解析
23. 已知：如图，在△ABC中，D是BC边上的一点，E是AD的中点，过点A作BC的平行线交于BE的延长线于点F，且AF=DC，连接CF．

(1)、求证：D是BC的中点；

(2)、如果AB=AC，试判断四边形ADCF的形状，并证明你的结论．

查看试题解析
24. 如图，正方形网格中的每个小正方形边长都为1，每个小正方形的顶点叫格点，以格点为顶点分别按下列要求画三角形和平行四边形．

(1)、使三角形三边长为3， $\sqrt{8}$ ， $\sqrt{5}$ ；

(2)、使平行四边形有一锐角为45°，且面积为4．

查看试题解析
25. 在体育局的策划下，市体育馆将组织明星篮球赛，为此体育局推出两种购票方案（设购票张数为x ，购票总价为y）：
方案一：提供8000元赞助后，每张票的票价为50元；

方案二：票价按图中的折线OAB所表示的函数关系确定．

(1)、若购买120张票时，按方案一和方案二分别应付的购票款是多少？

(2)、求方案二中y与x的函数关系式；

(3)、买多少张票时选择方案一和方案二费用相同？

查看试题解析
26. 如图，在平面直角坐标系中，直线 $l_{1}$ ： $y = - \frac{1}{2} x + 6$ 分别与x轴、y轴交于点B、C，且与直线 $l_{2}$ ： $y = \frac{1}{2} x$ 交于点A.

(1)、分别求出点A、B、C的坐标；

(2)、若D是线段 $O A$ 上的点，且 $△ C O D$ 的面积为12，求直线 $C D$ 的函数表达式；

(3)、在（2）的条件下，设P是射线 $C D$ 上的点，在平面内里否存在点Q，使以O、C、P、Q为顶点的四边形是菱形？若存在，直接写出点Q的坐标；若不存在，请说明理由.

查看试题解析