河北省保定市安新县2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2021-04-23 类型:期末考试
一、单选题
-
1. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、2. 函数 的自变量x的取值范围是( )A、 B、 C、 D、3. 甲、乙、丙、丁四人进行射击测试,每人 次射击成绩的平均数均是 环,方差分别为 , , , ,则成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁4. 下列各式,计算结果正确的是( )A、 × =10 B、 + = C、3 - =3 D、 ÷ =35. 下列式子中,表示y是x的正比例函数的是( )A、 B、 C、 D、6. 正方形具备而矩形不一定具备的性质是( )A、四个角都是直角 B、四条边相等 C、对角线相等 D、对角线互相平分7. 直线y=x+1与y=–2x–4交点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 一次中学生田径运动会上,21名参加男子跳高项目的运动员成绩统计如下:
成绩(m)
1.50
1.55
1.60
1.65
1.70
人数
■
8
6
■
1
其中有两个数据被雨水淋混模不清了,则在这组数据中能确定的统计量是()
A、平均数 B、中位数 C、众数 D、方差9. ▱ABCD中,E,F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A、BE=DF B、AE=CF C、AF//CE D、∠BAE=∠DCF10. 若 , ,则 的值为( )A、 B、 C、 D、11. 如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8 m处,发现此时绳子末端距离地面2 m,则旗杆的高度(滑轮上方的部分忽略不计)为( ) A、12 m B、13 m C、16 m D、17 m12. 已知一次函数y=kx+b随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( )A、
A、12 m B、13 m C、16 m D、17 m12. 已知一次函数y=kx+b随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( )A、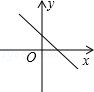 B、
B、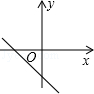 C、
C、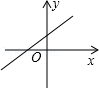 D、
D、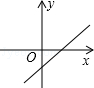 13. 已知林茂的家、体育场、文具店在同一直线上,图中的信息反映的过程是林茂从家跑步去体育场,在体育场锻炼了一阵后又走到文具店买笔,然后再走回家,图中 表示时间, 表示林茂离家的距离。依据图中的信息,下列说法错误的是( )
13. 已知林茂的家、体育场、文具店在同一直线上,图中的信息反映的过程是林茂从家跑步去体育场,在体育场锻炼了一阵后又走到文具店买笔,然后再走回家,图中 表示时间, 表示林茂离家的距离。依据图中的信息,下列说法错误的是( )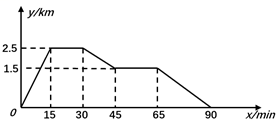 A、体育场离林茂家2.5km B、体育场离文具店1km C、林茂从体育场出发到文具店的平均速度是50m/min D、林茂从文具店回家的平均速度是60m/min14. 如图,矩形ABCD中,连接AC,延长BC至点E,使 ,连接DE.若 ,则∠E的度数是( )
A、体育场离林茂家2.5km B、体育场离文具店1km C、林茂从体育场出发到文具店的平均速度是50m/min D、林茂从文具店回家的平均速度是60m/min14. 如图,矩形ABCD中,连接AC,延长BC至点E,使 ,连接DE.若 ,则∠E的度数是( ) A、65° B、60° C、50° D、40°15. 如图,在△ABC中,点D,E分别是边AB,AC的中点,AF⊥BC,垂足为点F,∠ADE=30°,DF=3,则BF的长为( )
A、65° B、60° C、50° D、40°15. 如图,在△ABC中,点D,E分别是边AB,AC的中点,AF⊥BC,垂足为点F,∠ADE=30°,DF=3,则BF的长为( )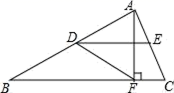 A、4 B、2 C、3 D、416. 如图,矩形 中,对角线 、 相交于点G,E、F分别是边 、 的中点, , ,一动点P从点B出发,沿着 的方向在矩形的边上运动,运动到点C停止.点M为图1中的某个定点,设点P运动的路程为x, 的面积为y,表示y与x的函数关系的图象大致如图2所示.那么,点M的位置可能是图1中的( )
A、4 B、2 C、3 D、416. 如图,矩形 中,对角线 、 相交于点G,E、F分别是边 、 的中点, , ,一动点P从点B出发,沿着 的方向在矩形的边上运动,运动到点C停止.点M为图1中的某个定点,设点P运动的路程为x, 的面积为y,表示y与x的函数关系的图象大致如图2所示.那么,点M的位置可能是图1中的( ) A、点C B、点E C、点F D、点G
A、点C B、点E C、点F D、点G二、填空题
-
17. 如果一组数据:5,x,9,4的平均数为6,那么x的值是18. 尺规作图:作一个角的平分线.
小涵是这样做的:
已知: ,如图1所示
求作:射线 ,使它平分

图1 图2
作法:
⑴如图2,以A为圆心,任意长为半径作弧,交 于点B,交 于点C;
⑵分别以B、C为圆心, 的长为半径作弧,两弧交于点D;
⑶作射线 .
所以射线 就是所求作的射线.
小涵是个喜欢动脑筋的孩子,他继续对图形进行探究:连接 、 和 ,发现 与 的位置关系是 , 依据是 .
19. 正方形 ,正方形 ,正方形 ,按如图所示的方式放置在平面直角坐标系中,若点 、 、 和 、 、 …分别在直线 和x轴上,则点 的坐标是 .
三、解答题
-
20. 计算:(1)、(2)、21. 如图:在平行四边形ABCD中,AM=CN,求证:四边形MBND是平行四边形.
 22. 为了了解学生对“预防新型冠状病毒”知识的掌握情况,学校组织了一次线上知识培训,培训结束后进行测试,试题的满分为 分.为了解学生的成绩情况,从七、八年级学生中各随机抽取了 名学生的成绩进行了整理、描述和分析,下面给出了部分信息:
22. 为了了解学生对“预防新型冠状病毒”知识的掌握情况,学校组织了一次线上知识培训,培训结束后进行测试,试题的满分为 分.为了解学生的成绩情况,从七、八年级学生中各随机抽取了 名学生的成绩进行了整理、描述和分析,下面给出了部分信息:抽取的20名七年级成绩是:
, , , , , , , , , ,
, , , , , , , , , .
抽取的 名八年级成绩折线统计图

抽取的 名学生成绩统计表
性别
七年级
八年级
平均数
众数
中位数
方差
根据以上信息,解答下列问题:
(1)、直接写出上表中a,b,c的值: , , ;(2)、在这次测试中,你认为是七年级成绩好,还是八年级成绩好?请说明理由;23. 如图,学校有一块空地ABCD,准备种草皮绿化已知∠ADC=90°,AD=4米,CD=3米,AB=13米,BC=12米,求这块地的面积. 24. 雄安新区某公司为改善办公条件计划购买A、B两种类型的电脑,已知购买一台A型电脑需要 万元,购买一台B型电脑需要 万元,该公司准备投入资金y万元,全部用于购进 台这两种类型的电脑,设购进A型电脑x台.(1)、求y关于x的函数关系式;(2)、若购进B型电脑的数量不超过A型电脑数量的 倍,则该公司至少需要投入资金多少万元?25. 如图,将矩形纸片ABCD(AD AB)折叠,使点C刚好落在线段AD上,且折痕分别与边BC , AD相交于点E , F , 设折叠后点C , D的对应点分别为点G , H .
24. 雄安新区某公司为改善办公条件计划购买A、B两种类型的电脑,已知购买一台A型电脑需要 万元,购买一台B型电脑需要 万元,该公司准备投入资金y万元,全部用于购进 台这两种类型的电脑,设购进A型电脑x台.(1)、求y关于x的函数关系式;(2)、若购进B型电脑的数量不超过A型电脑数量的 倍,则该公司至少需要投入资金多少万元?25. 如图,将矩形纸片ABCD(AD AB)折叠,使点C刚好落在线段AD上,且折痕分别与边BC , AD相交于点E , F , 设折叠后点C , D的对应点分别为点G , H . (1)、判断四边形CEGF的形状,并证明你的结论;(2)、若AB=4,且四边形CEGF的面积是20,求线段EF的长.26. 如图,一次函数 的图象分别与x轴、y轴相交于点E和点F,点E的坐标为 ,点F的坐标为 ,点A的坐标为 .点P为直线 上的一个动点.
(1)、判断四边形CEGF的形状,并证明你的结论;(2)、若AB=4,且四边形CEGF的面积是20,求线段EF的长.26. 如图,一次函数 的图象分别与x轴、y轴相交于点E和点F,点E的坐标为 ,点F的坐标为 ,点A的坐标为 .点P为直线 上的一个动点. (1)、求直线 的解析式;(2)、若点P在点E、F之间运动(不包含E、F点),求 的面积S与x的函数关系式,并写出自变量x的取值范围;(3)、探究:若点P在直线 上运动,当点P运动到什么位置时, 的面积为 ?
(1)、求直线 的解析式;(2)、若点P在点E、F之间运动(不包含E、F点),求 的面积S与x的函数关系式,并写出自变量x的取值范围;(3)、探究:若点P在直线 上运动,当点P运动到什么位置时, 的面积为 ?