安徽省芜湖市无为市2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2021-04-23 类型:期末考试
一、单选题
-
1. 若式子 有意义,则实数a的取值范围是( )A、a≥﹣2 B、a≠1 C、a>1 D、a≥﹣2且a≠12. 下列计算正确的是( )A、 =﹣3 B、﹣ =﹣0.6 C、 =±6 D、 =3. 五个正整数2、4、5、m、n的平均数是3,且m≠n,则这五个数的中位数是( )A、5 B、4 C、3.5 D、34. 下列各图中,表示y是x的函数的是( )A、
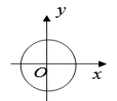 B、
B、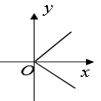 C、
C、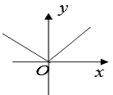 D、
D、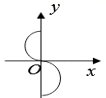 5. 某快递公司快递员六月第三周投放快递物品件数为:有3天是20件,有1天是30件,有3天是40件,这周里日平均投递物品件数为( )A、28件 B、29件 C、30件 D、31件6. 如图,一根长5米的竹竿 斜靠在竖直的墙上,这时 为4米,若竹竿的顶端 沿墙下滑2米至 处,则竹竿底端 外移的距离 ( )
5. 某快递公司快递员六月第三周投放快递物品件数为:有3天是20件,有1天是30件,有3天是40件,这周里日平均投递物品件数为( )A、28件 B、29件 C、30件 D、31件6. 如图,一根长5米的竹竿 斜靠在竖直的墙上,这时 为4米,若竹竿的顶端 沿墙下滑2米至 处,则竹竿底端 外移的距离 ( ) A、小于2米 B、等于2米 C、大于2米 D、以上都不对7. 矩形ABCD的边BC上有一动点E,连接AE、DE,以AE、DE为边作▱AEDF.在点E从点B移动到点C的过程中,▱AEDF的面积( )
A、小于2米 B、等于2米 C、大于2米 D、以上都不对7. 矩形ABCD的边BC上有一动点E,连接AE、DE,以AE、DE为边作▱AEDF.在点E从点B移动到点C的过程中,▱AEDF的面积( ) A、先变大后变小 B、先变小后变大 C、一直变大 D、保持不变8. 若一次函数y=ax+b的图象经过一、二、四象限,则下列不等式中能成立的是( )A、a>0 B、b<0 C、a+b>0 D、a﹣b<09. 勾股定理是人类最伟大的科学发现之一,在我国古算书 《周髀算经》 中早有记载。如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )
A、先变大后变小 B、先变小后变大 C、一直变大 D、保持不变8. 若一次函数y=ax+b的图象经过一、二、四象限,则下列不等式中能成立的是( )A、a>0 B、b<0 C、a+b>0 D、a﹣b<09. 勾股定理是人类最伟大的科学发现之一,在我国古算书 《周髀算经》 中早有记载。如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )
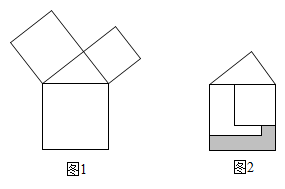 A、直角三角形的面积 B、最大正方形的面积 C、较小两个正方形重叠部分的面积 D、最大正方形与直角三角形的面积和10. 如图,平面直角坐标系中,在边长为1的正方形 的边上有—动点 沿正方形运动一周, 则 的纵坐标 与点 走过的路程 之间的函数关系用图象表示大致是( )
A、直角三角形的面积 B、最大正方形的面积 C、较小两个正方形重叠部分的面积 D、最大正方形与直角三角形的面积和10. 如图,平面直角坐标系中,在边长为1的正方形 的边上有—动点 沿正方形运动一周, 则 的纵坐标 与点 走过的路程 之间的函数关系用图象表示大致是( ) A、
A、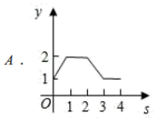 B、
B、 C、
C、 D、
D、
二、填空题
-
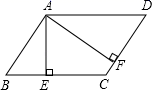
11. 如图,在平行四边形ABCD中,AE⊥BC于点E , AF⊥CD于点F , 若∠EAF=70°,则∠B的度数为 .
 12. 如果将直线y=3x平移,使其经过点(0,﹣1),那么平移后的直线表达式是 .13. 已知x= +1,则x2﹣2x﹣3= .14. 在△ABC中,∠B=∠C=30°,AB=2 ,点D在BC边上,连接AD , 若△ABD为直角三角形,则线段BD的长为 .
12. 如果将直线y=3x平移,使其经过点(0,﹣1),那么平移后的直线表达式是 .13. 已知x= +1,则x2﹣2x﹣3= .14. 在△ABC中,∠B=∠C=30°,AB=2 ,点D在BC边上,连接AD , 若△ABD为直角三角形,则线段BD的长为 .三、解答题
-
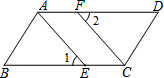
15. 计算:( +1)2﹣ +2 .16. 已知,如图,E、F分别为▱ABCD的边BC、AD上的点,且∠1=∠2,.求证:AE=CF.
 17. 如图,在四边形ABCD中,AB=13,BC=3,CD=4,DA=12,∠ADB=90°,求四边形ABCD的面积.
17. 如图,在四边形ABCD中,AB=13,BC=3,CD=4,DA=12,∠ADB=90°,求四边形ABCD的面积. 18. 已知线段 ,直线 垂直平分 且交 于点 .以 为圆心, 长为半径作弧,交直线 于 两点,分别连接 .
18. 已知线段 ,直线 垂直平分 且交 于点 .以 为圆心, 长为半径作弧,交直线 于 两点,分别连接 . (1)、根据题意,补全图形;(2)、求证:四边形 为正方形.19. 在一条东西走向河的一侧有一村庄 ,河边原有两个取水点 ,其中 ,由于某种原因,由 到 的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点 在同一条直线上),并新修一条路 ,测得 千米, 千米, 千米.
(1)、根据题意,补全图形;(2)、求证:四边形 为正方形.19. 在一条东西走向河的一侧有一村庄 ,河边原有两个取水点 ,其中 ,由于某种原因,由 到 的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点 在同一条直线上),并新修一条路 ,测得 千米, 千米, 千米.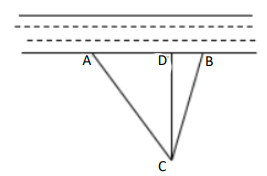 (1)、问 是否为从村庄 到河边最近的路?请通过计算加以说明:(2)、求原来的路线 的长.20. 某市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了四次测试,测试成绩如表(单位:环):
(1)、问 是否为从村庄 到河边最近的路?请通过计算加以说明:(2)、求原来的路线 的长.20. 某市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了四次测试,测试成绩如表(单位:环):第一次
第二次
第三次
第四次
甲
9
8
8
7
乙
10
6
7
9
(1)、根据表格中的数据,分别计算甲、乙两名运动员的平均成绩;(2)、分别计算甲、乙两人四次测试成绩的方差;根据计算的结果,你认为推荐谁参加省比赛更合适?请说明理由.21. 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如: ,善于思考的小明利用完全平方公式进行了以下探索:.请你仿照小明的方法解决下列问题:
(1)、 ,则 , ;(2)、已知 是 的算术平方根,求 的值;(3)、当 时,化简 .22. 某学校为了防控新型冠状病毒,购买了甲、乙两种消毒液进行校园环境消毒.已知学校第一次购买了甲种消毒液40瓶和乙种消毒液60瓶,共花费3 600元;第二次购买了甲种消毒液60瓶和乙种消毒液40瓶,共花费3 400元.(1)、每瓶甲种消毒液和每瓶乙种消毒液的价格分别是多少元?(2)、学校准备第三次购买这两种消毒液,其中甲种消毒液比乙种消毒液多10瓶,并且总花费不超过3 500元,最多能购买多少瓶甲种消毒液?23. 如图,在平行四边形 中, 的平分线交 于点E,交 的延长线于F,以 为邻边作平行四边形 。 (1)、证明平行四边形 是菱形;(2)、若 ,连结 ,①求证: ;②求 的度数;(3)、若 , , ,M是 的中点,求 的长。
(1)、证明平行四边形 是菱形;(2)、若 ,连结 ,①求证: ;②求 的度数;(3)、若 , , ,M是 的中点,求 的长。