安徽省合肥市肥东县2019-2020学年八年级下学期数学期末试卷
试卷更新日期：2021-04-23 类型：期末考试
一、单选题
-
1. 计算的结果是（ ）A、6 B、 C、2 D、2. 一元二次方程 的根是（ ）A、 B、 C、 ， D、无实数根3. 某同学对甲、乙、丙、丁四个市场五月份每天的白菜价格进行调查，计算后发现这个月四个市场的白菜价格的平均数相同，方差分别为s甲2=10，s乙2=8.2，s丙2=6.5，s丁2=2.6，则五月份白菜价格最稳定的市场是（ ）A、甲 B、乙 C、丙 D、丁4. 如果一个多边形的每个外角都等于36°，那么这个多边形的边数是（ ）A、12 B、10 C、8 D、65. 如果关于x的一元二次方程ax2+x-1=0有两个不相等的实数根，则a的取值范围是（ ）A、a＞- B、a≥- C、a≥- 且a≠0 D、a＞- 且a≠06. 如图，在行距、列距都是1的4×4的方格网中，将任意连接两个格点的线段称作“格点线”，则“格点线”的长度不可能等于（ ）
A、 B、 C、 D、7. 某商品经过连续两次降价，售价由原来的每件25元降到每件16元，则平均每次降价的百分率为（ ）．A、20% B、40% C、18% D、36%8. 平行四边形ABCD各边中点依次是E、F、G、H，关于四边形EFGH，下面结论一定成立的是（ ）A、有一个内角等于90° B、有一组邻边相等 C、对角线互相垂直 D、对角线互相平分9. 已知a、b是方程x2-2x-1=0的两根，则a2+a+3b的值是（ ）A、7 B、5 C、-5 D、-710. 如图，矩形ABCD的对角线AC、BD交于点O，点P在边AD上从点A到点D运动，过点P作PE⊥AC于点E，作PF⊥BD于点F，已知AB=3，AD=4，随着点P的运动，关于PE+PF的值，下面说法正确的是（ ）
A、先增大，后减小 B、先减小，后增大 C、始终等于2.4 D、始终等于3二、填空题
-
11. 如果最简二次根式 和 是同类二次根式，那么a=12. 如图，在△ABC中，点M在边AB上，点N在边AC上，AM=BM，且MN//BC，如果MN=5，那么BC= ．
13. 李明同学进行射击练习，两发子弹各打中5环，四发子弹各打中8环，三发子弹各打中9环．一发子弹打中10环，则他射击的平均成绩是环．14. 已知一个菱形的两条对角线的长分别为5cm和8cm，该菱形的面积为cm2 ．15. 观察分析下列数据：0，－ ， ，－3，2 ，－ ，3 ，…，根据数据排列的规律得到第16个数据应是 ． (结果需化简)16. 如图，正方形ABCD中，点E在边BC上，∠BAE=n°．如果在边AB、CD上分别找一点F、G，使FG=AE，FG与AE相交于点O，那么∠GOE的大小等于 ．
三、解答题
-
17. 计算：18. 用公式法解方程：x2+4x-5=019. 如图，已知等腰三角形ABC的底边BC=20cm，D是腰AB上的一点，且BD=12cm，CD=16cm．
(1)、求证：△BCD是直角三角形；(2)、求△ABC的周长．20. 合肥百货大楼服装柜在销售发现：某童装平均每天可售出20件，每件盈利40元．为了迎接“六•一”儿童节，商场决定采取适当的降价措施，扩大销售量，增加盈利，尽快减少库存．经市场调查发现：如果每件童装降价2元，那么平均每天就可多售出4件．要想平均每天销售这种童装盈利1200元，那么每件童装应降价多少元？21. 为弘扬中华传统文化，某校组织八年级1000名学生参加汉字听写大赛，为了解学生整体听写能力，赛后随机抽查了部分学生的成绩（得分取正整数，满分为100分）进行统计分析，并制作成图表：组别
一
二
三
四
五
分数段
50.5～60.5
60.5～70.5
70.5～80.5
80.5～90.5
90.5～100.5
频数
16
30
m
80
24
频率
0.08
0.15
0.25
n
0.12
(1)、本次抽样调查的样本容量为 ， 表中m= ． n；(2)、此样本中成绩的中位数落在第组内；(3)、补全频数分布直方图；(4)、若成绩超过80分为优秀，请你估计该校八年级学生中汉字听写能力优秀的人数．22. 如图，在Rt△ABC中，∠ACB＝90°，过点C的直线MN∥AB ， D为AB边上一点，过点D作DE⊥BC ， 交直线MN于E ， 垂足为F ， 连接CD、BE ．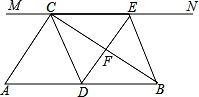
(1)、求证：CE＝AD；(2)、当D在AB中点时，四边形BECD是什么特殊四边形？说明你的理由；(3)、若D为AB中点，则当∠A的大小满足什么条件时，四边形BECD是正方形？请说明你的理由．