安徽省当涂县2019-2020学年八年级下学期数学期末试卷

试卷更新日期：2021-04-23 类型：期末考试

进入出卷网下载

一、单选题

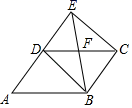
1. 正五边形的每一个内角是（）

A、 $30 °$ B、 $72 °$ C、 $108 °$ D、 $120 °$

查看试题解析
2. 若代数式 $\sqrt{x - 1}$ 在实数范围内有意义，则 $x$ 的取值范围是 $($ $)$

A、x<1 B、x≤1 C、x>1 D、x≥1

查看试题解析
3. 下列根式不能与 $\sqrt{3}$ 合并的是（）

A、 $\sqrt{12}$ B、 $- \sqrt{18}$ C、 $\sqrt{27}$ D、 $- \sqrt{75}$

查看试题解析
4. 一元二次方程 $x^{2} - 2 x + 1 = 0$ 的根的情况是（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
5. 下列等式成立的是（）

A、 $\sqrt{9} - \sqrt{4} = 5$ B、 $\sqrt{5} + \sqrt{3} = 2 \sqrt{2}$ C、 $\sqrt{9} = \pm 3$ D、 $\sqrt{{(- 9)}^{2}} = 9$

查看试题解析
6. 如图，E是 $▱ A B C D$ 边 $A D$ 延长线上一点，连接 $B E$ ， $C E$ ， $B D$ ， $B E$ 交 $C D$ 于点F．添加以下条件，不能判定四边形 $B C E D$ 为平行四边形的是（）

A、 $∠ A B D = ∠ D C E$ B、 $D F = C F$ C、 $∠ A E B = ∠ B C D$ D、 $∠ A E C = ∠ C B D$

查看试题解析
7. 某机械厂一月份生产零件50万个，第一季度生产零件200万个．设该厂二、三月份平均每月的增长率为x，那么x满足的方程是（）

A、 $50 {(1 + x)}^{2} = 200$ B、 $50 + 50 {(1 + x)}^{2} = 200$ C、 $50 + 50 (1 + x) + 50 {(1 + x)}^{2} = 200$ D、 $50 + 50 (1 + x) + 50 (1 + 2 x) = 200$

查看试题解析
8. 下列命题中，真命题是（）

A、两条对角线相等的四边形是矩形 B、两条对角线互相垂直的四边形是菱形 C、两条对角线互相垂直且相等的四边形是正方形 D、两条对角线互相平分的四边形是平行四边形

查看试题解析
9. 已知a，b，c是 $Δ A B C$ 的三边长，且满足 $\sqrt{a - 6} + | b - 8 | + {(c - 10)}^{2} = 0$ ，则 $Δ A B C$ 是（）

A、以a为斜边的直角三角形 B、以b为斜边的直角三角形 C、以c为斜边的直角三角形 D、以c为底边的等腰三角形

查看试题解析
10. 如图，点E在正方形 $A B C D$ 的边 $A B$ 上，若 $E B = 1$ ， $E C = 3$ ，那么正方形 $A B C D$ 的面积为（）

A、 $2 \sqrt{2}$ B、8 C、 $\sqrt{10}$ D、10

查看试题解析

二、填空题

11. 若 $\sqrt{{(x - 3)}^{2}} = 3 - x$ ，则x的取值范围是．

查看试题解析
12. 一组数据 $- 2$ ，1，1，0，2，1，这组数据的中位数和众数分别是和．

查看试题解析
13. 一元二次方程 ${(x + 1)}^{2} = x + 1$ 的根是．

查看试题解析
14. 已知m是方程 $x^{2} - 2 x - 1 = 0$ 的一个根，且 $3 m^{2} - 6 m + a = 8$ ，则a的值等于．

查看试题解析
15. 样本容量为 80，共分为六组，前四个组的频数分别为 12，13，15，16，第五组的频率是 0.1，那么第六组的频率是．

查看试题解析
16. 关于x的一元二次方程（k-1）x²-2x+1=0有两个不相等的实数根，则实数k的取值范围是．

查看试题解析
17. 在 $Δ A B C$ 中， $A C = 3$ ， $B C = 4$ ， $A B = 5$ ，则 $A B$ 边上的高是．

查看试题解析
18. 矩形的一条边长为 $2 cm$ ，且两条对角线夹角为 $60 °$ ，则矩形的周长为．

查看试题解析

三、解答题

19.

(1)、计算： $\sqrt{32} \div \sqrt{2} - \sqrt{\frac{1}{2}} \times \sqrt{12} \div \sqrt{24}$ ；

(2)、解方程： $x^{2} + x - 1 = 0$ ．

查看试题解析
20. 若一元二次方程 $x^{2} - x = 1$ 的两个实数根分别为 $x_{1}$ ， $x_{2}$ ，求 $(x_{1} - 1) (x_{2} - 1)$ 的值．

查看试题解析
21. 如图，在□ $A B C D$ 中，E、F分别是 $A B$ ， $C D$ 边上的点，且 $∠ A D E = ∠ C B F$ ．当 $B D ⊥ E F$ 时，求证：四边形 $E B F D$ 是菱形．

查看试题解析

22. 某省射击队为从甲、乙两名运动员中选拔一人参加全国比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：

	第一次	第二次	第三次	第四次	第五次	第六次
甲	9	8	9	8	10	10
乙	9	7	10	10	8	10

(1)、根据表格中的数据，计算出甲的平均成绩是环，乙的平均成绩是环；

(2)、分别计算甲、乙六次测试成绩的方差；

(3)、根据（1）、（2）计算的结果，从发挥的稳定性看，你认为推荐谁参加全国比赛更合适，请说明理由．

查看试题解析

23. 今年我国发生了较为严重的新冠肺炎疫情，口罩供不应求．某商店恰好年前新进了一批口罩，若按每个盈利1元销售，每天可售出200个，如果每个口罩的售价上涨0.5元，则销售量就减少10件，问应将每件涨价多少元时，才能让顾客得到实惠的同时每天利润为480元？

查看试题解析
24. 如图，矩形 $A B C D$ 中， $A B =3$ ， $B C =4$ ，E为 $A D$ 中点，F为 $C D$ 上一点，将 $Δ D E F$ 沿 $E F$ 折叠后，点D恰好落到 $B F$ 上的点G处．

(1)、连接 $B E$ ，求证： $B E ⊥ E F$ ；

(2)、求折痕 $E F$ 的长．

查看试题解析