安徽合肥市瑶海区2019-2020学年八年级下学期数学期末试卷

试卷更新日期：2021-04-23 类型：期末考试

进入出卷网下载

一、单选题

1. 要使 $\sqrt{x - 2020}$ 有意义，x的取值范围是（）

A、x≥2020 B、x≤2020 C、x> 2020 D、x< 2020

查看试题解析
2. 下列计算，正确的是（）

A、 $\sqrt{8} + \sqrt{3} = \sqrt{11}$ B、 $\sqrt{9} \div \sqrt{3} = 3$ C、 $\sqrt{18} - \sqrt{2} = 2 \sqrt{2}$ D、 $\sqrt{9 \frac{1}{4}} = 3 \frac{1}{2}$

查看试题解析
3. 下列方程中，关于x的一元二次方程是（）

A、x²﹣x（x+3）＝0 B、ax²+bx+c＝0 C、x²﹣2x﹣3＝0 D、x²﹣2y﹣1＝0

查看试题解析
4. 下列方程中，没有实数根的是（）

A、3x²- $\sqrt{3}$ x+2=0 B、4x²+4x+1=0 C、x²-3x-4=0 D、 $\sqrt{3}$ x²-x-1=0

查看试题解析
5. 如图，在数轴上点A所表示的数为a，则a的值为（）

A、 $- 1 - \sqrt{5}$ B、 $1 - \sqrt{5}$ C、 $- \sqrt{5}$ D、 $- 1 + \sqrt{5}$

查看试题解析
6. 盛夏来袭，为促进消费，瑶海万达广场从6月份开始对部分商品进行“折上折”（两次打折数相同）优惠活动，已知一件原价1000元的服装，优惠后实际仅需640元，设该服装原本打x折，则有（）

A、1000(1-2x)=640 B、1000(1-x)²=640 C、1000 ${(\frac{x}{10})}^{2}$ =640 D、1000 ${(1 - \frac{x}{10})}^{2}$ =640

查看试题解析
7. 如图，在 $Δ A B C$ 中， $D ， E$ 分别是 $A B ， B C$ 的中点，点F在 $D E$ 延长线上，添加一个条件使四边形 $A D F C$ 为平行四边形，则这个条件是（）

A、 $∠ B = ∠ F$ B、 $∠ B = ∠ B C F$ C、 $A C = C F$ D、 $A D = C F$

查看试题解析
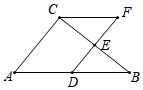8. 小梅每天坚持背诵英语单词，她记录了某一周每天背诵英语单词的个数，如下表：

星期

日

一

二

三

四

五

六

个数

11

12

13

10

13

13

其中有一天的个数被墨汁覆盖了，但小梅已经计算出这组数据唯一众数是13，平均数12，那么这组数据的方差是（）

A、 $\frac{8}{7}$ B、 $\frac{10}{7}$ C、1 D、 $\frac{9}{7}$

查看试题解析
9. 如图，在四边形ABCD中，AB=BC=CD，∠ABC=160°，∠BCD=80°，△PDC为等边三角形，则∠ADC的度数为（）

A、70° B、75° C、80° D、85°

查看试题解析
10. 对于实数a、b，定义运算“★”：a★b= ${\begin{array}{l} a^{2} - b (a \leq b) \\ b^{2} - a (a > b) \end{array}$ ，关于x的方程（2x+1）★（2x-3）=t恰好有两个不相等的实数根，则t的取值范围是（）

A、t＜ $\frac{15}{4}$ B、t＞ $\frac{15}{4}$ C、t＜ $- \frac{17}{4}$ D、t＞ $- \frac{17}{4}$

查看试题解析

二、填空题

11. 如果最简二次根式 $\sqrt{1 +a}$ 与 $\sqrt{4 a - 2}$ 是同类二次根式，那么a=.

查看试题解析
12. 已知 $x_{1}$ 、 $x_{2}$ 是方程 $x^{2} + x - 2 = 0$ 的两个根，则 $\frac{1}{x_{1}} + \frac{1}{x_{2}} =$ .

查看试题解析
13. 如图，每个小正方形边长为1，则△ABC边AC上的高BD的长为.

查看试题解析
14. 已知平行四边形ABCD的四个顶点都在某一个矩形上，其中BD为这个矩形的对角线，若AB=2，BC=3，∠ABC=60°，则这个矩形的周长是

查看试题解析

三、解答题

15. 计算：（2 $\sqrt{12}$ - $\sqrt{\frac{1}{3}}$ ）× $\sqrt{6}$

查看试题解析
16. 解方程：x²+x=8-x

查看试题解析
17. 已知关于x的一元二次方程ax²+bx+ $\frac{1}{2}$ =0

(1)、若x=1是方程的一个解，写出a、b满足的关系式；

(2)、当b=a+1时，利用根的判别式判断方程根的情况．

查看试题解析
18. 著名数学家斐波那契曾研究一列数，这列数的第n个数为 $\frac{1}{\sqrt{5}} [{(\frac{1 + \sqrt{5}}{2})}^{n} - {(\frac{1 - \sqrt{5}}{2})}^{n}]$ （n为正整数），例如这列数的第8个数可以表示为 $\frac{1}{\sqrt{5}} [{(\frac{1 + \sqrt{5}}{2})}^{8} - {(\frac{1 - \sqrt{5}}{2})}^{8}]$ ，根据以上材料，写出并计算这列数的第2个数．

查看试题解析
19. 《九章算术》“勾股”章有一题：“今有二人同所立，甲行率七，乙行率三．乙东行，甲南行十步而斜东北与乙会．问甲乙行各几何”．大意是说，已知甲、乙二人同时从同一地点出发，甲的速度为7，乙的速度为3．乙一直向东走，甲先向南走10步，后又斜向北偏东方向走了一段后与乙相遇．那么相遇时，甲、乙各走了多远？

查看试题解析
20.

(1)、已知线段a、以此为边，用尺规作图（保留作图痕迹，不需写作法）作出一个含有60°的菱形；

(2)、如图，在菱形ABCD中，点M、N分别是边BC、CD上的点，连接AM、AN，若∠ABC=∠MAN=60°，求证：BM=CN；

查看试题解析

21. 疫情防控期间，学生居家锻炼受到一定限制，不能达到室外锻炼的效果，有些同学存在体能下降的现象．瑶海区某校八年级甲、乙两班各50名学生，为了了解这两个班学生身体素质情况，进行了抽样调查，从这两个班各随机抽取10名学生进行身体素质测试，测试成绩如下：

甲班：65 75 75 80 60 50 75 90 85 65；

乙班：90 55 80 70 55 70 95 80 65 70；

整理上面数据，得到如下统计表：

	50≤x＜60	60≤x＜70	70≤x＜80	80≤x＜90	90≤x≤100
甲班	1	3	3	2	1
乙班	2	1	3	2	2

样本数据的平均数、众数、中位数如下表所示：

	平均数	中位数	众数
甲班	m	75	75
乙班	73	70	n

根据以上信息，解答下列问题：

(1)、求表中m的值；

(2)、表中n的值为；

(3)、若规定测试成绩在80分以上（含80分）的学生身体素质为优秀，请估计乙班50名学生中身体素质为优秀的学生的人数．

查看试题解析

22. 合肥长江180艺术街区进行绿化改造，用一段长40m的篱笆和长15m的墙AB，围城一个矩形的花园，设平行于墙的一边DE的长为xm；

(1)、如图1，如果矩形花园的一边靠墙AB，另三边由篱笆CDEF围城，当花园面积为150m²时，求x的值；

(2)、如图2，如果矩形花园的一边由墙AB和一节篱笆BF构成，另三边由篱笆ADEF围城，当花园面积是150m²时，求BF的长．

查看试题解析
23. 如图1，正方形ABCD的顶点A、D分别在平行线l₁、l₂上，由B、D向l₁作垂线，垂足分别为M、N．

(1)、求证：AM=DN；

(2)、如图2，正方形AEFG的顶点E在直线l₂上，过点F、C分别作l₂的垂线段FP、CQ，求证：FP+CQ=DE；

(3)、如图3，正方形AEFG的顶点A、G在直线l₁上，顶点E、F在直线l₂上，连接BG并延长交l2于点R，若∠BRD=30°，AE= $\sqrt{3}$ ，求AB．

查看试题解析

星期	日	一	二	三	四	五	六
个数	11	12		13	10	13	13